작성자 : 유기선

1.Introduction

시계열 분석은 기상 예측 , 모니터링 데이터의 이상 감지 및 행동 인식을 위한 궤적 분류 와 같은 다양한 실제 응용 분야에서 널리 사용되며, 이러한 넓은 실용적 가치 때문에 시계열 분석은 큰 관심을 받고 있다.

일반적으로 언어나 비디오와 같은 다른 유형의 순차 데이터와 달리 시계열은 연속적으로 기록되며 각 시간 지점은 일부 스칼라만 저장한다. 그러나 하나의 단일 시간 지점으로는 보통 분석에 충분한 의미적 정보를 제공할 수 없기 때문에, 많은 경우 더 많은 정보를 제공하기 위해 시계열의 내재적인 특성인 연속성, 주기성, 추세 등을 반영할 수 있는 시간적 변화에 초점을 맞추고 있다. 그러나 실제 시계열의 변동은 항상 복잡한 시간 패턴을 포함하며, 여러 변동(상승, 하강, 변동 등)이 서로 섞이고 중첩되어 모델링을 매우 어렵게 만든다. 특히 딥러닝 커뮤니티 에서는 이런 복잡한 시계열 Data 의 시간적 변화를 포착하기 위해, (RNN), (TCN), Attention 메커니즘 을 사용하여 모델링을 진행하고 있으나, 각 모델들의 한계로 인해 효율적인 모델링을 진행하는데 한계가 존재한다.

본 논문에서는, 복잡한 시간적 변동을 해결하기 위해 시계열 데이터를 다양한 주기성에서 분석한다. 실제 현실세계의 시계열 데이터는 일일, 주간, 연간 같은 주기성을 관찰할 수 있으며, 이런 주기성이 서로 상호작용하여 변동 모델링을 어렵게 한다.

이 관점에서 해당 논문의 핵심은 이런 시계열 데이터를 주기내에서의 변동성 (intraperiod-variation) 과 주기 간 변동성(interperiod-variation) 으로 각각 나눠, 기존 Temporal Variation 을 Intraperiod - , Interperiod – variation 으로 확장하여 Multi – periodicity 특성을 반영하는 것이다.

이런 Multi – periodicity 특성을 반영하기 위해, 1D 시계열을 2D 공간으로 확장한다. 구체적으로, 그림 1처럼, 1D 시계열을 각 열이 주기 내 시간 점을 포함하고 각 행이 서로 다른 주기에서 동일한 위상의 시간 점을 포함하는 2D 텐서로 재구성 한다. 따라서 1D 시계열을 2D 텐서 집합으로 변환하여 원래의 1D 공간에서 표현 능력 병목 현상을 깨고 2D 공간에서 intra-period- 및 inter-period-variations를 효과적으로 통합하여 시간적 2D-variations을 얻을 수 있다.

또한 기술적으로, 위와 같은 동기에 기반하여, 이전 백본(backbone)을 넘어서 시계열 분석을 위한 새로운 태스크-일반 모델로 TimesNet을 제안한다.

구체적으로, TimesBlock은 학습된 주기를 기반으로 1D 시계열을, 2D 텐서 SET 으로 변환하고, 파라미터 효율적인 inception block 을 통해 2D 공간에서 intra-period 및 inter-period 변화를 포착할 수 있다. 실험적으로, TimesNet 은 단기 및 장기 예측, 대체, 분류 및 이상 탐지를 포함한 5 가지 주요 분석 작업에서 일관된 최고 성능을 달성했다.

2.RELATED WORK

시계열 분석의 주요 문제인 시간적 변화 모델링은, ARIMA(Anderson & Kendall, 1976), Holt-Winter(Hyndman & Athanasopoulos, 2018) 및 Prophet(Taylor & Letham, 2018) 같은 고전적 모델 기반의 연구가 진행되었으나, 시계열의 변화는 일반적으로 미리 정의된 패턴으로는 충분히 설명하기 어렵기 때문에 실용성은 제한되는 한계가 존재했다.

최근 에는 MLP, TCN, RNN 기반의 다양한 Deep 모델들이 시계열 모델링에 적용되 왔다. 우선 MLP 기반의 방법들 (Oreshkin et al., 2019; Challu et al., 2022; Zeng et al., 2023; Zhang et al., 2022)은 MLP을 시간 축으로 사용하며, 시간 의존성을 MLP 레이어의 고정된 파라미터로 인코딩 한다. TCN 기반의 방법 (2019)은 시간 축을 따라 이동하는 컨볼루션 커널로 시간 변화를 캡쳐하며, RNN 기반의 방법 (Hochreiter & Schmidhuber, 1997; Lai et al., 2018; Gu et al., 2022)은 재귀 구조를 활용하며, 시간 단계 간 상태 전이를 통해 시간 변화를 캡쳐한다. 특히 최근 딥러닝 분야에서 전반적으로 높은 성능을 보이는 Transformer는 시계열 예측에서도 큰 성능을 보여주고 있으며 (Zhou et al., 2021; Liu et al., 2021a; Wu et al., 2021; Zhou et al., 2022), 어텐션 메커니즘을 사용하여 시간 포인트 간의 시간적 종속성을 파악할 수 있다. 특히, Wu et al.은 학습된 주기를 기반으로 자기 상관 메커니즘을 갖춘 Autoformer를 제시 했으며. 그 후, FEDformer (Zhou et al., 2022)는 계절성-추세 분해를 강화하고 주파수 도메인 내에서 sparse 어텐션을 제시했다. 그러나 본 논문의 경우 이전 방법과 달리, 시계열의 다중 주기성을 탐색하여 복잡한 시간적 패턴을 해결하고, 이미 인공지능 컴퓨터 비전에서 잘 알려진 백본을 사용하여 처음으로 2D 공간에서 시간적 2D-변화를 포착한다.

3.TIMESNET

해당 논문을 이해하기 위해서 우선 Multi periodicity 를 이해해야 한다. Multi periodicity 는 위에서 간단히 언급했지만, 해당 논문은 Intraperiod Variation과 Intreperiod Variation 을 구분하여 분석하였다. 우선 Intraperiod Variation 은 Period 내에서 발생하는 Variation 으로 Short Term Temporal pattern 을 반영하며, 일반적으로 1D Time Series data 를 Input 으로 모델링 진행시 고려하는 Variation 이다. 또한 추후 2D Tensor 로 변환할 때 각 Column 으로 표현되어 같은 Period 내 time Point 간의 Variation 을 의미한다. 반면 Interperiod Variation 은 서로 다른 Period 에서 발생하는 Variation 으로 Long Term Temporal Pattern 을 반영한다. 이는 2D Tensor 로 변환시 각 row 로 표현되어 다른 Period 에 존재하지만, 같은 Phase 를 가지는 time points 간 Temporal Variation 을 의미한다. 이 논문은 이 둘을 조합하여 사용 하는 것이 key idea 이다.

여기서 Interperiod 의 기준을 나누기 위해서 그림 1과 같이 해당 Data 에서 다양한 Period 를 얻어야 한다. 이를 위하해서 해당 논문은 아래 그림과 식처럼 Fast Fourier Transform 을 사용한다.

FFT 를 적용해서 Sequence 에 대한 Amplitude 및 Frequency 를 도출 하고, Frequency 중 Amplitude 값이 가장 높은 Top K 개의 Frequency 를 선정하여, Frequency 에 상응하는 Period 를 구한다. 여기서 top K 개의 Frequency 를 선정하는 이유는 Frequency 영역의 sparse 함을 고려했을때, 으미 없는 high Frequency 에 의한 Nosie 를 피하기 위한것이다.

여기서 선정된 Top K개의 Frequency 에 해당하는 Period 는 위 수식에서 pi 로 설정한다. 이렇게 구해진 Frequency {f1, …, fk} 와Period {p1, …, pk} 를 이용하여 1D Time series data 를 2D Tensor 로 변환 한다. 여기서 Padding 은 2D tensor 로 재구성 하기 위해 시계열을 시간 축을 따라 0으로 패딩하는 작업인데, 아래 수식 에서 T/fi 값을 맞춰주기 위해 진행한다. (pi와 fi는 각각 i번째 변환된 2D 텐서의 행과 열의 수를 나타낸다.) 이와 같은 방식으로 선택된 주파수와 추정된 주기에 기반하여 k개의 다른 2D 변동을 나타내는 2D 텐서 집합 을 얻게 된다. 이러한 변환은 변환된 2D 텐서에 두 가지 유형의 지역성(locality)을 가져다 준다는 점도 주목할 만하다. 즉, 연속된 시간점(열, intra-period variation)과 인접한 주기(행, inter-period variation) 사이의 지역성이다. 따라서, 시계열 2D-변동성은 2D 커널에 의해 쉽게 처리될 수 있다.

3.2.TIMESBLOCK

Capturing temporal 2D-variation

위 그림처럼 Reshape 된 결과를 통해 pi, fi 에 대한 Representation 을 추출한다. 여기서 input 은 이고 output 은 이다. 또한 위의 그림처럼 Reshape Back 이라는 과정을 통해 Convolution 과정을 통해 추출한 Representation 을 다시 기존 형태로 Reshape 을 하게 된다.

마지막으로 아래 식처럼 Adaptive Aggregation 을 수행하게 되는데, 이는 이전 과정을 통해 만들어진 1D time series data 를 Aggregation 하는 과정이다. Amplitude A 는 선택된 Top K 개의 Frequency 와 Period 간 상대적 중요도를 반영할 수 있으므로, Transform 된 Tensor 의 중요도 역시 반영할 수 있다. 이로부터 처음 FFT 과정을 통해 구해진 Amplitude 값을 바탕으로 Aggregation 하게 된다. 이로부터 나온 결과는 서로 다른 Period 간 Interperiod, Intraperiod variation 을 고려한 Temporal 2D Variation 을 동시에 캡쳐한 결과를 얻을 수 있다.

4.EXPERIMENTS

TimesNet의 일반성을 검증하기 위해, 장/단기 예측, 보완, 분류 및 이상 탐지의 다섯 가지 주요 분석 작업에 대한 실험을 진행함.

• 위 표 1은 벤치마크의 평가 결과 Summary-

-BaseLine

• 이에는 RNN 기반 모델인 LSTM (1997), LSTNet (2018) 및 LSSL (2022); CNN 기반 모델인 TCN (2019); MLP 기반 모델인 LightTS (2022) 및 DLinear (2023); Transformer 기반 모델인 Reformer (2020), Informer (2021), Pyraformer (2021a), Autoformer (2021), FEDformer (2022), Non-stationary Transformer (2022a) 및 ETSformer (2022) 등이 포함됨. 또한 각각의 특정 작업에 대해 최신 기법인 N-HiTS (2022)와 N-BEATS (2019)를 사용한 단기 예측, 이상 탐지를 위한 Anomaly Transformer (2021), 분류를 위한 Rocket (2020)과 Flowformer (2022) 등과 같은 최신 모델들과도 비교함. 종합적인 비교를 위해 15개 이상의 기준 모델을 포함하였음.

-4.1 주요결과

TimesNet은 위 그림과 같이 5개 Mainstream Task 에서 다른 모델들 대비 모든 방면에서 SOTA 를 달성하였다. 또한 인셉션 블록을 더 강력한 비전 백본으로 대체함으로써 TimesNet의 성능을 더욱 향상시킬 수 있음을 보인다. (위 그림의 오른쪽)

**-4.1 단기 및 장기 예측 설정 **

시계열 예측은 날씨 예보, 교통 및 에너지 소비 계획에 필수적이며, 이러한 예측 모델의 성능을 평가하기 위해, 장/단기 예측을 포함한 두 가지 유형의 벤치마크로 비교함.

• 장기 예측: Autoformer (2021)에서 사용한 벤치 사용.
• 단기 예측: M4 (Spyros Makridakis, 2018)를 채택
  • 연간, 분기 및 월별로 수집된 단일 변수 마케팅 데이터 포함.

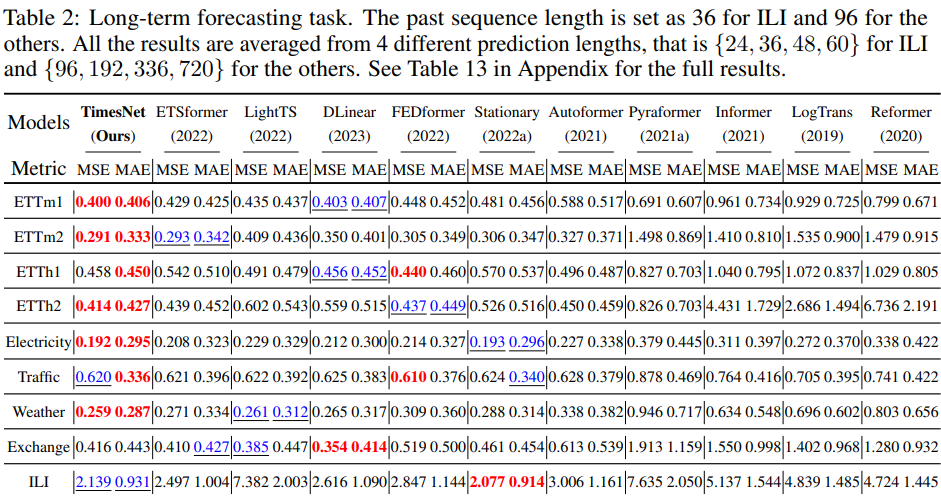
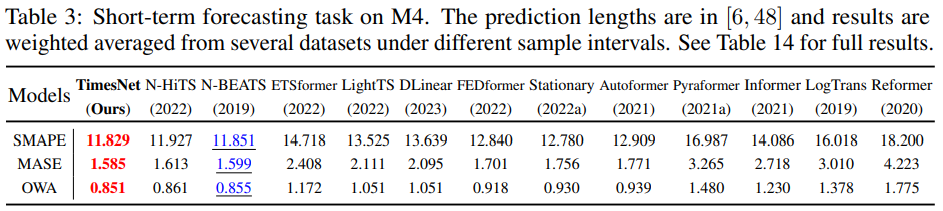
- 결과

TimesNet은 장기 및 단기 설정에서 뛰어난 성능을 보여줍니다 (표 2-3). 표13 에서 TimesNet의 장기 예측의 경우 80% 이상의 경우에서 SoTA 달성함. M4 데이터셋의 경우, 시계열이 다른 소스에서 수집되기 때문에 시간적 변동이 매우 커져, 이로 인해 예측이 훨씬 어려질 수 있다. 그러나 본 논문에서 제안한 TimesNet 모델은 이 작업에서 가장 우수한 성능을 발휘하며, 고급 MLP 기반 및 Transformer 기반 모델을 능가함을 보여준다.

- 4.3 IMPUTATION

Missing Value로 인해 Imputation 작업은 모델이 불규칙하고 부분적으로 관측된 시계열에서 잠재적인 시간적 패턴을 발견해야 하는 어려운 작업임에도, 표 4에서 볼 수 있듯이, TimesNet은 이해당 작업에서도 SOTA를 달성하여, 복잡한 시간적 변동을 포착하는 모델의 성능 또한 검증함.

- 4.4 CLASSIFICATION

시계열 분류의 경우 인식 및 의료 진단에 사용될 수 있으며, 이를 검증하기 위해, UEA 시계열 분류 아카이브 (Bagnall et al., 2018)에서, 의료 진단 및 기타 실제 작업을 포함하는 10개의 다변량 데이터셋을 전처리 하여 사용함.

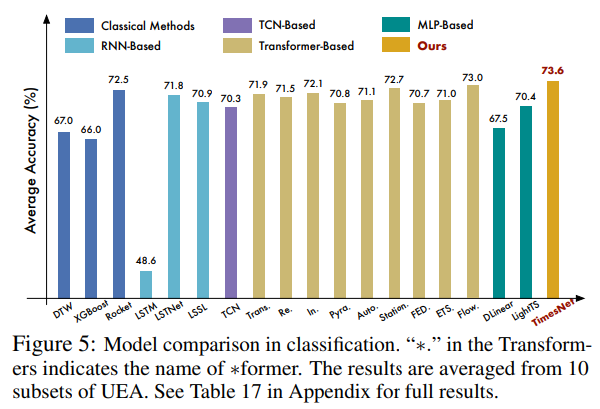
- 4.4 CLASSIFICATION

- 결과

Figure 5에서 볼 수 있듯이, TimesNet은 평균 정확도 73.6%로 최고의 성능을 달성하여 이전의 SOTA 방법인 Rocket (72.5%)과 딥 모델인 Flowformer (73.0%)를 능가함. 특히 MLP 기반 모델인 DLinear은 이 dataset 에서 잘 동작하지 않는데, (67.5%) 이는 DLinear의 경우 시간적 의존성이 고정된 자기회귀 작업에 적합한 한 계층의 MLP 모델만 사용하기 때문에, 고수준 표현을 학습하는 데 약점이 있을것으로 보임. 반면에 TimesNet은 2D 공간에서 시간적인 2D 변동을 통합하여 2D 커널을 통해 정보를 학습하기 용이하게 만들어지므로, 계층적 표현을 필요로 하는 분류 작업에 유리해 보임.

- 4.5 ANOMALY DETECTION

모니터링 데이터에서 이상치 탐지는 매우 중요하나, 일반적으로 데이터 레이블링이 어려워, unsupervised Leaning 방식으로 해당 Point 를 Detection 함. 비교 분석을 위한 벤치마크 데이터 셋은: SMD (Su et al., 2019), MSL (Hundman et al., 2018), SMAP (Hundman et al., 2018), SWaT (Mathur & Tippenhauer, 2016), PSM (Abdulaal et al., 2021).

- 결과

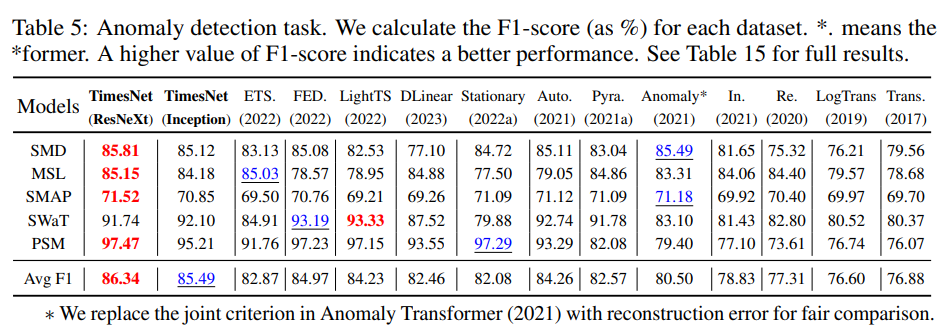Table 5를 보면, TimesNet이 이상 탐지에서 또한 SOTA를 달성하며, 고급 Transformer 기반 모델인 FEDformer (2022)와 Autoformer (2021)보다 뛰어남을 보여줌. 이는 이상 탐지가 드물게 나타나는 이상적인 시간 패턴을 찾아야 하는데 비해, 일반적인 어텐션 메커니즘은 각 시간 지점 쌍 간의 유사성을 계산하므로 주요 정상 시간 지점에 의해 방해를 받기 때문으로 보여짐. 또한TimesNet, FEDformer 및 Autoformer는 모두 휼륭한 성능을 공통적으로 보여 주는데 이러한 결과는 주기성 분석의 중요성을 보여주며, 주기성을 위반하는 변동을 암시적으로 강조하여 이상 탐지에 도움을 주는것으로 보임.

5.CONCLUSION AND FUTURE WORK

해당 논문의 novelty 는 다음과 같이 3가지로 요약된다.

-다양한 주기성과 주기별 내/외부적 상호작용에 대한 동기부여를 바탕으로, 우리는 시간적 변화 모델링을 위한 모듈화된 방법을 발견했습니다. 1차원 시계열을 2차원 공간으로 변환하여, 주기 내/외부적인 변화를 동시에 나타낼 수 있다.

-TimesNet은 TimesBlock을 사용하여 여러 주기를 찾고, parameter-efficient inception block으로 변환된 2D tensor에서 temporal 2D-variations을 포착하기 위한 새로운 task-general 모델로 제안된다.

-TimesNet은 단기 및 장기 예측, 대치, 분류 및 이상 탐지를 포함한 다섯 가지의 주요 시계열 분석 작업에서 일관된 최고 성능을 달성했다.