[ICLR 2023] Temporal 2D-Variation Modeling for General Time Series Analysis
Temporal 2D-Variation Modeling for General Time Series Analysis
1. Problem Definition
시계열 분석은 일기 예보, 이상치 탐지, 행동 인식 등 많은 응용 분야에서 사용되고 있습니다. 시계열 데이터는 언어나 영상과 같은 순차적 데이터와 달리 연속적으로 기록되며, 각 시점은 일부 값만 저장합니다. 하나의 단일 시점은 충분한 의미를 갖지 않기 때문에, 연속성, 주기성, 추세 등과 같은 시계열의 고유한 속성을 반영하도록 시간적 변화에 초점을 맞추고 있습니다.
2. Motivation
그러나 실제 시계열 데이터는 여러 변화(상승, 하락, 변동 등)가 복합적으로 섞여 복잡한 패턴을 포함하기 때문에 모델링이 어렵습니다.
이 논문은, 다중 주기성(multi periodicity)라는 관점에서 시계열 데이터를 분석하는 방법을 다룹니다. 날씨 관측을 예를 들면, 기온은 하루에도 주기성을 갖지만 주간, 월간, 분기간, 연간 주기성도 존재합니다.
두번째로, 각 주기 내에서 시계열 데이터는 인접한 영역 뿐만 아니라 인접한 주기의 변동과도 상관관계가 있다는 사실을 이용합니다. 저자들은 이를 각각 기간 내 변동(intraperiod-variation)과 기간 간 변동(interperiod-variation)이라 부릅니다.
기간 내 변동(intraperiod-variation): 기간 내의 짧은 주기성을 파악함.
기간 간 변동(interperiod-variation): 기간 간의 장기 추세를 파악함.

고전적인 방법론은 시간적 변동이 미리 정의된 패턴을 따른다고 가정합니다. 이런 방법론이 적용된 모델은 ARIMA, Holt-Winter, Prophet이 있습니다. 그러나 실제 시계열의 변화는 너무 복잡하여 이러한 사전 정의된 패턴으로 다루기 어렵기에 실제 적용은 매우 제한적입니다.
최근에는딥러닝을 이용한 방법론이 제안되었고, 크게 MLP, RNN, TCN 기반 모델이 있습니다.
- MLP-based: 시간차원을 고정된 layer로 인코딩
- TCN-based: 시간적 변화를 convolution-kernel을 이용하여 포착
- RNN-based: time step 당 상태 전환을 통해 시간적 변화를 포착
그러나 딥러닝 모델 역시 주기성에 의해 파생되는 시간적 변동을 고려하지 않습니다.
다양한 분야에서 좋은 성능을 보이는 Transformer 역시 시계열에서도 성능이 좋습니다. attention-mechanism을 이용하여 시점간의 시간적 의존성을 발견할 수 있습니다.
- Autoformer: auto-correlation을 이용하여 시간적 의존성을 포착하고
- FEDformer는 계절성-추세 분해를 이용하여 frequency 영역에서 attention을 포착합니다.
이 논문은 이전 연구와 비교하여 3가지 Contribution이 있습니다.
- Multi-periodicity를 포착하기 위해 1D time series를 2D tensor로 변환하여, intraperiod와 interperiod-variation 모두 포착
- TimesNet 모델 아키텍처 제안. 이때 parameter-efficient한 inception block이 적용된 TimesBlock 모듈 이용
- Foundation model로써, 5가지 주요 task에서 SOTA 달성 및 시각화 제공
3. Method
저자들이 제안한 TimesNet은 크게 2단계로 나누어 학습합니다. 첫번째 단계는 푸리에 변환을 이용하여 multi-periodicity를 포착하고, 두번째 단계는 앞서 얻은 period마다 2D-tensor로 변환하여 2D-variation을 포착합니다.
3.1 FFT Analysis
- $T$: 시계열 데이터의 길이
- $C$: 시계열 채널 수. univariate이면 $C = 1$이다
- $\mathbf{X}_ {\text{1D}} \in \mathbb{R}^{T \times C}$: 전체 시계열 데이터
- $\text{FFT}(\cdot)$는 고속 푸리에 변환으로 주파수 $f_i$를 찾는다
- $\text{Amp}(\cdot)$: 주파수 $f_i$의 진폭을 찾는 함수
- $\text{Avg}(\cdot)$: $C$차원 시계열 데이터에 대하여 진폭의 평균 계산
아래 일련의 과정을 거쳐 강도(indensity) $\mathbf{A}$를 얻습니다.
- $\mathbf{A} = \text{Avg}\Bigl( \text{Amp}(\text{FFT}(\mathbf{X}_ {\text{1D}})) \Bigr), \quad \mathbf{A} \in \mathbb{R}^T$

이때 $\mathbf{A}_ j$는 주파수가 $j$(주기가 $\lceil T/j \rceil$이다.)의 intensity가 된다. 주파수 영역에서 의미없는 고주파는 noise이므로 이를 제거하기 위해 top-$k$의 진폭만 사용하기로 합니다.
- ${ f_1, \cdots, f_k} = \underset{f_* \in {1, \cdots , [\frac{T}{2}]}}{\text{argTopK}(\mathbf{A})}, \quad p_i = \Biggl\lceil\cfrac{T}{f_i} \Biggr\rceil, \quad i \in { 1, \cdots, k }$
위 과정을 요약하면, $\mathbf{X}_ {\text{1D}}$로부터 FFT를 이용하여 $k$개의 유의미한 진폭($\mathbf{A}$), 주파수($f_i$), 주기($p_i$)를 얻습니다.
- $\mathbf{A}, {f_1, \cdots, f_k}, {p_1, \cdots, p_k} = \text{Period}(\mathbf{X}_ {\text{1D}})$
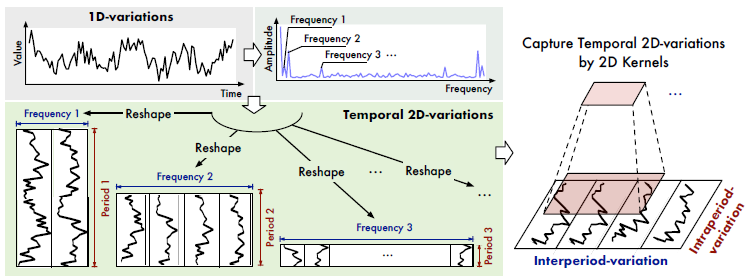
3.2 Reshape 1D time series to 2D tensors
FFT로 얻은 $f$와 $p$를 이용하여 $\mathbf{X}_ {\text{1D}}$로부터 $k$개의 2D-tensor $\mathbf{X}_ {\text{2D}}$ 를 얻을 수 있습니다. 이때 $\text{Reshape}$ 결과가 $p_i \times f_i$ 모양이 되도록 zero-padding $\text{Padding}(\cdot)$이 필요합니다.
$\mathbf{X}_ {\text{2D}}^i = \underset{p_i, f_i}{\text{Reshape}}(\text{Padding}(\mathbf{X}_ {\text{1D}})), \quad i \in { 1, \cdots, k }$
3.3 TimesBlock
TimesBlock 구조는 computer vision에서 자주 사용되는 ResNet의 residual way를 적용하였다. 먼저 raw data $\mathbf{X}_ {\text{1D}} \in \mathbf{R}^{T \times C}$를 모델 차원에 맞게 임베딩하여 $\mathbf{X}_ {\text{1D}}^0 \in \mathbb{R}^{T \times d_{\text{model}}}$를 얻게됩니다.
- $\mathbf{X}_ {\text{1D}}^0 = \text{Embed}(\mathbf{X}_ {\text{1D}}). \quad \mathbf{X}_ {\text{1D}} \in \mathbf{R}^{T \times C}, \ \mathbf{X}_ {\text{1D}}^0 \in \mathbb{R}^{T \times d_{\text{model}}}$
그 이후 $l$ 번째 layer마다 deep feature $\mathbf{X}_ {\text{1D}}^{l}$를 구한다.
- $\mathbf{X}_ {\text{1D}}^l = \text{TimesBlock}(\mathbf{X}_ {\text{1D}}^{l-1}) + \mathbf{X}_ {\text{1D}}^{l-1}$
TimesBlock은 크게 2가지 역할을 수행합니다.
- 2D-variation 포착
- Adaptively aggregating representations
Capturing temporal 2D-variations
TimesNet은 $\text{Reshape}(\cdot)$로 변환한 2D-tensor를 multi-scale 2D kernel로 학습합니다.
- $\mathbf{X}_ {\text{2D}}^i = \underset{p_i, f_i}{\text{Reshape}}(\text{Padding}(\mathbf{X}_ {\text{1D}})), \quad i \in {1, \cdots, k}$
이때 다양한 vision backbone을 이용할 수 있는데, 저자들은 parameter-efficient한 inception block을 사용했습니다.
- $\widehat{\mathbf{X}}_ {\text{2D}}^{l, i} = \text{Inception}(\mathbf{X}_ {\text{2D}}^{l, i}), \quad i \in {1, \cdots, k}$
$\text{Inception}(\cdot)$을 통해 표현된 $\widehat{\mathbf{X}}_ {\text{2D}}^{l, i}$은 다시 1D로 reshape하고 길이 $T$를 보존하도록 $\text{Trunc}(\cdot)$로 패딩을 제거합니다.
- $\widehat{\mathbf{X}}_ {\text{1D}}^{l, i} = \text{Trunc}(\underset{1, \ (p_i \times f_i)}{\text{Reshape}}(\widehat{\mathbf{X}}_ {\text{2D}}^{l, i})), \quad i \in {1, \cdots, k }$
각 $l$번째 layer를 통과한 후 $k$개의 1D-representation ${\widehat{\mathbf{X}}_ {\text{1D}}^{l, 1}, \cdots, \widehat{\mathbf{X}}_ {\text{1D}}^{l, k}}$을 얻습니다.
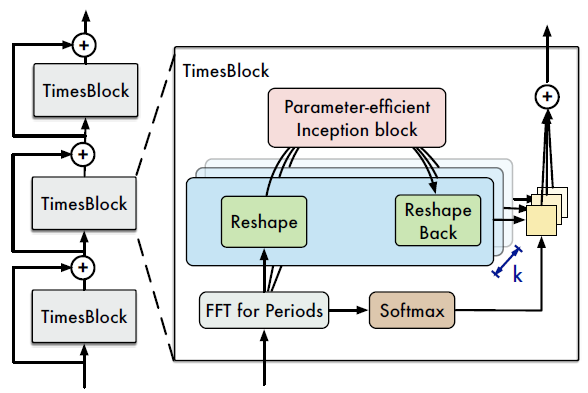
Adaptive aggregateion
Autoformer 모델이 제안된 논문에서, Auto-Correlation은 진폭 $\mathbf{A}$는 선택된 주파수와 주기 $f, p$의 상대적 중요성을 반영한다는 사실을 알아냈습니다. 따라서 진폭을 기반으로 1D-representation을 집계합니다.
- $\widehat{\mathbf{A}}_ {f_1}^{l-1}, \cdots, \widehat{\mathbf{A}}_ {f_k}^{l-1} = \text{Softmax}\left(\mathbf{A}_ {f_1}^{l-1}, \cdots, \mathbf{A}_ {f_k}^{l-1} \right)$
- $\mathbf{X}_ {\text{1D}}^l = \sum_{i=1}^{k} \widehat{\mathbf{A}}_ {f_i}^{l-1} \times \widehat{\mathbf{X}}_ {\text{1D}}^{l, i}$
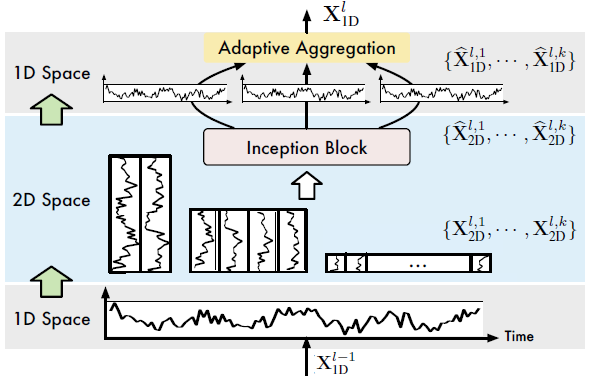
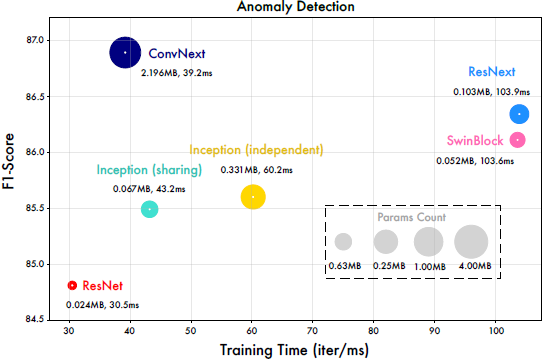
Generality in 2D vision backbones
저자들은 다양한 computer vision backbone인 ResNet, ResNeXt, ConvNeXt 등을 적용했습니다. 일반적으로 더 좋은 2D backbone일 수록 더 좋은 결과를 얻었습니다. 저자들은 성능과 효율성을 모두 고려하여 inception block을 선택했습니다.
4. Experiment
저자들은 시계열 분석에서 자주 사용되는 5가지 주제에 대하여 실험을 진행했습니다. 아래 표는 5개 task에 대하여 사용된 데이터셋, 평가지표 그리고 시계열 데이터 길이를 나타낸 것입니다.
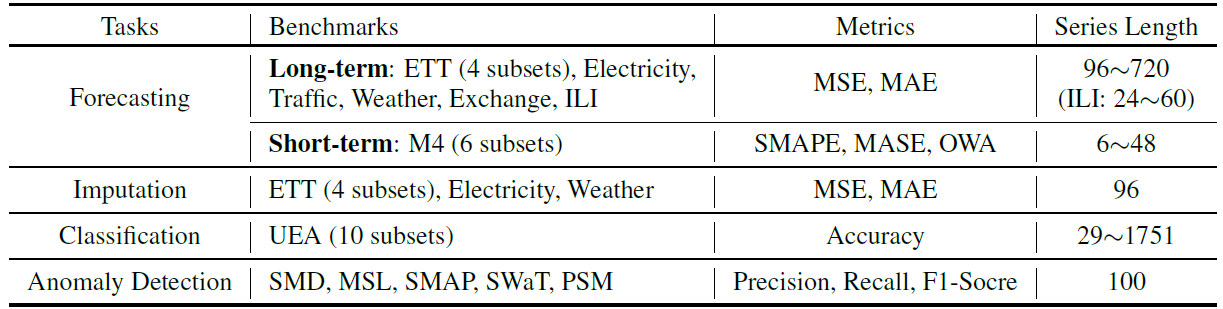
4.1 Main Results
TimesNet은 장기 예측, 단기 예측, 결측치 보강, 분류, 이상치 탐지 5개의 영역에서 모두 SOTA를 달성했습니다.
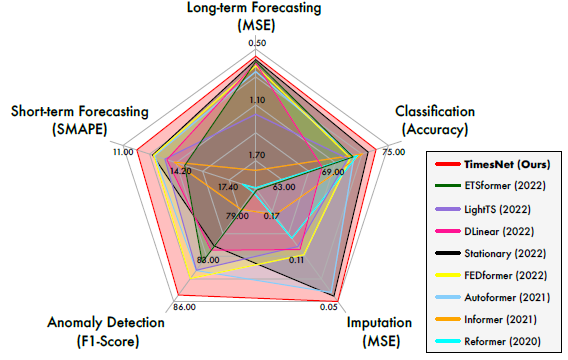
4.2 Short/Long-term Forecasting
TimesNet 장기 예측과 단기 예측 모두 좋은 성능을 보였습니다. 특히 장기 예측의 경우 80%의 데이터셋에서 SOTA를 달성했습니다. 특히 단기 예측에 사용된 M4 데이터셋의 경우 다양한 출처에서 데이터가 수집되어 시간적 변동이 큼에도 불구하고 다른 모델들 보다 성능이 좋습니다.
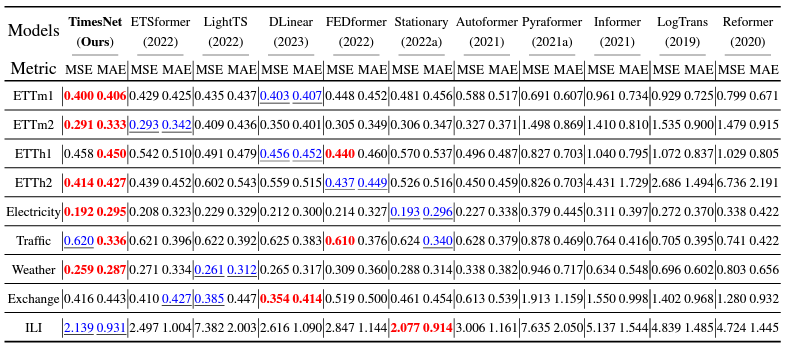

4.3 Imputation
결측치 때문에, 모델은 불규칙하고 불완전한 데이터 속에서 시간적 패턴을 찾아야 하기 때문에 어려운 문제입니다. 그럼에도 불구하고 TimesNet은 SOTA를 달성하여 극단적으로 복잡한 시계열 데이터에서 시간적 변동을 잘 포착한다는 것을 의미합니다.

4.4 Classification
시계열 데이터의 분류는 인지 및 의료 진단에 사용됩니다. 저자들은 UEA Time Series Classification Archive에서 행동, 동작 및 음성 인식, 심장 박동 모니터링을 통한 의료 진단 등의 실제 작업이 포함된 다변량 데이터셋 10개를 선택했습니다. 그리고 이런 데이터셋의 표준 데이터 전처리를 한 후 실험하였습니다.
 결과 역시 TimesNet은 SOTA를 달성하였습니다. 주목할 점은 장단기 예측에서 성능이 좋았던 MLP-based 모델들은 분류에서는 성능이 좋지 않다는 것입니다. 이는 TimesNet이 보다 더 높은 수준의 정보를 표현하기 때문에 계층 표현이 요구되는 분류 문제에서 성능이 좋다는 것을 의미합니다.
결과 역시 TimesNet은 SOTA를 달성하였습니다. 주목할 점은 장단기 예측에서 성능이 좋았던 MLP-based 모델들은 분류에서는 성능이 좋지 않다는 것입니다. 이는 TimesNet이 보다 더 높은 수준의 정보를 표현하기 때문에 계층 표현이 요구되는 분류 문제에서 성능이 좋다는 것을 의미합니다.
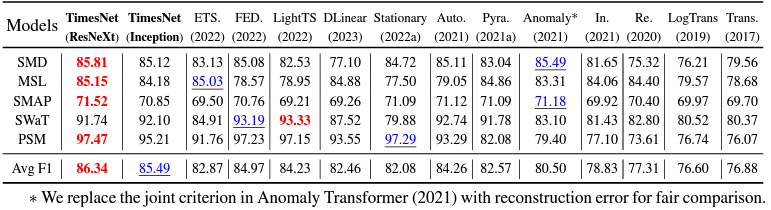
4.5 Anomaly Detection
이상치 탐지에서도 TimesNet은 SOTA를 달성했습니다. 이상치 탐지는 이상한 시간적 변동을 찾는 것이 요구되지만, Transformer는 attention-mechanism 특성상 정상 데이터가 영향을 많이 받기 때문에 성능이 그다지 높지 않았습니다.
4.6 Model Analysis
Representation analysis
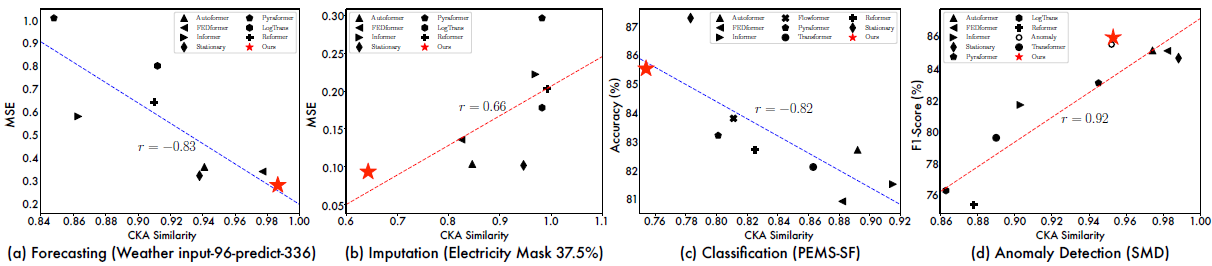
TimesNet은 예측과 이상치 탐지에서 CKA 유사도가 높고, 결측치 보강과 분류에서 CKA 유사도가 낮습니다. CKA 유사도가 낮다는 것은 각 layer끼리 구별된다는 뜻이고 곧 계층적 표현(hierarchical representation)을 의미합니다. 이는 TimesNet이 imputation과 classification에서 성능이 높은 이유를 설명할 수 있습니다.
반면에, FEDformer는 계층적 표현 학습에 실패하여 결측치 보강과 분류 작업에서 성능이 좋지 않음이 설명됩니다.
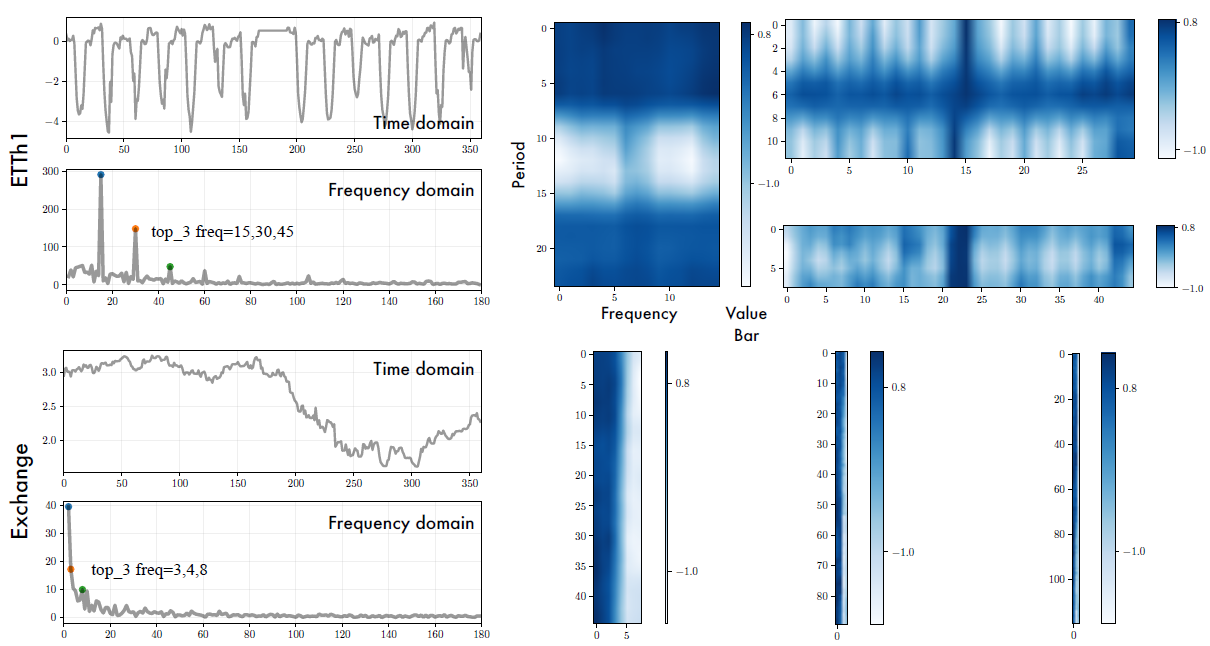
Temporal 2D-variations
- 기간 간 변동은 시계열의 장기 추세를 나타낼 수 있습니다.
- 명확한 주기가 없는 시계열의 경우에도 2D-tensor는 여전히 유용합니다. Exchange 데이터셋은 명확한 주기가 없지만 2D-tensor에서 장기 추세를 파악할 수 있습니다.
- 각 열(기간 내 변동)의 인접한 값은 가까운 시점의 지역성을 나타냅니다.
- 각 행(기간 간 변동)의 인접한 값은 기간 끼리의 지역성을 나타냅니다.
- 이러한 지역성은 표현 학습에 2D-kernel을 이용하는 동기가 됩니다.
2D-tensor를 시각화면 아래 그림과 같습니다.
5. Conclusion
- TimesNet은 시계열 분석 영역에서 task-general foundation model입니다.
- 다중 주기성을 이용하여 TimesNet은 주기내 변화와 주기간 변화 모두 포착합니다. (다양한 시간적 변화 포착)
- 다양한 데이터셋 실험에서 TiemsNet은 5가지 task에 SOTA를 달성했습니다.