[ICDM 2023] Reserve Price optimization in First-Price Auctions via Multi-Task Learning
Glossary
Publisher : Advertiser가 맏긴 광고를 게재해주는 업체,출판사 (e.g., Forbes)
Advertiser : Publisher에게 광고게재를 맡기는 기업,회사 (e.g., Volkswagen)
Reserve price : Publisher가 광고게재를 받아들일 최소 가격
AD impression : 온라인 페이지에서의 광고 표시(One display of an AD in a page view)
RTB : Real-time-bidding
1. Problem Definition
온라인 디스플레이 광고는 advertiser로부터 받은 돈을 대가로 advertiser에 대한 정보와 서비스를 제공하는 대부분의 publisher의 가장 중요한 수익원이다. 현재는 광고게재를 위해 실시간으로 advertiser가 입찰하는 RTB방식으로 광고가 판매된다. Reserve price보다 높은 가격으로 입찰한 advertiser중, 가장 높은 금액을 제시한 advertiser는 최종적으로 publisher의 웹페이지에 본인들의 광고를 게재할 수 있게된다. 기존에는 winning advertiser가 두번째로 높았던 입찰가를 지불하는 second-price auction방식이 주로 사용되어왔으나, 2019년부터는 winning advertiser가 제안한 가장 높은 입찰가를 지불하는 first-price auction방식이 사용되고 있다.
first-price auction에서는 advertiser측에서 publisher가 사전에 정해놓은 reserve price보다 훨씬 높은 금액을 제시하여 winning advertiser가 되었다면, 본인들이 제시한 금액을 전부 지불하여 광고를 게재하는 방식이다. 또한 first-price auction에서는 모든 입찰가가 reserve price보다 낮다면 모든 광고를 게재하지 않는다. 따라서 publisher는 reserve price보다 큰 입찰가중에서 highest bid (가장 높은 금액)이 본인들의 수익이 되므로 최적의 reserve price를 설정하는것이 매우 중요하다. reserve price에 따라 분류될 수 있는 입찰의 종류는 다음과 같다.

- Underbid Impressions : Reserve price > the higest bid
- 여러 advertiser가 제시한 모든 금액이 publisher가 설정한 reserve price보다 낮으므로 publisher는 어떤 광고도 게재하지 않으며, 수익을 창출하지 못함
- publisher는 수익 창출을 위해 다음 입찰의 reserve price를 advertiser가 제시한 highest bid보다 조금낮게 하향조정할 필요가 있음
- 그러나 Underbid가 발생하면 publisher측은 이전 입찰에서 advertiser가 reserve price보다 낮은 금액을 제시한 사실만 알 수 있고, 정확한 제시 금액을 알 수 없음
- Outbid Impressions : Reserve price <= the higest bid
- 이 경우 가장 높게 제시된 금액이 publisher의 수익이 됨
- reserve price가 너무 낮게 설정되면, advertiser는 높은 금액을 제시하지 않아 수익을 극대화하기 어려움
- Outbid 상황에서 일반적으로, 높은 확률로 advertiser는 reserve price보다 조금 높은 금액을 제시하는 경향이 있음
- 따라서 publisher는 highest bid보다 조금 낮은 금액을 reserve price로 설정한다면 advertiser들의 경쟁을 부추겨 수익을 극대화할 수 있음
이처럼 first-price auction에서 최적의 reserve price를 설정하는것은 고려해야할 요소가 매우 많은 복잡한 문제이며 publisher의 수익에 직접적인 영향을 미치는 요소이다.
2. Motivation
first-price auction에서 reserve price를 예측하는 것을 어렵게 만드는 대표적인 이유들은 다음과 같다.
- advertiser들의 highest bid를 직접 예측하는것은 매우 risky함
- 과거 outbid의 거래 데이터를 바탕으로 advertiser의 highest bid를 바로 예측하는 ML모델을 구축하여 reserve price설정에 활용할 수 있음
- 그러나 광고시장 자체의 불확실성, data noise, 구축한 ML 모델의 오작동과 같은 이유들이 publisher의 수익창출에 불확실성을 제공함
- Underbid가 발생하면 publisher가 reserve price를 예측하는데 highest bid를 직접적으로 사용할 수 없음
- Underbid에서 publisher는 설정한 reserve price를 바탕으로 underbid가 발생한 사실만 알 수 있음
- advertiser가 제시한 정확한 highest bid를 알 수 없으므로, underbid의 highest bid를 직접적으로 사용하지못함
- publisher는 user에 대해 매우 제한적인 정보만을 가짐
- user와 platform을 통해 직접적으로 소통하는 advertiser대비 publisher는 user에 대한 정보를 많이 알기 힘듦
3가지 어려움을 다루기 위해 해당 논문에서 제시한 solution은 다음과 같다.
Solution to 1
- highest bid $b$를 점추정을 통해 직접 구하지 않고 구간추정을 사용해 $[b_ {L},+\infty]$을 구함
- publisher의 전략을 반영할 수 있는 confidence level (1 − $\alpha$)에 따라 highest bid의 하한인 $b_L$을 예측함
- 예를들어, publisher가 high risk-high return 전략을 택한다면 $\alpha$(risk level)를 늘리고, low risk-low return 전략을 택하면 $\alpha$를 줄여 $b_ {L}$을 계산
Solution to 2
- main task가 highest bid의 하한인 $b_ {L}$을 예측하고 auxiliary task가 설정된 reserve price가 underbid될 확률을 계산하는 multi-task learning을 도입함
- outbid 데이터만 활용해 highest bid $b$만 추정하는 선행 연구와 달리, underbid 데이터 또한 사용하여 outbid,underbid 데이터를 모두 활용함
- multi-task learning을 통해 공유된 learning parameters를 바탕으로 main task의 성능또한 향상시킬 수 있음
Solution to 3
- DNN을 사용하여 feature간 복잡한 관계를 파악
- publisher가 가진 data를 바탕으로 user, page등 각 feature에 embedding을 적용하여 latent feature를 학습 및 활용
3. Method
- Main task를 통해, advertiser의 highest bid가 최소 (1 − $\alpha$)%확률로 outbid될 수 있도록 하는 reserve price의 하한 $b_ {L}$를 예측함

- 예측된 $b_ {L}$을 바탕으로 underbid될 확률(failure rate) $h$를 예측할 수 있으므로 main task와 auxiliary task는 밀접하게 관련이 있음
3.1-A Loss of Highest Bid Lower Bound Prediction
main task의 loss function을 정의하게 위해 해당 논문에서는 [1]에서 제시한 QD loss function을 활용한다. QD는 데이터의 특정 비율을 캡쳐하여 가능한 좁은 고품질의 예측 구간을 생성하는 방식으로, 전통적인 방법에 비해 직접적으로 예측 구간의 품질을 향상시킬 수 있다. QD loss function의 overall loss는 두가지 요소의 합으로 구성된다.
1. Captured Mean Prediction Interval Width($MPIW_ {capt}$)
$MPIW_ {capt-(1)} = \frac{1}{\sum_{i=1}^{n} k_i}(\hat{b}_ {U_ {i}}-\hat{b}_ {L_ {i}})k_ {i}$
- 가능한 좋은 예측 구간을 파악하기위해, ground truth를 포함하는 예측구간의 평균 너비를 측정
- $k_ {i}$는 $i$번째 sample의 ground truth가 추정된 예측구간에 포함된 여부를 나타내는 Boolean
- $MPIW_ {capt-(1)}$값이 높을수록 추정된 예측구간의 퀄리티가 좋음
- 그러나 highest bid의 upper bound($\hat{b}_ {U_ {i}}$)는 $+\infty$이므로 $MPIW_ {capt-(1)}$수식을 적절히 수정할 필요가 있음
$MPIW_ {capt-(2)} = -\frac{\hat{b}_ {L_ {i}}k_ {i}}{\sum_{i=1}^{n} k_i}$
- 다음처럼 수정하여 highest bid의 하한($\hat{b}_ {L_ {i}}$)만 고려할 수 있음
2. Prediction Interval Coverage Probability(PICP)
$PICP = \frac{1}{n}\sum_{i=1}^{n} k_i$
- 전체 중 몇개의 ground truth가 정확하게 예측구간에서 capture되었는지를 나타내는 예측구간의 coverage 확률
- $PICP$는 예측구간의 quality를 나타내는 매우 중요한 척도임
3. QD Loss function
- 모델에서는 $L_ {\theta} = L( \theta \vert k, \alpha)$ 에 대한 negative log likelihood 를 최소화 하는 $\theta$ 를 학습함 ($\alpha$ 는 risk level)
- $L_ {\theta} = \frac{n!}{c!(n-c)!}(1-\alpha)^ c\alpha^ {n-c}(c = \sum_{i=1}^{n} k_i)$
- 위의 이항분포 식은 Moivre-Laplace theorem에 의해 정규분포로 근사될 수 있고 negative log likelihood는 다음과 같음
$-logL_ {\theta} \propto \frac{n}{\alpha(1-\alpha)}((1-\alpha)-PICP)^ {2}$
- 위의 변형들을 통해 예측구간의 coverage 확률과 너비를 동시에 고려한 highest bid의 하한을 예측을 진행할 수 있으며 최종 QD loss function은 다음과 같음
$Loss_ {qd} = MPIW_ {capt} + \lambda PICP = -\frac{\hat{b}_ {L_ {i}}k_ {i}}{\sum_{i=1}^{n} k_i} + \lambda \frac{n}{\alpha(1-\alpha)} max(0, (1-\alpha)-\frac{1}{n} \sum_ {i=1}^{n} k_i)^2$
($\lambda 는 PICP$의 중요도를 조절하는 parameter)
3.1-B Loss of Failure Rate Prediction
Underbid가 발생하면 advertiser가 제시한 highest bid를 알 수 없으므로 3.1-A에서 제시한 QD estimation을 적용할 수 없다. 따라서 하나의 impression을 일련의 feature를 가진 instance로 정의하고 survival analysis을 적용하여 outbid impression과 underbid impression를 모두 활용한 reserve price의 failure rate(underbid될 확률)을 계산한다. 본 논문에서는 [2]에서 제시한 the Cox PH model을 활용한다.
$h(t,X_ {i}) = h_ {0}(t)e^ {\hat{y}_ {i}}$
the Cox PH model은 두가지 부분으로 구성되어있고 설명은 다음과 같다.
$h_ {0}(t)$ : underlying baseline harzard function, describes how the risk of an event per time unit changes over t at baseline levels of explanatory variable
$\hat{y}_ {i}$ : describes how the hazard varies in response to explanatory variables $X_i$
또한 the Cox PH model에서는 baseline harzard function $h_ {0}(t)$의 분포에대한 가정이 필요하지 않은데, 이런 특징이 복잡하고 동적인 광고 시장에서의 문제에 적용하기 용이하게 만든다. 따라서 the Cox PH model을 통해 특정 reserve price $r_i$에서 impression $X_i$가 underbid될 확률 $h(r_ {i},X_ {i})$을 계산할 수 있다.
the COX partial liklihood function을 사용해 $\theta$를 추정한다면 outbid impression과 underbid impression를 모두 활용할 수 있다. reserve price가 $r_ {i}$일때 하나의 underbid impression($A_ {i}$)에 대해 $b_ {j}(highest bid)>r_ {i}$를 만족하는 모든 outbid impression($A_ {j}$)을 사용하여 $h(r_ {i}, X_ {i}) - h(r_ {i}, X_ {j})$를 최대화 하는 $\theta$를 찾고자 한다. reserve price = $r_ {i}$의 partial likelihood를 통해 outbid impression과 비교하여 underbid impression의 상대적인 가치를 학습할 수 있으며 수식은 다음과 같다.
$L_ {i} = \frac{h(r_ {i},X_ {i})}{\sum_{j:b_ {j} \geq r_ {i}}^{} h(r_ {i},X_ {i})}=\frac{h_ {0}(r_ {i})e^{\hat{y}_ {i}}}{\sum_{j:b_ {j} \geq r_ {i}}^{} {h_ {0}(r_ {i})e^{\hat{y}_ {i}}}} = \frac{e^{\hat{y}_ {i}}}{\sum_{j:b_ {j} \geq r_ {i}}^{} e^{\hat{y}_ {i}}}$
각 impression이 독립일때 underbid impression의 joint probability은 $L_ {\theta} = \Pi_ {A_ {i}\in U}L_ {i}$($U$는 underbid impression의 집합)이다.
Cox모델의 loss(negative log partial likelihood)는 다음과 같다
$Loss_ {cox} = {\sum_{A_ {i} \in U} (log \sum_{j:b_ {j} \geq r_ {i}}e^{\hat{y}_ {i}}-\hat{y}_ {i}})$
따라서, multi-task learning의 최종 loss function은 다음처럼 정의된다.($\mu$는 failure rate의 중요성을 조절하는 parameter)
$Loss = Loss_ {qd} + \mu Loss_ {cox} = -\frac{\hat{b}_ {L_ {i}}k_ {i}}{\sum_ {i=1}^{n} k_ i} + \lambda \frac{n}{\alpha(1-\alpha)} max(0, (1-\alpha)-\frac{1}{n}\sum_ {i=1}^{n} k_ i)^2+\mu{\sum_ {A_ {i} \in U} (log \sum_ {j:b_ {j} \geq r_ {i}} e^{\hat{y}_ {i}}-\hat{y}_ {i}})$
3.1-C Predicting Highest Bid Lower Bounds and Failure Rates
ad impression의 가치가 다음 4가지 feature에 영향을 받음에 착안하여 multi-task learning의 loss function을 최소화하는 $\hat{b}_ {L_ {i}}$, $\hat{y}_ {i}$를 찾는 모델을 구축한다.
1. User interest
- Main idea : 사용자가 product에 관심이 많으면, advertiser 또한 많은 투자를 할것임
- user ID, state-level locations, operating systems, Internet browser types,network bandwidths, devices와 같은 publisher선에서 접근가능한 사용자의 feature들을 모델에서 사용
2. AD placement
- Main idea : [3]에따라, 광고가 페이지의 상단에 존재할때 더 가시성이 좋으며 높은 bid를 유도함
- ad position, ad unit size 두가지 placement feature들을 모델에서 사용
3. Page information
- Main idea : 예를들어, 정치 기사가 실린 페이지를 읽는 user보다 전자제품 기사가 실린 페이지를 읽는 user가 쇼핑 의도가 있을 가능성이 더 높음
- page URLs, channels(e.g., business, lifestyle), sub-channels/sections, the trending status of the page labeled by the publishers’ editors와 같은 feature 사용
4. Context
- Main idea : 광고의 가치는 광고를 보는 상황에서의 context에 영향을 받음
- include hour of the day, referrer URLs(i.e., in which page the request for the current page originated) feautre 사용
RTB 알고리즘과 광고시장의 불확실성 등을 고려했을때 latent feature와 feature간 상호작용을 파악하는것이 중요하므로 DNN architecture을 사용한다. parameter를 공유하는 multi-task learning을 적용하기위한 learning framework는 아래와 같다.
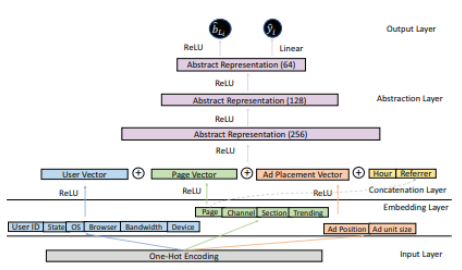
각 layer에 대한 설명은 다음과 같다.
Input layer : 모든 input feature들은 범주형이거나 쉽게 범주형으로 변환될 수 있으므로, one-hot encoding을 적용한다.
Embedding layer & Concatenation layer : User, page, ad placement feature들을 각 latent embedding vector로 표현하여 모델 성능 향상을 도모한다. 앞에 언급한 3개의 feature들이 ReLU함수에 매핑되어 embedding vector로 표현되고, 각 embedding vector들과 context feature를 concat한 unified vector를 생성한다. 이 과정을 통해 데이터간 비선형 관계와 상호작용을 효과적으로 학습할 수 있다. (widths of embedding = 128)
Abstraction layer : Concatenation layer에서 생성된 unified vector가 3겹의 abstraction layer를 거쳐 더 dense한 표현으로 변환되도록 하여 모델의 성능을 향상시킬 수 있도록 한다. (widths of abstraction = 256,128,64)
Output layer : [0,+$\infty$]의 범위를 가지는 highest bid의 하한 $\hat{b}_ {L_ {i}}$, the Cox PH model의 exponential인 $\hat{y}_ {U_ {i}}$를 예측하여 최종 loss function을 계산한다.
4. Experiment
4.1-A Experiment setup
- Dataset : first-price auctions collected on the Forbes Media’s website in early 2021
- Computer Spec : Desktop with an i7 3.60Hz CPU, 32GB RAM, and an NVIDIA GeForce GTX 1060 6G GPU
- Using Stochastic Gradient Descent (SGD) optimizer with a learning rate of $10^ {-3}$
-
traning batch size is 256
-
$\alpha$(risk level) = 30%, $\lambda$(PICP의 중요도를 조절하는 parameter) = 10, $\mu$(failure rate의 중요도를 조절하는 parameter) = 0.1
- Evaluation Metrics
- $PICP$(Prediction Interval Coverage Probability)
- 몇개의 ground truth가 정확하게 예측구간에서 capture되었는지를 나타내는 예측구간의 coverage 확률
- $PICP$는 (1-$\alpha$)% 이상이길 예상됨
- $MORP$(Median Outbid Reserve Price)
- 모든 testing outbid impressions에 대한 예측 reserve price의 median
- $MORP$는 predicted reserve price가 얼마나 높은지를 반영함
- section 3에서 제시한 $MPIW$는 음수 값을 가지고 덜 직관적이므로, $MORP$를 사용
- $CORP$(Covered Outbid Reserve Price)
- $CORP$ ~ $PICP$ * $MORP$
- $PICP$와 $MORP$를 balancing한 unifed metric
- balancing을 통해 predicted reserve price와 higehst bid의 관계를 반영한 예측 reserve price의 average
- $CORP$를 통해 모델이 얼마나 정확하게 reserve price를 예측하는지 판단가능
- $PICP$(Prediction Interval Coverage Probability)
4.1-B Comparison System
일반적으로 예측구간 추정에 많이 사용되는 3가지 방법과 해당 논문의 방법론의 성능을 비교한다. 비교대상이 될 방법론은 다음과 같다.
1.MVE(Minimum Variance Estimation)
- Error가 target의 실제 평균을 중심으로 정규분포를 따르며, input의 집합에 대해 target의 분산이 dependence하다고 가정
- NN을 사용해 $\hat{\mu}$, $\hat{\sigma^ {2}}$를 예측하며, 최종 reserve price 하한 $\hat{b}_ {L_ {i}}$에 대한 $\alpha$(risk level)를 구함
$\Phi(\hat{b}_ {L_ {i}})=\alpha$
2.Bootstrap
- 다른 parameter의 subset을 사용해 $B$개의 NN을 만든후, ensemble을 통해 collective한 decision을 내림
$\hat{y} = \sum_ {h=1}^{B} \hat{y}_ {h}$
$\hat{\sigma}_ {\hat{y}}^{2}=\frac{1}{B-1}{\sum_ {h=1}^{B} (\hat{y}_ {h}-\hat{y})}$
$\hat{y} \pm t_ {1-\frac{\alpha}{2},df} \sqrt{ \hat{\sigma}_ {\hat{y}}^{2}+ \hat{\sigma}_ {\epsilon}^{2}}$
- 위의 예측구간을 통해 $\alpha$(risk level)를 반영한 $\hat{b}_ {L_ {i}}$를 구함
3.LUBE
-
$PICP$ 와 normalized $MPIW$를 고려한 method
-
예측 구간의 폭을 줄이면서 $PICP$를 늘릴 수 있는 $\hat{b}_ {L_ {i}}$를 구함
4.1-C Performance by method
QD : reserve price의 하한이 highest bid를 포함할지만을 예측
QD + Cox : QD에 더불어 reserve price의 하한이 highest bid를 초과할 가능성 또한 고려함
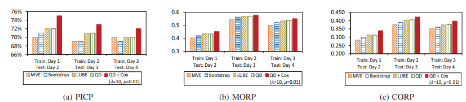
모든 metric에 대해 해당 논문에서 제시한 QD + Cox 가 가장 성능이 좋음을 알 수 있다.
예측구간이 ground truth를 포함할 확률인 $PICP$측면에서 다른 방법론들은 risk를 고려한 최소 커버확률인 70% (1-$\alpha$)를 달성하지 못하는 경우도 있으나, QD + Cox모델은 항상 70%를 만족함과 동시에 가장 높은 $PICP$를 달성하였다.
$MORP$측면에서도 QD + Cox모델의 성능이 가장 우수함을 알 수 있다. 일반적으로, $MORP$가 높으면 reserve price가 높으므로 highest bid를 포함하지 못할 확률이 낮아질 수 있어 $PICP$가 낮다. 그러나 MVE와 bootstrap에서는 타 방법론보다 상대적으로 $MORP$가 낮음에도 불구하고 $PICP$가 낮은데, 이는 두 방법론이 RTB 광고 시장에서 사용하기 다소 적합하지 않음을 시사한다. 또한 $PICP$와 $MORP$를 동시에 사용하는 $CORP$에서도 QD + Cox모델의 성능이 가장 우수하다. 이를 통해 해당 논문에서 제시한 모델에서 예측한 reserve price의 하한이 가장 높은 확률로 advertiser의 highest bid를 포함할 수 있으며, reserve price의 하한이 가장 큰 값을 예측함으로써 publisher가 효과적으로 수익을 최대화 할 수 있게된다.
4.1-D Performance with Different Risk levels
가장 좋은 성능을 보였던 hyperparmeter의 조합인 $\lambda$ = 10, $\mu$ = 0.1을 대상으로 $\alpha$(risk level)을 바꿔가며 QD + Cox모델의 performance를 확인하였다.

$\alpha$가 높아짐에 따라 $PICP$는 점점 낮아지지만 $MORP$는 높아지는 결과를 확인하여 high-risk전략을 취하면 수익을 전혀 얻지 못할 확률이 높아지나, 수익이 발생하면 많은 금액을 publisher가 벌 수 있음을 알 수 있다. 반대로 low-risk전략을 취하면 수익을 전혀 얻지 못할 확률은 낮으나, publisher는 비교적 적은 금액을 벌게된다.
(a)의 결과를 통해 $\alpha$=10%,20%로 상대적으로 낮을때 높은 수준의 coverage를 기대하나, $PICP$가 (1-$\alpha$)%이상 만족되지 않음을 알 수 있다. 이 결과는 광고시장이 가지는 불확실성, data noise때문이며 마냥 낮은 수준의 $\alpha$가 무조건적인 coverage를 보장하지 않는다는 것을 알 수 있다.따라서 publisher는 해당 문제를 인식하고 적합한 수준의 $\alpha$를 설정할 필요가 있다.
또한 $MORP$는 $\alpha$=40%일때가 가장 높지만, $PICP$까지 함께 고려한 reserve price인 $CORP$는 $\alpha$=30%일때 가장 높음을 알 수 있다. 이는 $\alpha$=40%일때, risk가 증가함에따라 coverage될 확률이 급격히 낮아져 $PICP$가 $CORP$에 큰 영향을 미쳤기 때문이다.
따라서 높은 $\alpha$에서는 underbid를 발생시킬 확률이 높으나, outbid가 발생만 하게된다면 publisher가 높은 수익을 얻을 수 있다. 반대로 낮은 $\alpha$에서 publisher가 많은 impression을 판매할 수는 있지만, advertiser의 RTB 알고리즘이 높은 bid를 제시할 필요가 없음을 빠르게 알 수 있어 지속적으로 높은 bid를 제시하지 않아 publisher가 수익을 최대화 하긴 어렵다. 따라서 적절한 risk level을 설정하는것 또한 publisher의 수익에 지대한 영향을 미침을 알 수 있다.
5. Conclusion
First-price auction에서 publisher가 ad 판매로 수익을 최대화하고 advertiser로 하여금 미래에 더 높은 가격으로 bid하게 유도하는데에 최적의 reserve price를 설정하는것이 매우 중요한 task이다. 해당 논문에서는 publisher가 설정한 risk level($\alpha$)에 따라 예측되는 advertiser의 highest bid와 underbid될 확률을 multi-task framework를 사용하여 효율적으로 예측하는 DNN 모델을 제시하였다. DNN에서 publisher의 광고판매를 통한 수익에 영향을 줄 수 있는 feature들을 고려하였으며, 해당 QD + Cox 모델이 타 방법론 대비 우수한 성능을 제시함과 동시에 publisher에게 다양한 insight를 제시하였다.
6. Reference & Additional materials
[1] T. Pearce, A. Brintrup, M. Zaki, and A. Neely, “High-quality prediction intervals for deep learning: A distribution-free, ensembled approach,” in ICML’18. PMLR, 2018, pp. 4075–4084.
[2] D. G. Kleinbaum and M. Klein, Survival Analysis. Springer, 2010.
[3] C. Wang, A. Kalra, L. Zhou, C. Borcea, and Y. Chen, “Probabilistic models for ad viewability prediction on the web,” TKDE, vol. 29, no. 9, pp. 2012–2025, 2017.
Author Information
- Jeongmin Son
- Contact : jmson@kaist.ac.kr
- Affiliation : CSD Lab(https://csdlab.kaist.ac.kr/)