description : Wang, Hongwei et al. / Relational Message Passing for Knowledge Graph Completion / KDD-2021

Relational Message Passing for Knowledge Graph Completion

1. Problem Definition

지식 그래프는 Entity와 Relation으로 지식 구조를 그래프로 표현한 것입니다.
Entity는 그래프의 node와 같은 역할이며, 지식 그래프의 개체를 나타냅니다.
Relation은 그래프의 edge와 유사하며, 지식 그래프에서 연결된 개체간의 관계를 나타냅니다.
예를 들어, Entity pair ‘Mona Lisa”와 ‘Da Vinci’ 사이에는 ‘painted by’의 relation이 존재합니다.
일반적으로 지식 그래프는 규모가 크며 불완전하므로 missing relation을 예측해 완전하게 만드는 것이 목표입니다.

entity pair $(h,t)$가 주어졌을 때 entity간의 relation인 $r$의 분포를 모델링합니다. 베이즈 정리에 의해 다음과 같이 나타낼 수 있습니다. $p(r|h,t) \propto p(h,t|r) \cdot p(r)$

$p(r)$은 prior distribution이므로, $p(h,t|r)$을 모델링합니다. $p(h,t \vert r)=\frac{1}{2}(p(h \vert r) \cdot p(t \vert h,r)+p(t \vert r) \cdot p(h \vert t,r))$

여기서 $p(h|r), p(t|r)$은 주어진 relation에 대한 entity의 likelihood입니다.
본 논문의 모델에서는 entity의 자체 특징을 이용하지 않으므로, entity의 local relational subgraph로 대체합니다.
이로부터 entity에 인접한 relation set에 대해 생각할 수 있습니다.

$p(t|h,r)$, $p(h|t,r)$는 entity와 relation이 주어졌을때 다른 entity에 어떻게 도착할지에 대한 likelihood입니다.
이는 entity와 entity 사이의 경로를 모델링하는 문제가 됩니다.

2.Motivation

기존 방법은 relation type 정보를 효과적으로 파악하지 못했고, 이를 해결한 방법은 복잡도가 높다는 단점이 있다. 대부분의 기존 연구에서는 entity와 relation을 embedding space에 나타내고 이를 학습하는 방법을 제안했습니다.
그러나 학습하지 않은 데이터에 대해 예측하는 inductive setting에서 한계를 보이므로, 이를 해결하기 위해 GNN의 아이디어를 가져오게 됩니다.
일반적으로 지식 그래프에서 relation type은 균일하게 나타나지 않고, 공간적으로 연관되어 있다는 특징이 있습니다.

예를 들어 지식 그래프에 ‘보유하다’, ‘구매하다’, ‘헤엄치다’, ‘졸업하다’의 relation이 있다고 합시다.
‘보유하다’와 가장 가까운 relation으로 ‘구매하다’가 ‘헤엄치다’, ‘졸업하다’보다 더 적합할 것입니다.

따라서 relation type을 특성화한다면 추론하는데 있어서 중요한 정보를 제공하게 됩니다.
이러한 정보를 효과적으로 얻기 위해 인접한 개체의 정보를 통합해 전달하는 message passing 이 적용되었습니다.

기존에는 node간의 message passing을 통해 정보를 얻었으나, 이 문제에서는 인접한 relation의 관계를 통해서 해결하고자 하므로 edge에 message passing을 적용하는게 더 적절합니다.
이 방법을 Relational Message Passing이라고 하며, 다음의 장점이 있습니다.

inductive setting에서도 효과적으로 예측할 수 있다.
entity의 embedding을 계산하지 않으므로 효율적이다.
relation type간의 correlation을 통해 예측 결과를 설명할 수 있다.

그러나 각 entity에서 인접한 모든 relation의 정보를 결합해서 전달하므로 relation이 많을수록 계산 복잡도가 크게 증가한다는 단점이 있습니다.

본 논문은 인접한 relation의 정보를 결합하는 과정을 2단계로 나눠 계산 복잡도를 낮추고, relation의 2가지 structure를 활용해 missing relation을 예측하는 모델을 제안합니다.

3. Method

Methodologies

Message Passing

Node-based message passing 초기 message passing은 node를 기반으로 했으며 다음의 과정을 반복해서 학습합니다. $m_{v}^{i}=A(\lbrace s_{u}^{i}\rbrace_{u \in N(v)}),$ $s_{v}^{i+1}=U(s_{v}^{i}, m_{v}^{i})$ $s_{v}^{i}$: node v의 i번째 iteration에서의 hidden state
$m_{v}^{i}$: node v가 i번째 iteration에서 받은 message
$N(v)$: node v에 인접한 모든 node

인접한 모든 node의 정보를 aggregate하고 자신의 정보와 함께 input으로 넣어 update합니다.

지식 그래프에서는 edge는 feature(relation type)를 가지나 node는 그렇지 않습니다.
또한 node의 수가 edge보다 훨씬 많으므로, iteration마다 node embedding 정보를 저장해야 함에 따라 메모리 문제가 발생합니다.
Relational message passing
위의 문제를 해결하기 위해 edge에 message passing을 적용한 방법이 제안되었습니다.
이를 message passing이라고 하며, 학습 과정은 다음과 같습니다. $m_{e}^{i}=A(\lbrace s_{e'}^{i}\rbrace_ {e' \in N(e)}),$ $s_{e}^{i+1}=U(s_{e}^{i},m_{e}^{i})$

edge $e$와 인접한 edge의 정보를 aggregate하고 자신의 정보와 함께 input으로 넣어 update합니다.
$N$ nodes, $M$ edges, node degree의 분산 $var[d]$에 대해 회당 기대 계산 비용은 다음과 같습니다.
node-based message passing: $2M+2N$
relational message passing: $N \cdot Var[d]+\frac{4M^2}{N}$

relational message passing은 이전의 문제들을 해결할 수 있었으나, edge의 개수가 많아지면 복잡도가 크게 증가한다는 문제점이 있습니다.
이에 본 논문의 저자들은 새로운 방법을 제안합니다.

PATHCON

Notations

여기부터는 논문에서 제안하는 모델에 대한 설명입니다. Notation이 다음과 같이 정리됩니다.
$h, t$: head entity, tail entity
$r$: relation type
$s_{e}^{i}$: i번째 iteration에서 edge e의 hidden state
$m_{v}^{i}$: i번째 iteration에서 node v의 message
$N(e)$: edge e의 endpoint nodes
$N(v)$: node v의 인접한 edges
$s_{(h, t)}$: entity 쌍 $(h,t)$의 context representation
$s_{h \rightarrow t}$:entity h에서 t로 가는 모든 path의 representation
$\alpha_P$: path P의 attention weight
$P_{h \rightarrow t}$: entity h에서 t로 가는 path의 집합

Alternate relational message passing

학습 과정은 다음과 같습니다.

$m_{v}^{i}=A_{1}(\lbrace s_{e}^{i}\rbrace_{e \in N(v)}),$

$m_{e}^{i}=A_{2}(m_{v}^{i},m_{u}^{i}), v, u \in N(e),$

$s_{e}^{i+1}=U(s_{e}^{i},m_{e}^{i})$

각 node에 대해 연결된 edge의 message를 aggregate하여 message을 생성합니다.
edge의 message는 양쪽 node의 message을 aggregate한 것으로 정의됩니다.
2번에서 얻은 message와 자신의 message를 통해서 message를 update합니다.

relational message passing에서는 인접한 모든 relation의 message를 결합했으나, 여기서는 relation의 양 끝 entity의 message만 결합하면 되므로 복잡도가 줄어들 것으로 생각됩니다. 이론적으로 Alternate relational message passing의 기대 복잡도가 $6M$임이 증명되었습니다.
지식 그래프는 relation의 수가 entity에 비해서 많이 적은 그래프이므로, 제안된 모델이 복잡도를 크게 낮춘 것을 확인할 수 있습니다.
다음은 모델에서 학습할 relation의 특징을 나타내는 구조에 대해 알아보겠습니다.

Relational Context

Relational Context는 entity에 연결되어 있는 모든 relation의 집합을 의미합니다.
예시는 다음과 같습니다.

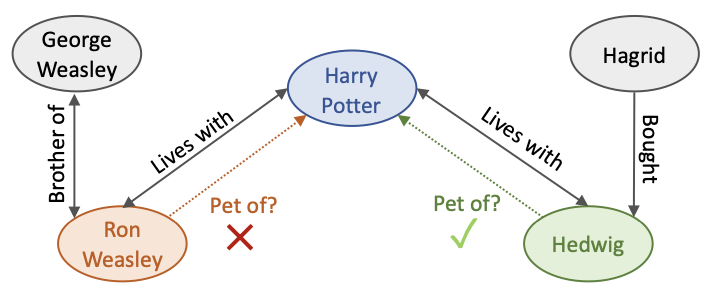
Ron Weasley와 Hedwig가 Harry Potter의 애완동물인지 예측하는 문제를 생각해봅시다.
두 Entity는 Harry Potter로 가는 경로가 {‘Brother of’,’Lives with’}로 같습니다.
그러나 Harry Potter와 인접한 relation이 각각 ‘Brother of’,’Bought’로 다릅니다.
따라서 Ron Weasley와 Hedwig은 서로 다른 relational context를 가집니다.
모델은 이를 파악해서 두 entity에 대해 적절한 예측 결과를 제공합니다.

Alternate relational message passing에서 relational context 학습 과정은 다음과 같습니다.

$m_{v}^{i}=\sum_{e \in N(v)}s_{e}^{i}$ $s_{e}^{i+1}=\sigma([m_{v}^{i},m_{u}^{i},s_{e}^{i}] \cdot W^i + b^i), \: v, u \in N(e)$

각 node에 대해 relational context의 feature를 학습합니다.
head, tail node와 relation의 정보를 결합합니다. 그리고 Weight를 곱해준 후 bias를 더하고 비선형 활성화 함수를 적용합니다.

이 과정을 K번 반복해 얻은 최종 message $m_{h}^{K-1}$와 $m_{t}^{K-1}$가 head, tail entity의 표현이 됩니다.

Relational Paths

Relational Path는 entity에서 entity로 갈때 거치는 relation의 sequence입니다.
예시는 다음과 같습니다.

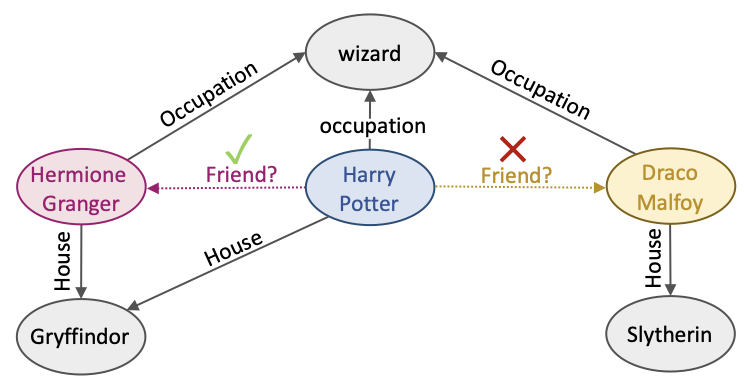
Hermione Granger와 Draco Malfoy가 Harry Potter와의 relation이 같은지 알아봅시다.
두 Entity는 같은 relational context {‘Occupation’,’House’}를 가집니다.
그러나 Harry Potter를 tail로 하는 relational path는 {(‘Occupation’,’Occupation’), (‘House’,’House’)}, {(‘Occupation’,’Occupation’)}로 다릅니다.
따라서 Hermione Granger와 Draco Malfoy는 Harry Potter와의 relation이 서로 다른 것을 알 수 있습니다.
모델은 이를 파악해서 두 Entity에 대해 Harry Potter와의 ‘friendship’ relation이 존재하는지 예측할 수 있습니다.

Relational context message passing은 node와 edge의 identity을 고려하지 않으므로, entity간의 상대적인 위치는 알 수 없습니다.
이 문제를 해결하기 위해 두 entity가 어떻게 연결됐는지 확인합니다. Relational Path는 경로 내 relation type의 sequence로 나타냅니다. 이때 각 path에서 거쳐가는 entity의 sequence는 유일합니다.
Notation은 다음과 같습니다.
$P = {r_{e_0},r_{e_1},…,r_{e_{L-1}}}$ : relation path
$P_{h \rightarrow t}$ : entity h에서 t로 가는 relation path의 set

이제 relation path의 표현을 정의하고 구해야 합니다. PATHCON은 각 path에 embedding vector를 할당합니다.
이렇게 되면 path의 수가 크게 늘어날 수 있으나, 실제 지식그래프는 relation의 밀도가 매우 낮으므로 문제되지 않습니다.
그러므로 relational path의 길이가 짧고 개수도 적다고 전제할 수 있습니다.

Model Framework

Combining Relational Context and Paths

PATHCON의 모델 학습 과정은 다음과 같습니다.

head, tail entity의 최종 정보를 통해 entity pair $(h,t)$ 의 context representation을 구합니다.
이때 실제 relation $r$은 예측 대상이므로, unobserved를 가정합니다.

$s_{(h,t)} = \sigma([m_{h}^{K-1}, m_{t}^{K-1}] \cdot W^{K-1} + b^{K-1})$
relational context representation이 포함된 Attention weight을 계산합니다.

$\alpha_{P}= \frac{exp((s_{P})^{\top} s_{(h,t)})}{\sum_{P \in P_{h \rightarrow t}} exp((s_{P})^{\top} s_{(h,t)})}$
path들의 중요도를 고려한 가중 평균을 구해 path의 representation을 얻습니다.

$s_{h \rightarrow t}=\sum_{P \in P_{h \rightarrow t}} \alpha_P s_P$
context representation과 더해서 softmax을 적용한 후 실제 relation와 predicted relation의 차이에 대해 cross entropy loss를 최소화하는 relation을 구합니다.

$p(r \vert h,t)=\text{SOFTMAX}(s_{(h,t)}+s_{h \rightarrow t})$ $\min L= \sum_{(h,r,t) \in D} J(p(r \vert h,t),r)$

Context representation $s(h,t)$는 predicted relation의 분포와 relation path의 중요도에 모두 큰 영향을 미치는 것을 확인할 수 있습니다.

Model Explainability

PATHCON은 relation만으로 모델링하므로 서로 다른 relation간의 관계를 파악하기 쉽습니다. 이로부터 예측 결과에 대한 explainability를 제공합니다.

1) relational context을 모델링하여 contextual relation과 predicted relation간의 상관관계를 파악할 수 있습니다.
이를 통해 주어진 relation의 중요한 이웃 relation을 나타낼 수 있습니다. 2) relational path을 모델링하여 path와 predicted relation간의 상관관계를 파악할 수 있습니다.
이를 통해 중요한 relational path을 나타낼 수 있습니다.

Design Alternatives

Context Aggregator

Mean aggregator relational context에서 concatenation 대신 mean을 사용해 통합합니다.
head와 tail의 순서가 바뀌어도 같은 결과를 제공합니다.
Cross aggregator
추천 시스템의 combinatorial features에서 가져온 아이디어이며, 과정은 다음과 같습니다.
1. Head와 tail의 message의 element-wise pairwise interaction을 계산합니다. $m_{v}^{i} (m_{u}^{i})^{\top}$
2. interaction matrix를 flatten하고, relational context와 동일하게 정보를 update합니다. $s_{e}^{i+1}=\sigma(\text{flatten}(m_{v}^{i} (m_{u}^{i})^{\top}) \cdot W_{1}^{i} + s_{e}^{i} \cdot W_{2}^{i} + b^i), v, u \in N(e)$
  이 방법은 입력한 node의 순서를 보존한다는 장점이 있습니다.

Relational Path learning

Learning path representation with RNN
path에 embedding을 거치지 않고 바로 RNN을 적용해 표현을 학습합니다.
모델의 Parameter의 수가 고정되고 relational path의 개수에 영향을 받지 않는 장점이 있습니다.
또한, 경로 간의 유사성을 파악할 수 있을 것으로 기대됩니다.

Path Aggregator

Mean path aggregator: relational path에서 attention weight 대신 mean을 적용해 통합합니다.
Relational context의 표현을 사용할 수 없을 때 대체하기 위해 사용합니다.

4. Experiment

Experiment setup

Dataset
지식 그래프 Dataset인 FB15K, FB15K-237, WN18, WN18RR, NELL995, DDB14을 사용하였습니다.
summary는 아래와 같습니다.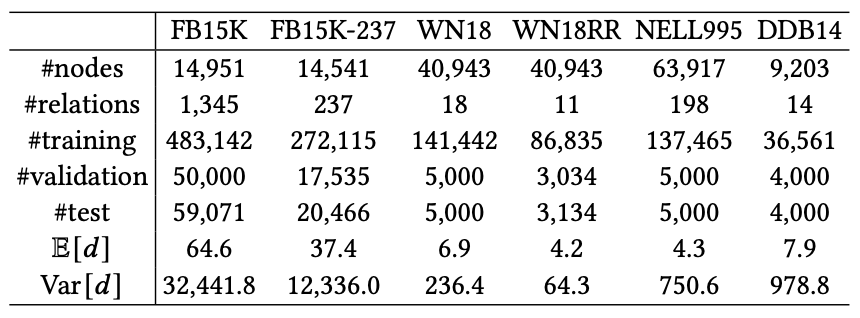

각 Dataset의 Parameter의 수는 다음과 같습니다.
Baseline
TransE, ComplEx, DistMult, RotatE, SimplE, QuitE, DRUM, CON, PATH
Relational Context, Relational Path 중 하나만 적용한 모델 CON, PATH을 추가해 각각의 효과를 확인하고자 합니다.
Evaluation Metric
MRR(Mean Reciprocal Rank)
Hit@1,3 : cut-off value가 1, 3인 Hit Ratio
Result
Overall Results

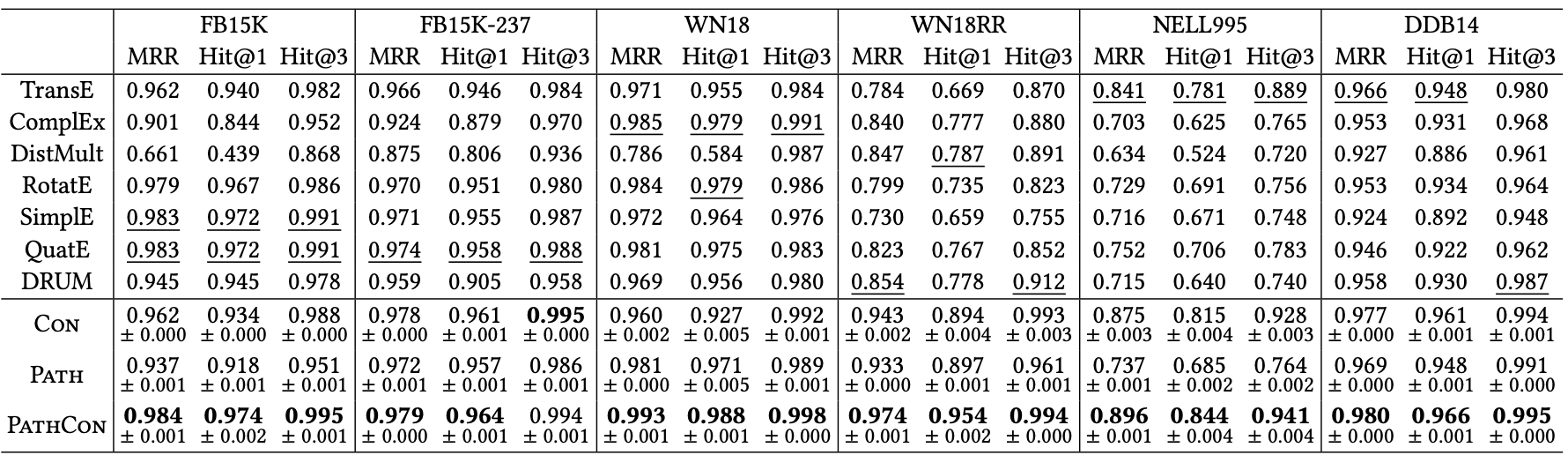
PATHCON이 모든 경우에서 기존 baseline보다 성능이 뛰어나며 특히 sparse 데이터에서 강점을 보입니다.
한편 PATH, CON 모델에서도 대체로 다른 baseline보다 성능이 뛰어난 것을 확인할 수 있습니다.
이로부터 relational path, relational context가 각각 성능 향상에 기여하는 것을 알 수 있습니다.
Inductive Knowledge Graph Completion

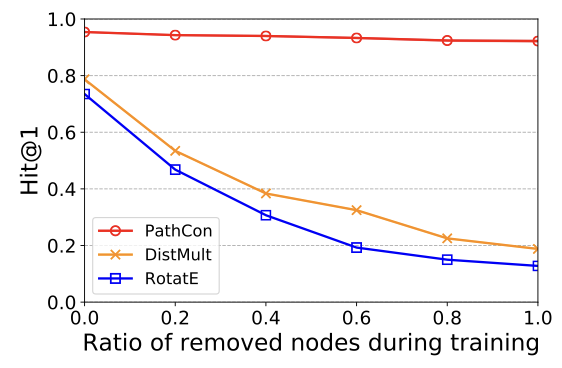
PATHCON의 주요 contribution 중 하나인 inductive setting에서의 performance에 대한 결과입니다. 차트의 가로축은 test set의 entity subset 중에서 train set에 포함되지 않은 entity의 비율이며 값이 클수록 inductive setting에 가까워집니다.

Embedding 기반의 baseline은 학습하지 않은 데이터에 대해 예측하는 비율이 높아질수록 성능이 떨어지는 반면, PATHCON의 성능은 setting에 robust합니다.
이로부터 PATHCON이 inductive setting에 적합한 모델임을 알 수 있습니다.

Model Variants

Context Hops / Path Length
Relational Context와 Path Length의 sensitivity를 확인합니다.

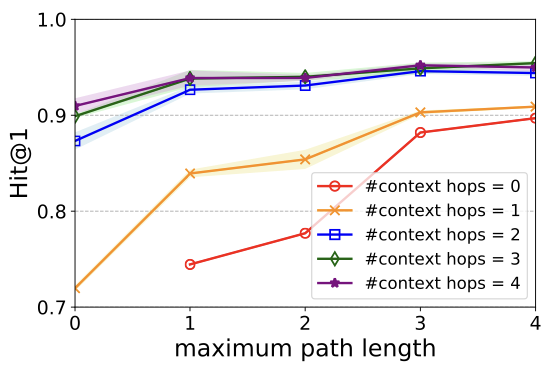
relational context와 path length의 값이 커짐에 따라서 성능이 향상됨을 알 수 있습니다. 이를 통해 context에 더 많은 정보를 포함하는 것과 path의 길이가 학습에 중요하다는 것을 알 수 있습니다. 두 structure 모두 값이 커질수록 성능 향상폭이 작아집니다.

Context Aggregator
context aggregator를 바꿔가면서 성능을 비교하였습니다.

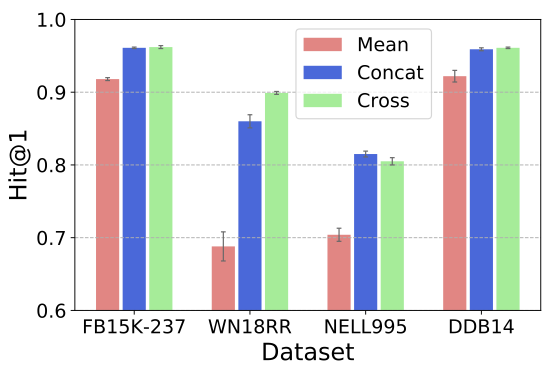
mean aggregator의 성능이 가장 나쁘므로, 특징을 결합할 때 entity의 순서가 중요한 것을 확인할 수 있습니다.
concat과 cross은 데이터에 따라 상대적인 성능이 달라지지만, cross의 parameter가 더 많으므로 학습 시간이 길어집니다.
데이터의 특성에 더 적합한 aggregator를 선택해야 합니다.

Path Representation

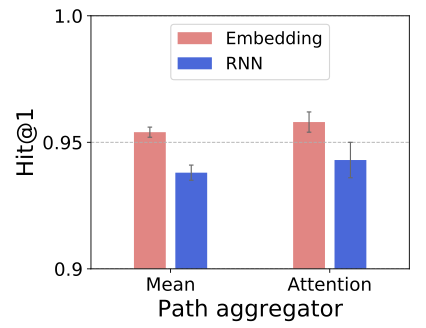
relation type과 relation aggregator에 따라 성능을 비교합니다.
relation type을 embedding으로 나타낼 때 RNN보다 성능이 뛰어났는데, 이는 전체 지식 그래프의 relation density가 낮아서 relation path가 대체로 짧기 때문인 것으로 생각됩니다.
또한 attention이 mean보다 좋은 aggregator임을 확인할 수 있으며, relation path의 중요도를 고려해서 모델을 학습해야 함을 알 수 있습니다.
Model Explainability
모델이 예측 결과를 얼마나 잘 설명하는지에 대해 알아보고자 합니다.

실험 과정은 다음과 같습니다.
1) context hop $=1$, path length $\leq 2$로 설정합니다. 2) 학습이 완료된 상태에서 3개의 relation을 선택합니다. 3) 각 relation에 대해 가장 중요도가 높은 relational context와 path를 제시합니다.

제시된 결과를 보면, relational context와 path의 내용이 relation과 문맥상 의미가 통하는 것을 알 수 있습니다.
이를 통해 모델이 예측한 relation에 대해 explainability를 제시한다고 할 수 있습니다.

5. Conclusion

본 논문은 지식 그래프 완성 문제를 해결하기 위해 기존의 연구들과 달리 relation path를 기반으로 했습니다.
relation에 대한 message passing을 적용하였고, 정보 통합 과정을 수정해서 복잡도를 낮추는 alternate relational message passing을 제안하였습니다.
Alternate relational message passing의 강점인 inductive setting, storage efficiency, model explainability를 확인하였습니다.
지식 그래프의 subgraph 구조인 relation context와 relation path가 모두 모델의 성능을 높이는 요인임을 확인하였습니다.
sparse한 지식 그래프에서도 성능을 유지하는 것을 보였습니다.

Review

message passing을 활용하는 대부분의 기존 GNN 모델은 node feature에 초점을 맞추고 있습니다.
그러나 본 논문에서는 edge feature에 message passing을 적용해서 학습하는 프레임워크를 제시하였습니다.
message passing 개념이 나옴에 따라 생각해볼 만한 아이디어였지만, 실제로 구현되었다는게 신기했습니다.
여기서 더 나아간다면, 화학이나 생명공학처럼 개체 그래프의 node feature와 edge feature가 모두 중요한 도메인에 대해 이 논문의 아이디어를 적용할 수 있을 것입니다.

Author Information

Author name
김대영 (Daeyoung Kim)
Affiliation
KAIST ISysE HS Lab
Research Topic
Application of statistics

6. Reference & Additional materials

Github Implementation
(https://github.com/hwwang55/PathCon)
Reference
[KDD ‘21] Relational Message Passing for Knowledge Graph Completion (https://arxiv.org/pdf/2002.06757.pdf)
지식 그래프의 정의 (https://www.samsungsds.com/kr/insights/techtoolkit_2021_knowledge_graph.html)