[CIKM 2023] Region Profile Enhanced Urban Spatio-Temporal Prediction via Adaptive Meta-Learning

Info

Authors: Jie Chen, Shanghai University
Key words: Urban spatio-temporal prediction; Meta-learning; Deep learning
Paper Links

1. Problem Definition

Background 도시 센싱 기술과 모바일 컴퓨팅의 빠른 발전은 지능형 도시 구축을 크게 촉진하였다. 그 중 도시 공간-시간 (Spatio-temporal, ST) 예측은 가장 주목받는 스마트 도시 서비스 중 하나로, 궤적 예측, 경로 시간 추정, 출발지-목적지 수요 예측과 같은 다양한 도메인의 응용을 가능하게 한다. 예를 들어, 업무지구는 주로 평일 오전과 저녁에 사람들이 몰리는 반면, 주거 지역은 주말에 더 활발할 수 있다는 점을 활용한다면, 해당 지역의 사람들의 궤적을 예측하거나, 사람들의 경로에 대한 시간을 추정하는 등의 서비스로 이어질 수 있다. 따라서, 정확한 ST 예측 시스템은 스마트 도시 서비스의 효율성을 향상시키고, 비상 상황에 대한 조기 경고를 제공하며, 정책 결정에 필요한 통찰을 제공하는 중요한 역할을 제공할 수 있다.

Problem 이 논문에서는 각 지역에서 수집할 수 있는 데이터가 한정적인 상황에서 어떻게 효과적인 ST 예측을 수행할 수 있는지에 대해 초점을 맞추고 있다.

2. Motivation

Challeng of ST prediction 기존의 하이브리드 딥러닝 모델들은 ST 예측을 높은 성능으로 수행하고 있다. 하지만, 이러한 모델들은 대규모 훈련 데이터에 의존하고 있기 때문에 각 지역의 데이터 수집이 어렵고, 수집된 데이터 또한 불안정할 수 있는 실제 도시 환경 상황에는 알맞지 않다는 한계점이 존재하였다. 그래서 최근에는 데이터가 부족한 시나리오에서도 예측이 가능한 고급 메타러닝 방법을 ST 예측 task에 사용하는 연구가 증가하고 있는 추세이다. 그런데, 지금까지의 연구들은 학습을 할 때 지역 간의 내제되어 있는 차이로 인해 발생되는 부정적인 transfer를 피하지 못한다는 한계점이 있었다. 예를 들어, Figure1과 같이 두 다른 지역에 일정 부분이 거의 일치하는 ST 역학을 보일 때(예: 아침, 저녁 피크), 지역간에 차이가 있음에도 불구하고 유사하게 관찰된 ST 역학에 동일한 클러스터링 메타 전략이 적용되는 상황이 발생한다는 것이다.

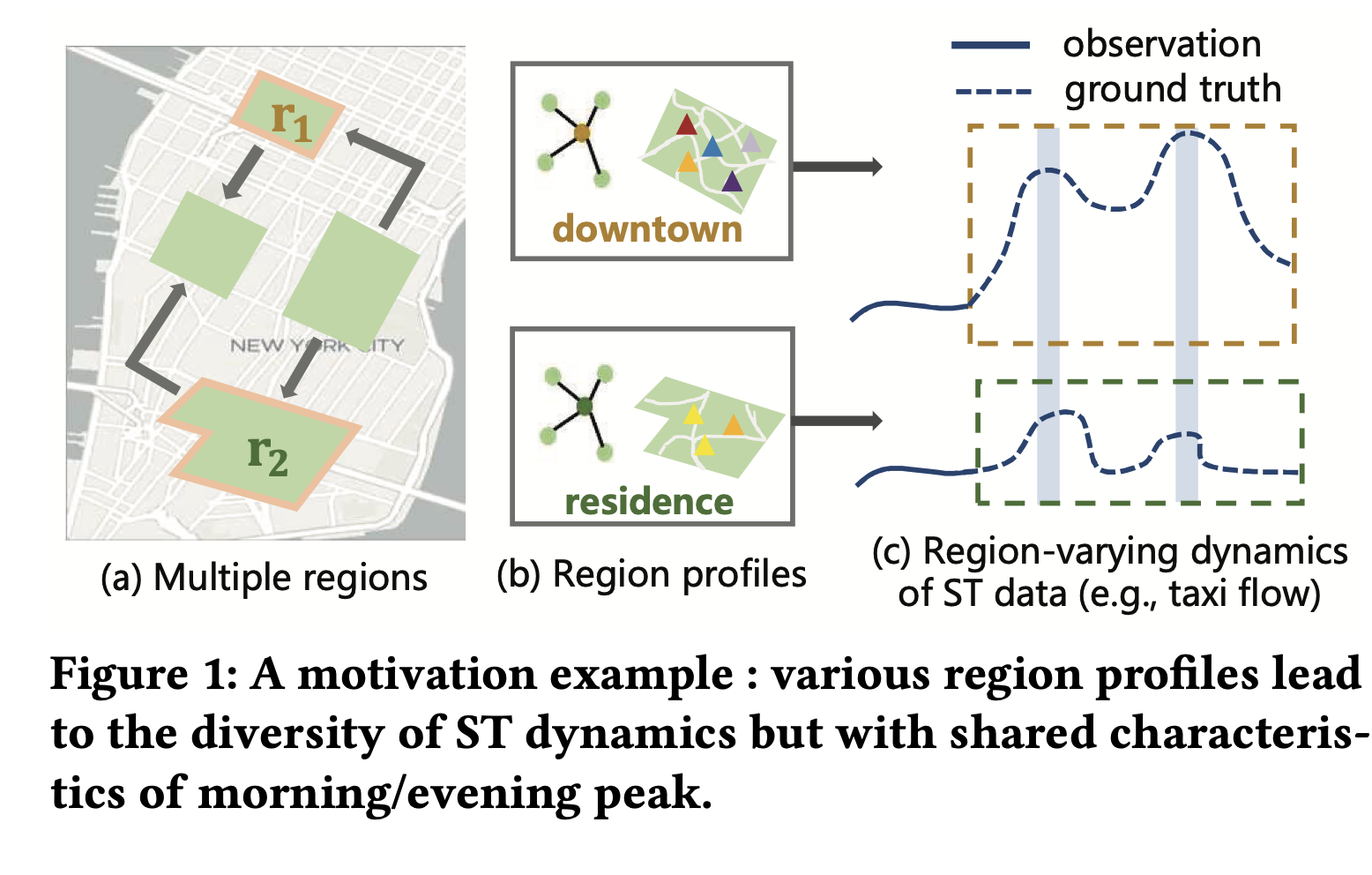
Proposed Idea 이 논문에서 제안하는 MetaRSTP 모델은 기존연구의 한계점을 극복할 수 있도록 지역간 이동성과, 지역내 특징을 활용하여 지역 프로필을 추출하는 새로운 임베딩 방식을 사용하였다. 또한, regional bias generator를 활용해 프로파일에 관한 비공유 파라미터를 도출하여 지역간의 차이를 완화하였다. 저자는 고정된 generalizable parameter와 region-adaptive bias로 네트워크를 초기화 하는 새로운 메타러닝 전략을 설정함으로써, 데이터가 적은 시나리오에서도 성능이 강화할 수 있도록 모델을 설계하였다.

저자들이 제시한 이 새로운 메타러닝 전략은 각 지역의 특수성을 고려하여 개인화된 지역의ST 예측 성능을 향상시킬 뿐만 아니라, 데이터가 부족한 환경에서도 높은 예측 정확도를 제공할 수 있도록 도왔다.

3. Preliminary

3.1. Problem Formulation

저자들은 이전 연구에 따라 도시들을 $N_R$ 개의 독립적인 지역들로 나누고, $R = {r_1, r_2, \ldots, r_{N_R}}$ 로 표현했다. 그리고 아래와 같은 5개의 ST 예측에 필요한 개념 5개를 정의하였다.

Definition1. Inter-Region Mobility View 는 지역 간의 상호작용을 표현한다. 이 뷰는 다양한 지역 간의 원산지와 목적지(OD) 데이터를 통해 이동 패턴을 수치적으로 표현하고, 각 지역 간의 연결 강도를 파악한다.

따라서, 지역 $r_i$에 대한 OD(원산지-목적지) 맥락은 아래의 두가지 분포로 표현된다.

출발 확률 분포 $p_o(r_k \mid r_i)$: 지역 $r_i$ 에서 출발하여 지역 $r_k$ 로 도착하는 상대적 이동성 확률을 나타낸다.
$p_o(r_k \mid. r_i) = \frac{w(r_k, r_i)}{\sum_{r_j} w(r_j, r_i)}$
도착 확률 분포. $p_d(r_k \mid r_i)$: 지역 $r_i$ 로 도착하는 이동성 확률 중에서 지역 $r_k$ 에서 출발한 비율을 나타낸다.
$p_d(r_k \mid r_i) = \frac{w(r_ {i}, r_ {k})}{\sum_ {r_ {j}} w(r_ {i}, r_ {j})}$

위에서 사용된, 이동 가중치 $w(r_i, r_j)$ 는 지역 $r_i$ 에서 지역 $r_j$ 로의 여행 발생 횟수를 나타내는 수치이다. 이 수치는 다음과 같이 계산된다.

$w(r_ {i}, r_ {j}) = \vert (r_ {o}, r_ {d}) \in M \mid r_ {o} = r_ {i}, r_ {d} = r_ {j} \vert$

여기서 $\vert \cdot \vert$는 집합 내 원소의 개수를 세는 연산으로, 특정 조건을 만족하는 여행 쌍의 발생 빈도를 계산한다. 즉, 지역 $r_ {i}$ 에서 출발하여 지역 $r_ {j}$ 로 도착하는 모든 여행 쌍 $(r_ {o}, r_ {d})$ 의 개수를 세어 이동성 가중치를 결정한다.

Definition2. Intra-Region Geospatial View는 각 지역의 지리적 특성을 관심 지점(POI)의 분포 p와 도로 네트워크 density d로 나타낸다. ($f={p,d}$) 이것은 지역의 기능과 속성을 나타낼 수 있다. p에 있는 차원은 대응하는 POI의 카테고리의 비율을 나타내고, d에 있는 차원은 면적을 도로 길이로 나눈 값으로 계산된다.

Definition3. Region profile는 타겟 지역의 이동성 패턴과 지리적 특성에 기반한 지역 프로필을 학습하여, 각 지역을 포괄적으로 설명할 수 있는 임베딩을 생성 (E=${e_{r_i}}$)한다.

Definition4. Urban Dynamic State 도시 ST데이터는 도시 ST 데이터에는 택시 수요, POI 체크인 등이 포함되며, 공간적으로 변화하고 시간에 따라 진화한다. 그래서, 저자는 시간 범위를 동일한 길이의 시간 슬롯으로 나누고, 각 지역에서의 동적 상태(e.g., 택시 픽업 횟수)를 해당 시간 슬롯에서 나타낸다.

Definition5. Urban ST Sequence 지리학의 첫 번째 법칙에 따라, 인접 지역들은 자연스럽게 명시적인 공간 의존성을 나타낸다. 특정 시간 슬롯 $t$ 에서, 지역 $r_i \in R$ 는 벡터 $x_{r_ {i}}^{(t)} = [x_{r_ {k}}^{(t)}] \in \mathbb{R}^{N_ {S}}$ 와 관련되어 있는데, 이 벡터는 지역 $r_i$ 와 그 공간적 이웃 지역들 (자기 자신을 포함하여 다른 $N_S - 1$ 지역들)의 도시 상태를 집약하여 나타낸다. 이러한 공간적 특성을 연속적인 시간 슬롯 $T$ 에 걸쳐 수집함으로써, 저자는 도시 ST 시퀀스를 $S_{r_i} = [x_{r_i}^{(t)}]_{t=t_c-T}^{t=t_c} \in \mathbb{R}^{T \times N_S}$로 표현하는데, 여기서 $t_c$는 마지막 시간 슬롯이다.

Problem Formalization. 저자들은 이렇게 5가지의 개념을 정의한 뒤, 지역 $r_i$ 에 대하여 $T$ 개의 과거의 동적 특성과 해당 지역 프로필 $e_{r_i} \in E$ 이 주어졌을 때, 다음 도시 상태를 예측하기 위한 함수 $f_{\phi_{r_i}}(\cdot)$ 를 학습하는 모델을 구성하였다:

$f_{\phi_{r_i}}([S_{r_i}; e_{r_i}]) \rightarrow y_{r_i}^{(t+1)}$

여기서 $y_{r_i}^{(t+1)}$ 는 실제 값이며, $f_{\phi_{r_i}}(\cdot)$는 $\phi_{r_i}$ 로 파라미터화된 특정 예측 신경망이다.

3.2. Meta-Learning setting

메타 러닝은 다양한 학습 task들 간에 공통적인 지식을 추출하고, 이를 새로운 task에 빠르게 적용하여 효과적인 학습을 가능하게 하는 방법이다. 이 연구에서는 지역 수준의 ST 예측을 하나의 학습 task로 간주하는 메타 러닝을 사용했으며, 각 task는 model-agnostic meta-learning(MAML) 기반의 학습 setting에 따라 관측된 데이터를 토대로 support set와 query set로 나뉜다, i.e., $T_{ri} = {D_{ri}^{sp}, D_{ri}^{qr}}$. 전자는 local-update 동안 초기 네트워크를 미세 조정하는데 사용되며, 후자는 global-update 동안 일반화된 초기 네트워크를 학습하는데 사용된다. 적은 수의 샘플을 가진 시나리오와 일반 시나리오를 모방하기 위해 샘플 수를 조정함으로써, 강력한 적응력을 가진 예측 모델을 얻기 위한 훈련 task의 배치가 샘플링 된다.

4. Method

저자들은 지역 프로필을 활용한 adaptive meta learning 프레임워크, MetaRSTP를 만들 때 1. 포괄적인 지역 특성을 뽑아낼 수 있도록 하는 지역 프로필을 뽑는 것과 2. 추출된 지역 프로필을 기반으로 negative noise를 제외하고 extra region semantics을 포함할 수 있는 메타러닝을 개발하는 것을 목표로 모델을 구성하였다.

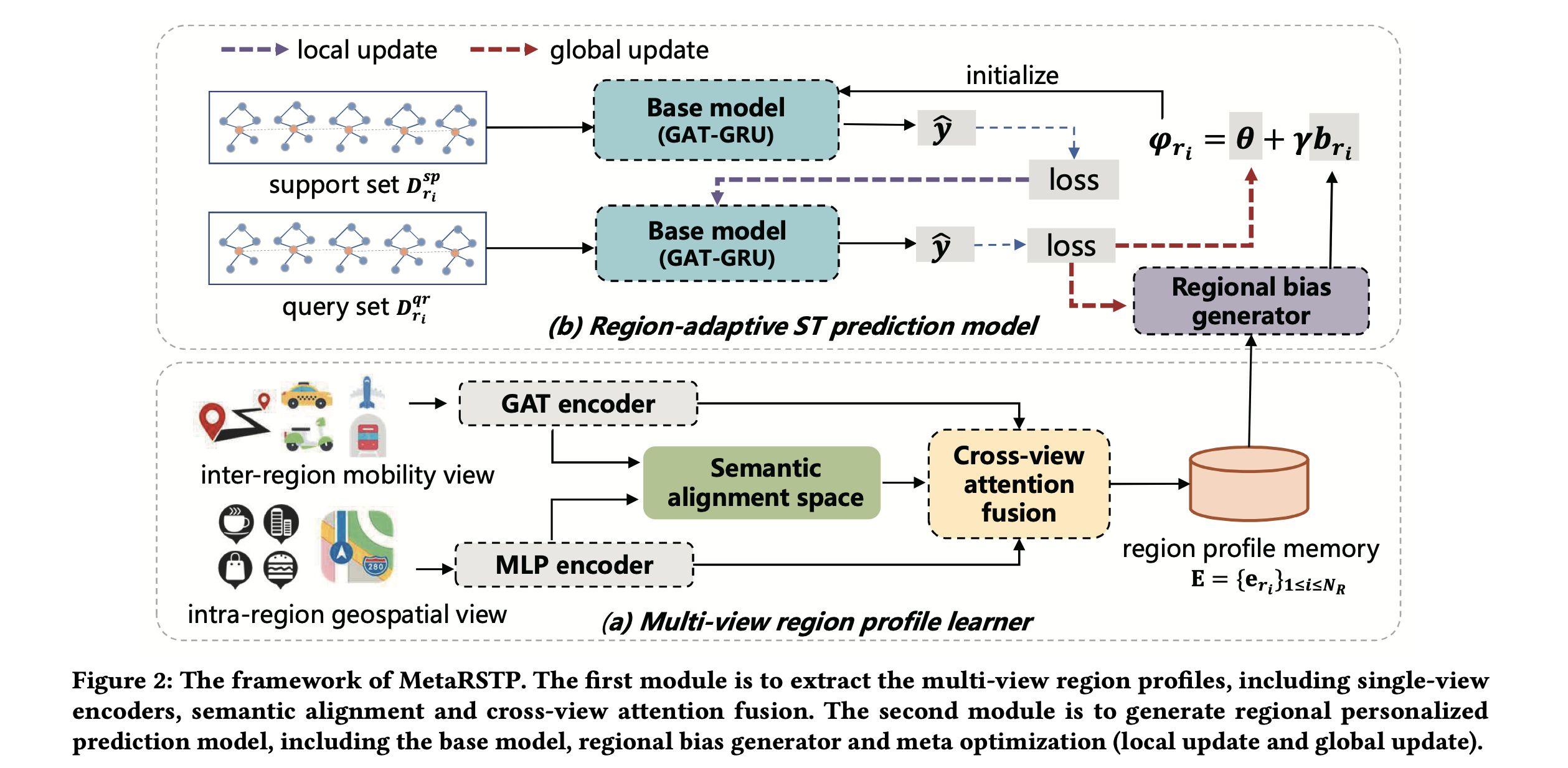
위 그림은 저자가 제시한 MetaRSTP의 모델 아키텍쳐이다.

1. multi-view region profile learner

포괄적인 지역 특성을 뽑아낼 수 있도록 하는 지역 프로필을 뽑기 위해서, 저자들은 위 그림의 (a) 구조를 제안하였다. 자세한 설명은 아래와 같다.

[1] 두개의 single view를 통한 지역 임베딩. 저자는 지역간의 mobility view와 지역 내의 geospatial view, 즉 두 개의 single-view encoders를 별도로 구현하여 차별화된 특성 추출을 수행하였다.

mobility view에서는, 동일한 original distribution이나 destination distribution을 가지는 지역들을 도시의 function에 대한 힌트를 서로 줄 수 있는 가까운 사이로 간주하였다. 이때, 코사인 유사도가 상위 $N_M$인 지역과 연결 하였는데, 지역간 이동성은 그래프를 통해 구축하였다. 지역의 mobility correlation을 임베딩에 통합하기 위해 Graph Attention Network, GAT를 사용하였으며, 이때 지역 간의 원산지-목적지(OD) 연결성을 기반으로 attention score을 계산하였다. 이후, 이 score를 가지고 이웃들로부터 정보를 전파하여 각 region의 representation을 업데이트하였다.

각 지역 $r_i$와 연결된 지역 $r_j$에 대해, 다음과 같이 attention Score를 계산하였다:

$\alpha_ {ij}^{m} = \frac{\exp(\text{LeakyReLU}(a_ {m} [W_ {m} v_ {i} | W_ {m} v_ {j}]))}{\sum_{k \in N_ {\epsilon m}[r_ {i}]} \exp(\text{LeakyReLU}(a_ {m} [W_ {m} v_ {i} | W_ {m} v_ {k}]))}$

그리고, 계산된 attention score를 가지고 region embedding을 업데이트 하였다:
$e_ {r_i}^{m} = \sum_ {j \in N_ {\epsilon m}[r_ {i}]} \alpha_ { ij}^{m} \Phi_ {m } v_ {j}$

이때, $W_{m}, \Phi_ {m}, a_ {m}$ 은 학습 파라미터이다.

한편, geospatial view에서는 coarse POI와 road density feature를 $e_ {r_{i}}^{g}$로 변환하는데, MLP를 사용하였다.

[2] 두 view를 통해 나온 지역 임베딩으로 부터 semantic alignment space 설계.
저자는 두 view간에 semantic constraint을 다루고, co-semantic을 밝히는 semantic alignment space 을 구축하였다. 저자는 한 지역의 두 view의 specific 특징이 동일한 기저 지역 패턴을 반영하기 때문에 서로 일치할 수 있다는 직관적인 생각을 바탕으로 space를 설계하였다. 예를 들어, 중심 지역의 경우 광범위한 지역과의 mobility correlation은 높은 도로 밀도와 다중 유형 POI 분포와 일치한다는 것이다.

그래서, 저자는 contrastive learning에서 영감을 받아 co-semantic representation을 구축할 때 Noise Contrastive Estimation (NCE) 목적 함수를 통해 positive pair를. negative pair와 비교하는 방식을 사용하였다. 구체적으로 설명하자면, 지역 $r_i$ 에 대해, mobility view의 임베딩과 geospatial view의 임베딩이 서로 ground-truth가 되며, positive pair $(e_ {r_ {i}}^{m}, e_ {r_ {i}}^{g})$으로 간주 되어졌다. 그리고 다른 지역들의 view 임베딩을 샘플링 함으로써, {$(e_ {r_ {i}}^{m}, e_ {r_ {n}}^{g})$, $(e_ {r_ {n}}^{m}, e_ {r_ {i}}^{g})$} , $n \neq i$ 과 같은 negative pair을 정의하였다.

이후, 모든 가능한 pair of ($e^{m}$,$e^{g}$)가 서로 매핑될 수 있도록 아래와 같은 alignment 절차를 수행하였고, 이것이 최종적으로 학습하고 싶은 co-semantics 지역 프로필이 된다:
$ê_{c} = \text{Align}(e^ {m}, e^ {g}) = \text{ReLU}(W([e^ {m} \Vert e^{g}] + b))$

이때, 서로 다른 지역의 inter-view를 matching할 때는 positive co-semantic representations를 잘 확보하기 위해서 InfoNCE loss function을 사용하였는데 관련 수식은 아래와 같다.

$\mathcal{L}_ {\text{inter}} = \sum_{r_ i \in R} \left[ -\log \mathcal{M}(e_ {r_ i}^m, e_ {r_ i}^{g}) + \left( \log (\mathcal{M}(e_ {r_ i}^{m}, e_ {r_ {i}}^{g}) + \sum_ {e_ {r_ n}^{m} \in \hat{E}^{m}} \mathcal{M}(e_ {r_ {n}}^{m}, e_ {r_ {i}}^{g}) + \sum_ {e_ {r_ {n}}^{g} \in \hat{E}^{g}} \mathcal{M}(e_ {r_ {i}}^{m}, e_ {r_ {n}}^{g})) \right) \right]$

여기서 $\mathcal{M}(\cdot, \cdot) = \exp(\text{Align}(\cdot, \cdot))$은 view별 특정 지역 임베딩 간의 매칭 점수를 평가하기 위해 inter-vew discriminator로 작동한다. 모델 학습 후, $r_i$ 의 real co-positive semantics $e_ {r_ {i}}^{c} = \text{Align}(e_ {r_ i}^{m}, e_ {r_ {i}}^{g})$ 은 학습되고 활용된다.

[3] Cross-view Attention Fusion로 지역 임베딩 통합
저자는 마지막으로, cross-view attention 매커니즘으로 view간의 co-semantics와 view들 각각에 있는uniqueness를 fusion하여 지역 프로파일링의 표현력을 강화하였다.

이때, co-semantic 임베딩 ( $E^{c} = {e^{c}}$ )은 key로 간주되며, 모든 임베딩은 query로 사용하였다. 그리고, 다음과 같이 키 행렬 $K$ 와 쿼리 행렬 $Q^{*}$ ($* \in {m, c, g}$)를 다음과 같이 연관시켰다:

$K = E^{c} W_ {k}, \quad Q^{*} = E^{*}W_ {q}.$

여기서 $W_ {k}$와 $W_ {q}$는 학습 가능한 매개변수이다.

그런 다음, 아래와 같이 single view를 co-semantic view와 융합하여 최종 지역 표현 E를 얻었다:

$A^{*} = \text{softmax} \left( \frac{ Q^{*} K^{T} }{\sqrt{D_ {R}} } \right), \quad E = A^{m} E^{m} + A^{c} E^{c} + A^{g} E^{g}$

이 $E = {e}$ 는 co-semantic과 뷰별 uniqueness을 합쳐서 종합적인 특징을 포함하는 지역 프로파일링이다.

[4] Training objective
위의 1,2,3을 잘 수행할 수 있도록, 저자는 아래와 같이 adjustable weights $\beta_{1},\beta_{2}, \beta_{3}$을 갖는 아래의 Loss를 설계하였다:
$L_{emb} = \beta_ {1} L_{mob} + \beta_ {2} L_ {inter} + \beta_ {3} L_ {geo}$

첫째로, $L_ {mob}$은 지역 프로필 $e_ {i}$, $e_ {j}$가 있는 지역 $r_ {i}$, $r_ {j}$에 대한 전이 확률을 추정할 수 있다라는 것을 토대로, 아래와 같은 loss를 정의하였다:
$L_ {mob} = \sum_ {(r_ {i}, r_ {j}) \in R} -p_ {o}(r_ {j} | r_ {i}) \log \hat{p}_ {o}(r_ {j} | r_ {i}) - p_ {d} (r_ {j} | r_ {i}) \log \hat{p}_ {d} (r_ {j} | r_ {i})$

이때, 추정된 전이확률은 다음과 같다. $\hat{p}_ {o}(r_ {j}|r_ {i}) = \frac{\exp(e_ {r_i}^T e_ {r_ {j}})}{\sum_k \exp(e_ {r_ {i}}^T e_ {k})}$

둘째로, $L_{inter}$는 위에서 설명했던 infoNCE loss function를 활용하였다.
$L_ {inter} = \sum_ {r_ {i} \in R} \left[ - \log M(e_ {r_ {i}^m }, e_ {r_ {i}}^{g}) + \log \left( M(e_ {r_ {i}}^{m}, e_ {r_ {i}}^{g}) + \sum_ {e_ {r_ {n}}^m \in \hat{E}^{m}} M(e_ {r_ {n}}^{m}, e_ {r_ {i}}^{g}) + \sum_ {e_ {r_{n}}^{g} \in \hat{E}^{g}} M(e_ {r_ {i}}^{m}, e_{r_{n}}^{g}) \right) \right]$

셋째로, $L_ {geo}$는 학습된 지역 프로필이 지역 특성 측면에서 지역 유사성을 보존한다는 점을 활용해, 지역 프로필을 기반으로 지역 상관 관계를 재구성하는 방식을 이용했다:
따라서, loss는 $c_{geo}(r_ {i}, r_ {j}) = \text{CosSim}(f_ {r_ {i}}, f_ {r_ {j}})$를 라벨로 사용하여, $L_ {geo} = \sum_ {(r_ {i}, r_ {j}) \in R} (c_ {geo}(r_ {i}, r_ {j}) - e_ {r_ {i}}^{T} e_ {r_ {j}})^{2}$로 정의된다.

2. Region-Adaptive ST Prediction Model

저자는 추출된 지역 프로필을 기반으로 negative noise를 배제하는 region-adaptive ST prediction model을 제시하였다 (Figure의 (b)부분). 저자들은 특정 지역에 대해 biased initialization을 customize하는 혁신적인 방식을 제시한다. 구체적으로, 지역 프로필이 input으로 들어 왔을 때, region bias generator가 prediction model안에서 personalized bias를 제공는 것을 목표로 한다. 저자들은 local and global update를 통해 common ST regularity를 나타내는 fixed shared parameter과 함께 최종적으로 생성된 initial network로 더 세분화된 지역 수준의 few-shot task을 수행하는 모델을 제시한다.

[1] Base mode
저자는 과거의 도시 시공간 ST 시퀀스를 기반으로 다음 도시 상태를 예측하도록 설계된 model을 base model로 사용했다. 이 모델은 도시 내 dynamics(역학)에 내재된 복잡한 ST dependency를 모델링하는 것을 목표로 한다. 모델링 할 때, 인접 지역은 상호 영향을 미치며, 지역의 이전 상태는 후속 상태에 영향을 주도록 했다.

저자는 지역간의 공간적 상관관계를 모델링하기 위해 GAT(Graph Attention Network)를, 해당 지역의 시간적 변화를 캡처하기 위해 GRU(Gated Recurrent Unit)를 사용하여 하이브리드 GAT-GRU 모델을 구축했다.

공간적 상관관계를 모델링하기 위해, GAT를 사용하여 특정 지역 $r_{i}$에 대해서 거리 기반으로 선정된 인접 지역 노드와의 attention score $\alpha_ {ij}^{s}$ 를 계산하였다. 다음으로 계산된 attention score를 이용하여, 지역 $r_{i}$ 를 인접 지역간의 관련성으로 공간적으로 표현한 $z_ {r_i}^{(t)}$로 나타내었다. 즉, $z_ {r_i}^{(t)}$ 는 인접한 지역들과 해당 지역간의 관계를 나타내는 $\alpha_ {ij}^{s}$ 을 가중치로 사용하여 summation하는 방식으로 구해진다. 아래는 관련 수식이다.

$\alpha_ {ij}^{s} = \frac{\exp(\text{LeakyReLU}(\mathbf{a}_ s [\mathbf{W}_ s \mathbf{x}_ {r_ i}^{(t)} \vert\vert \mathbf{W}_ s \mathbf{x}_ {r_ j}^{(t)} ]))}{\sum_ {k \in \mathcal{N}_ {\epsilon^{s}}[r_ i]} \exp(\text{LeakyReLU}(\mathbf{a}_ s [\mathbf{W}_ s \mathbf{x}_ {r_ i}^{(t)} \vert\vert \mathbf{W}_ s \mathbf{x}_ {r_ k}^{(t)} ]))}$

$\mathbf{z}_ {r_ i}^{(t)} = \sum_ {j \in \mathcal{N}_ {\epsilon^{s}}[r_ i]} \alpha_ {ij}^{s} \mathbf{\Phi}_ s \mathbf{x}_ {r_ j}^{(t)}$

이때, $W_ {s}, \Phi_ {s}, a_ {s}$ 은 학습 파라미터이다.

시간적 변화를 모델링하기 위해 GRU를 통해 모든 공간 표현을 시간 범위 ${t_ c - T, \ldots, t_ c}$ 동안 전달하며 다음과 같은 방식으로 공식화 하였다.

$\mathbf{u} = \sigma(\mathbf{W}_ u \mathbf{z}_ {r_ i}^{(t)} + \mathbf{U}_ u \mathbf{h}_ {r_ i}^{(t-1)} + \mathbf{b}_ u)$

$\mathbf{r} = \sigma(\mathbf{W}_ {r} \mathbf{z}_ {r_ {i}}^{(t)} + \mathbf{U}_ {r} \mathbf{h}_ {r_ i}^{(t-1)} + \mathbf{b}_ r)$

$\mathbf{h}_ {r_ i}^{\prime (t)} = \phi(\mathbf{W}_ h \mathbf{z}_ {r_ i}^{(t)} + \mathbf{U}_ h (\mathbf{r} \circ \mathbf{h}_ {r_ i}^{(t-1)}) + \mathbf{b}_ h)$

$\mathbf{h}_ {r_ i}^{(t)} = \mathbf{u} \circ \mathbf{h}_ {r_ i}^{(t-1)} + (1 - \mathbf{u}) \circ \mathbf{h}_ {r_ i}^{\prime (t)}$

여기서 $\mathbf{z}_ {r_ i}^{(t)}$, $\mathbf{h}_ {r_ i}^{(t)}$ 는 각각 시간 $t$ 에서의 input vector이고, hidden vector이다. $\mathbf{u}$ 와 $\mathbf{r}$ 는 각각 update gate vector와 reset gate vector이다. W는 weight metric이고, b는 bias이며 $\circ$ 는 element-wise multiplication이다.

저자는 GRU의 ouput $\hat{y}_{r_i}^{(t+1)}$는 시간 t+1에서 지역 $r_i$의 다음 상태를 예측하는 값으로 사용하였다.

[2] Regional Bias Generator
Urban planning에서 ST dynamics는 지역 프로필과 관련이 깊다. 예를 들어, 교통 패턴이 비즈니스 센터와 산업 단지가 완전히 다른 상황 등이 있다. 현존하는 meta-learning 방식은 training task로부터 shared knowledge를 뽑아서 사용하는데, 이는 target task에 fitting할 때 부정적인 transfer를 일으킬 수 있다. 이것을 해결하기 위한 방식으로 가능성 있는 approach는 다른 지역들로부터 생기는 차이를 다루기 위해 고유의 지역 features로써 indicative weighted bias를 사용하는 것이다.
그래서, 저자는 Regional Bias Generator를 제시하여 각각의 지역에 bias를 할당할 수 있도록 하였다. 이 과정에서 사용된 인사이트는 지역 프로필을 특정 ST correlation을 포착하기 위한 ST prediction neural network의 중요한 metadata로 보는 것이다.

저자는 지역 $r_i$에 대해서, 해당 지역 임베딩 $e_ {r_ {i}}$를 지역 프로필 메모리 $E$에서 검색하도록 했다. Regional Bias Generator는 이 지역 프로필을 input으로 사용하여 non-shared bias parameter $b_ {r_ {i}}$를 output으로 내보낸다. 이때, 학습 가능한 전체 bias generator network를 $\eta$로 표시하며, $N_P$ 는 base model의 prameter 총 수 이다.

구체적으로, 저자가 설계한 Regional Bias Generator는 두 개의 변환 $F_1 : \mathbb{R}^{D_R} \rightarrow \mathbb{R}^{D_ {O}}$, $F_2 : \mathbb{R}^{D_ {O}} \rightarrow \mathbb{R}^{N_ {P}}$로 구성된 함수 $F_ {\eta}(\cdot)$ 이다. 그리고 이 두 과정을 완전 연결 계층으로 구현하여 Regional Bias Generator를 생성하였다. 이 방법은 미분 가능성과 해석 가능성을 더 잘 보장하였다. 또한, 다양한 ST dynamics를 고려를 할 뿐만 아니라, 한 지역 프로필이 다른 지역과 유사할 때 초기 예측 network가 그들에 대해 비슷한 경향을 갖을 수 있도록 parameter를 조정하였다. 이는 지역 프로필과 ST dynamics 간의 내재된 상관관계가 잘 연결되고 학습되도록 유도하였다.

[3] Model Optimization

모든 task에서 공유된 regularity는 몇 개의 샘플만으로 특정 지역을 적합하게 만드는 데 기여하고, non-shared region-specific ST dynamics는 예측 모델의 신뢰도를 향상시켜서 부정적인 transfer 문제를 완화한다. 이를 위해 저자는 shared generalizable parameter과 variable bias를 사용한 biased initialization meta-learning strategy를 제시하여 region-adaptive prediction을 세밀하게 수행하도록 하였다.

이를 수행하기 위한 알고리즘은 위 그림과 같으며, 자세한 설명은 아래와 같다. 먼저, 각 훈련 task $T_{ri} \in T^{tr}$ 에 대해, 지역 프로필 $e_{ri}$에 따라 특정 base model이 shared parameters $\theta$와 characteristic bias $b_{ri}$로 초기화된다.

$\phi_{ri} \leftarrow \theta + \gamma b_{ri}, \quad b_{ri} = F_{\eta}(e_{ri})$

여기서 $\gamma$는 region-specific knowledge를 공유된 지식에 얼마나 추가할지를 제어하는 개인화된 업데이트 비율이다. 이후, model-agnostic meta-learning (MAML)기반 episode 훈련 과정을 유지하면서, local-update와 global-update의 두 단계가 있다.

local-update 단계 동안, 특정 지역에 대한 로컬 네트워크는 전통적인 신경망 훈련과 유사하게 좋은 로컬 최적점으로 수렴하는 것이 기대한다. 따라서, 각 $T_ {ri} \in T^{tr}$의 support set $D^{sp}_ {ri}$ 에 따라 로컬 학습률 $\alpha$로 예측 손실 $L^{sp}_ {D_ {ri}}$을 최소화하여 local network를 업데이트 한다.

$\phi^{*}_ {ri} \leftarrow \phi_ {ri} - \alpha \nabla_ {\phi_ {ri}} L^{sp}_ {D_ {ri}}(\phi_ {ri})$

global-update 단계 동안, 저자의 목표는 few-shot tasks를 맞출 수 있는 shared generalizable prediction model $\theta^{*}$ 와 프로필과 ST dynamics를 연결하는 효과적인 bias generator $\eta^{*}$를 얻는 것이다.

그래서, local-update 이후 훈련 task $T_ {ri}$의 query set $D^{qr}_ {ri}$ 에 대한 손실의 합을 기반으로 두 매개변수를 업데이트하기 위해 one-step gradient decent를 수행한다.

$\theta^* \leftarrow \theta - \lambda \sum_ {T_ {ri} \in T^{tr}} \nabla_\theta L^{qr}_ {D_ {ri}}(\phi^{*}_ {ri})$ $\eta^{*} \leftarrow \eta - \lambda \sum_ {T_ {ri} \in T^{tr}} \nabla_\eta L^{qr}_ {D_ {ri}}(\phi^{*}_ {ri})$

여기서 $\lambda$는 global-update의 학습률이며, $L^{qr}_ {D_ {ri}}$는 예측 task 에 대한 query set $D_ {ri}^{qr}$의 예측 손실이다.

support-set ($D_ {ri}^{sp}$), query-set ($D_ {ri}^{qr}$) 등의 Meta-learning setting에 대한 설명은 앞 3.2에 나와있으니 함께 참고하길 바란다.

5. Experiment

Experiment setup

Dataset
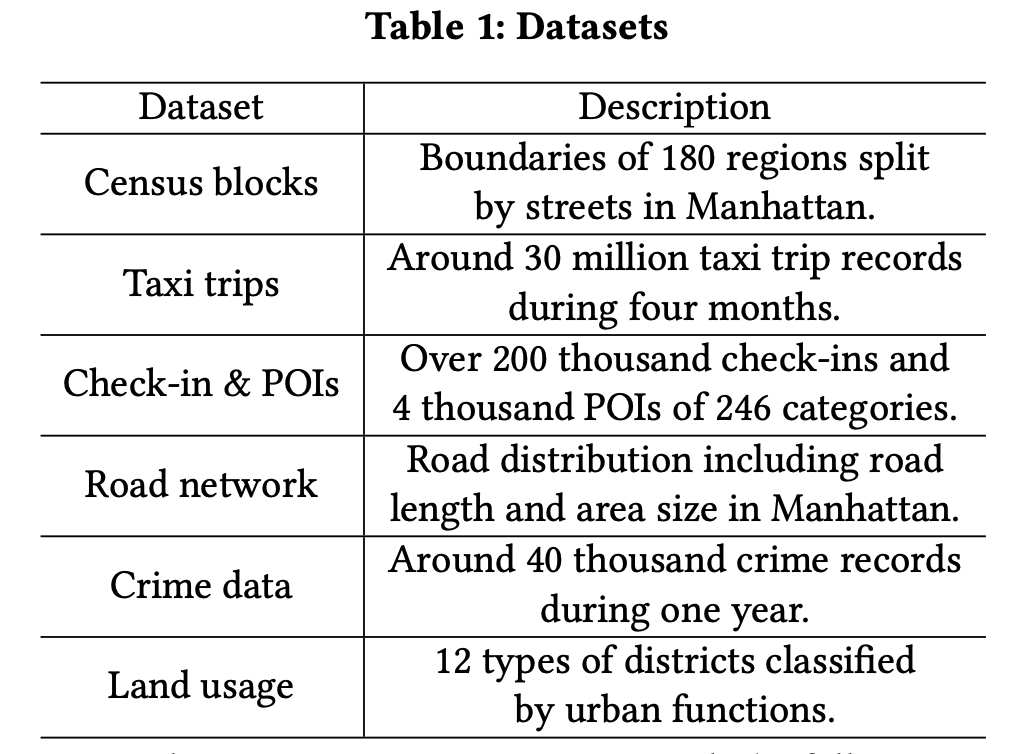
- 위의 테이블에서 보이는 데이터의 설명에서와 같이, 180개 지역에서 발생한 택시 이동 데이터, POI 관심 지점 데이터, 도로 네트워크 데이터를 가지는 뉴욕시 공개 데이터를 활용하였다.
Task
- 저자는 지역의 미래 픽업 및, 하차량을 예측하는 것을 과제로 설정하고 택시 이동 데이터를 사용해서 실험을 수행하였다. 각 지역에 대해서 30분 단위로 volume을 계산하였고, 대략 5760 time slot 중에 80%를 학습 데이터로 나머지 20%를 평가를 위해 사용하였다.
baseline
- 저자는 GAT-GRU 기반의 모델들을 baseline으로 사용하였다. 구체적인 모델로는DCRNN, MAML, ST-MetaNet, MetaPTP가 있다.
- 그리고, MetaRSTP의 임베딩 방식을 평가해보기 위해, MetaRSTP의 임베딩 방식을 node2Vec, MVURE, MGFN, ReMVC의 multi-view region profiling 방식으로 임베딩을 바꿔보았다.
Evaluation Metric
- 저자는 성능 비교를 위해, MAE와 RMSE를 사용하였다.

Result

저자는 먼저, 현 MetaRSTP가 기존 방법들보다 few-shot 시나리오와 common 시나리오에서 좋은지 살폈다.

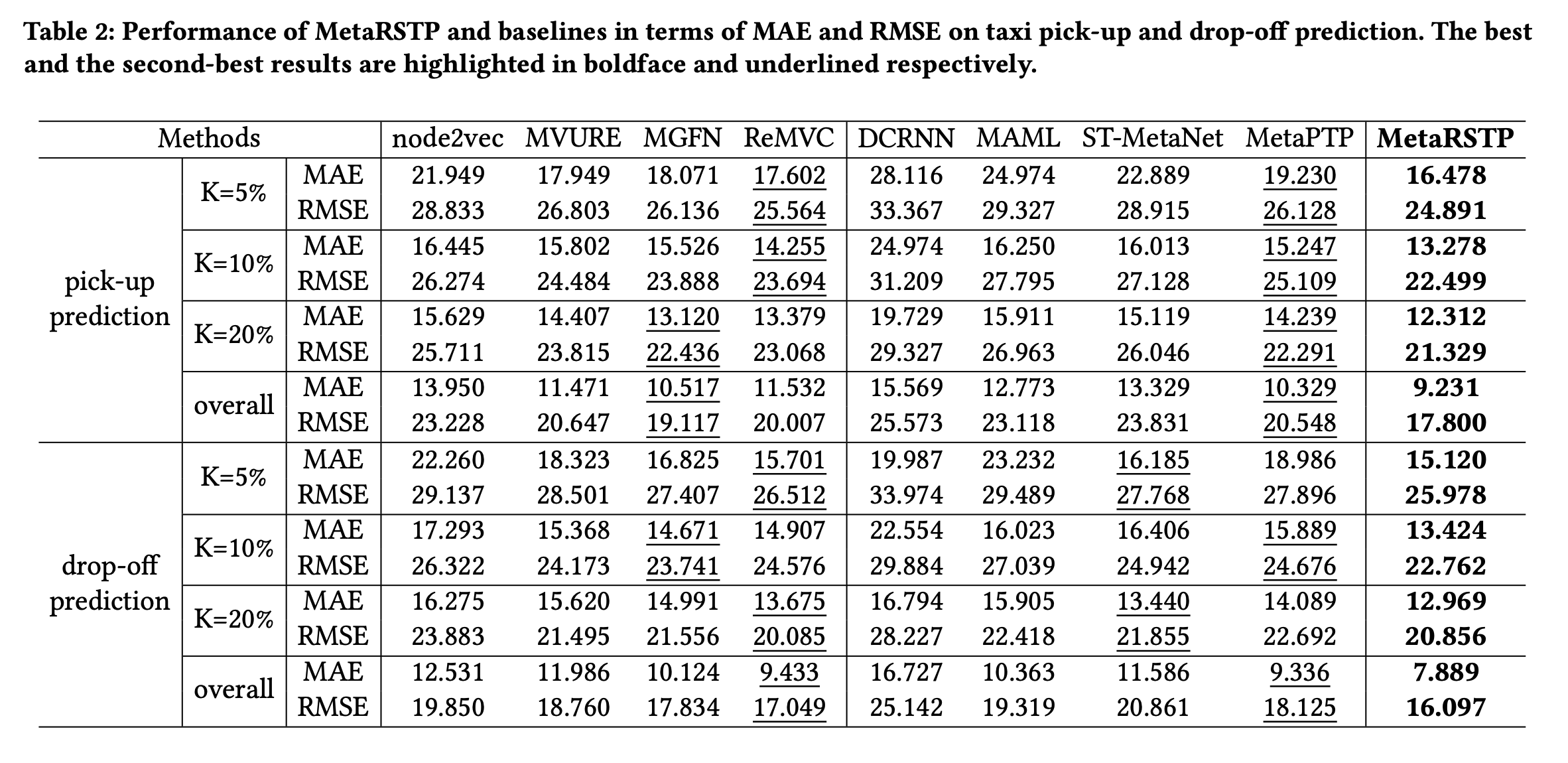
그 결과, 위의 결과에서 보듯 픽업 및 하차량 예측에 대한 성능이 기존의 모든 연구보다 좋다고 나타났다. 저자가 제시한 임베딩 방식이 기존 임베딩 방식보다 좋으며, 모델 구조 또한 더 좋은 성능을 냈다. 특히, K가 훈련 샘플 비율을 나타내는데, 5%,10%,15%의 few-shot scenario에서도 예측을 잘하고 있다는 것을 알 수 있다.

다음으로, 저자는 제안된 방법 중에 어떤 것이 영향을 성능 향상에 영향을 미쳤는지 ablation study를 수행하였다.

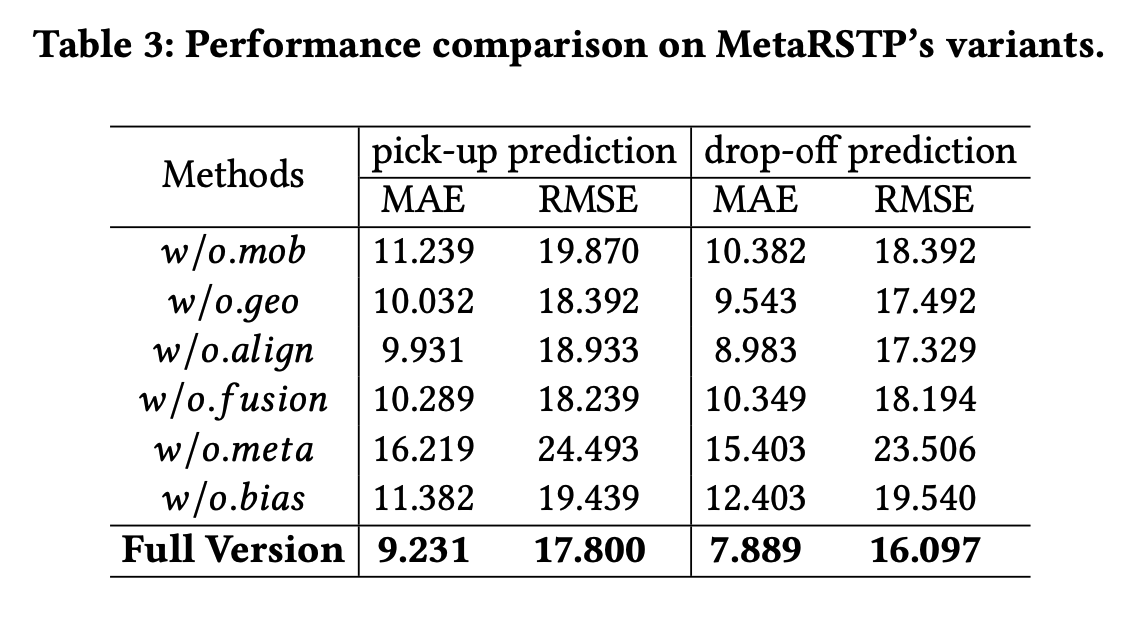
그 결과, 여러 view의 정보를 고려하는 MetaRSTP는 single view 데이터만 고려하는 모델보다 일반적으로 더 나은 성능을 보였다. 또한, fusion 연산과 alignment 연산은 모두 중요하였다. veiw fusion과 semantic alignment을 제거한 변형 모델은 완전한 버전보다 성능이 떨어졌으며, 이는 veiw 간 정보 전파의 중요성을 최대한 활용하고 각 view의 독특한 표현력을 보장하는 데 중요함을 입증하였다. 마지막으로, 메타러닝 프레임워크 없이 기본 모델만 사용하는 경우와 지역 특화 지식 없이 동일한 초기화를 사용하는 MAML 모델은 지역별로 미세 조정에 실패하면서 퇴화하였고, MetaRSTP보다 성능이 떨어졌다. 이는 bias 생성 방법이 각 지역에 대해 신뢰할 수 있는 초기 네트워크를 도출하고 다양한 지역 간 지식을 전달하는데 도움이 됨을 증명하였다.

5. Conclusion

이 논문에서 저자는 MetaRSTP, 적응형 메타러닝 프레임워크를 제안하였다. 이 프레임워크는 strong 지역 프로필을 통해 few-show scenario에서 personalized ST prediction 성능을 향상시키는 것을 목적으로 하였다. 먼저 semantic alignment와 fusion을 통해 지역의 functions을 밝힐 수 있는 포괄적인 multi view 지역 프로필을 학습하였다. 이어서 Regional Bias Generator는 지역 프로필과 ST dynamics 간의 내재된 상관관계를 추가로 모델링하였다. 그 다음으로 biased initialization meta-learning은 지역 전반의 regularity와 지역 특정의 semantics을 사용하므로써 few shot scenario에서 더 나은 region-adaptive prediction을 가능하게 하였다. 마지막으로 실제 세계의 데이터셋에서 실시한 광범위한 실험들은 MetaRSTP의 우수성과 지역 프로필의 유효성을 입증하였다.

소감.

지역간의 근접성과 지역내의 근접성을 활용하여 각자의 특징과 서로의 공통적인 특징을 뽑아 지역 프로필을 추출하는 것을 보며, 단순히 데이터를 사용하는 것이 아니라 관계를 이용하는 것이 중요하다는 것을 깨달았다.
지역간의 근접성으로 co-semantic 관계를 뽑을 수 있다면, 반대로 지역간의 non-co-semantic도 모델에 반영할 수 있었으면 좋겠다고 생각했다. 예를 들면 도시와 시골등의 관계를 활용하는 것등이 있다.