[Recsys 2021] Quality Metrics in Recommender Systems: Do We Calculate Metrics Consistently?
추천시스템은 일반적으로 기업이 이익을 극대화하기위해 사용되고, 이에따라 산업계와 밀접하게 연관되어있다고 생각합니다.
추천시스템만을 다루는 Recsys, 그중 industrial part에서 이러한 논문을 선정한데에는 그만큼 실제 산업에서 추천시스템을 다룰때 믿을만한 평가기준이 중요하다는것을 의미한다고 생각합니다.
저 또한 연구를 진행하면서 가장 중요한 부분중 하나인 평가지표에 대해서는 다른사람들의 구현을 그대로 사용하기도 하는 등, 별다른 관심을 가지지 않고있었어서 이번기회에 추천시스템에 관심있는 학우분들께 다같이 생각해 볼 수 있는 기회가 되었으면 하여 소개하게 되었습니다.
0. ABSTRACT
논문에서 정의하는 오프라인 테스트는 A/B 테스트가 아닌 metric을 사용하는 일반적인 테스트이다.
이러한 오프라인 테스트는 A/B 테스트에 비해 비용이 없다시피하고 일관성을 가질 수 있으나, 실제로 현장에서 사용될 때는 종종 생각과 달리 움직이는 면이 있다.
적절한 metric 이 사용되고 있지 않거나, 같은 metric을 사용한다고 하지만 실제로는 그 계산 방식이 매우 상이한 것도 있다.
저자들은 다양한 추천시스템 프레임워크와 논문들을 살펴보며 이에 대해 논의해보고, 각 metric에 대한 정확한 정의와 세부사항에 대한 합의가 필요함을 이야기 하고자 한다.
1. INTRODUCTION
추천 시스템에서 가장 효과적인 평가방식은 A/B 테스트이다. 다만, 이는 시간적으로나 비용적으로 현실적이지 못한 경우가 많기 때문에, 주로 metric을 사용하는 오프라인 테스트를 사용하게 된다.
테스트는 크게 온라인과 오프라인 두 가지 평가 방법으로 나뉜다. 온라인은 실제 서비스에 적용해 유저의 반응을 살펴보는 방식이다. 오프라인 테스트는 과거에 적용한 알고리즘의 이력(히스토리) 데이터를 이용해 B알고리즘의 성능을 추론한다. 비용이 높다는 단점이 있는 온라인 A/B 테스트의 대안으로 등장했다. 하지만 많은 가정이 필요하고 결과가 실제 결과와 다를 수 있다는 위험(리스크)가 존재한다. [NDC21-오프라인 A/B 테스트 필요성과 적용 사례]
이러한 오프라인 테스트에서 가장 중요한 것 중 하나가 일관성 있고 정확한 metric 인데, 최근 추천시스템에서는 결과의 재현성과 신뢰성에 우려를 나타내는 보고들이 나오고 있다. 이는 추천시스템이 아직 발전하고있고 계속하여 발전하는 영역이기 때문에 보편적으로 적용되는 프로토콜이 없고, 평가를 위해 다양한 metric 들이 산재하기 때문인 것으로 보인다.
저자들은 일반적으로 베이스라인 실험을 위해 사용되는 라이브러리들과 이들 논문들을 대상으로 적절한 metric을 정확한 계산방식에 따라 사용했는지에 대한 리뷰를 다루며, metric 계산방식을 체계화 하여 요약하였다고 이야기 한다.
2. EVALUATION METHODOLOGY
Evaluation 과정에서의 명시적인 선택들은 결과에 영향을 끼치기에 논문을 작성함에 있어 이러한 프로토콜들을 정의하여야 할 필요가 있다. 데이터 셋 선택, 데이터 필터링, 분할 전략(splitting strategy), 순위를 매길 항목 선택(choice of items to rank), metric 및 컷오프 depth가 이러한 프로토콜에 해당되고, 저자들은 이를 모든 실험에서 통일하여 일관성을 갖췄음을 밝힌다.
본 논문에서는 HitRate, Precision, Recall, MRR, MAP, NDCG, RocAuc를 주요한 metric으로 뽑고있다.
앞의 나머지는 depth cut-off 20 (k=20)을 기준으로 하였으며, RocAuc는 training data를 제외하고 사용했다.
저자들은 ‘RePlay’라는 자신들의 library를 포함 Beta RecSys , DaisyRec , RecBole , Elliot , OpenRec , DL RS Evaluation, MS Recommenders, NeuRec , RecSys PyTorch , rs_metrics 을 비교하였다.
데이터셋과 모델로는 Movie-Lens20m 과 EASE를 사용했다(Autoencoder’st 모델, hidden layer 없이 closed form을 가짐-리뷰) 4.5점 미만은 negative, 이상은 positive 처리했다.
Test set으로는 가장 최신의 20%를 가지도록 global timestamp split을 진행, testset 에서만 나타나는 user, item은 제거하였다. 당연하게도 train/test set은 고정하여 진행되었다.
3. EVALUATION
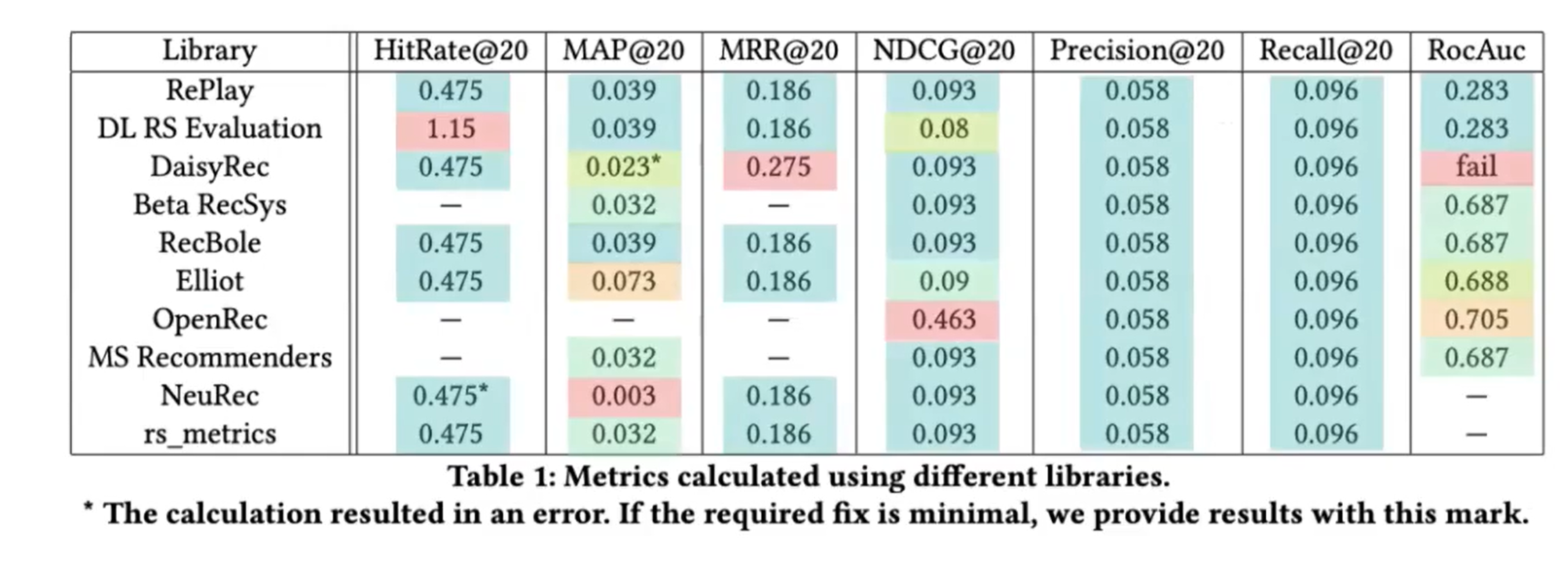 결과는 꽤나 흥미로운데, Precision, recall을 제외한 모든 metric에서 라이브러리에 따라 다양한 결과가 발생한다.
결과는 꽤나 흥미로운데, Precision, recall을 제외한 모든 metric에서 라이브러리에 따라 다양한 결과가 발생한다.
Notations
- $u$ is a user identificator
- $i$ is an item identificator
- $rec_k(u)$ is a recommendation list for user $u$ containing top-k recommended items
- $rel(u)$ is a list of relevant items for user u from the test set
- $rank(u,i)$ is a position of item $i$ in recommendation list $rec_k(u)$
- $I[·]$ is an indicator function
- 별다른 표현이 없는 경우 모든 metric은 단일 user에 대해 평가 후 전체 유저에 대해 평균을 낸다.
3.1 Precision and Recall
믿음의 precision and recall, 이걸 자의적으로 해석하는 경우는 없다.
- Precision
추천한 k개 item 중에 hit한 item의 비율$ \text { Precision@k(u)=} \frac{\left|\operatorname{rel}(u) \cap \operatorname{rec}_{k}(u)\right|}{k} $
- Recall
relevant item 중에 hit 한 item의 비율$ \text { Recall@k(u)=} \frac{\left|\operatorname{rel}(u) \cap \operatorname{rec}_{k}(u)\right|}{|\operatorname{rel}(u)|} $
3.2 HitRate
(Single user) k개의 추천 목록 내에서 적어도 하나가 relevant 이면 1, 아니면 0
→ 전체 user 에 대해 hit 한 비율 : HitRate@k(u)
$ \text { HitRate@k(u)=I[|rel(u)}\left. \cap \operatorname{rec}_{k}(u) \mid>0\right] $
상식적으로 Hit rate는 1이하여야 하나 DL RS Evaluation 에서는 1이 넘는 경우가 발생, 해당 문제는 올바르게 예측한 항목의 평균수(precision*k)를 Hitrate라 칭한것으로 나타남
3.3 MRR(Mean Reciprocal Rank)
(Single user) k개의 추천 목록 내에 첫번째로 relevant 한 item position의 역수
→ 전체 user에 대해 해당 inverse position 의 평균 : MRR@k(u)
$ M R R @ k(u)=\frac{1}{\min _{i \in \operatorname{rel}(u) \cap \operatorname{rec}(u)} \operatorname{rank}(u, i)} $
DaisyRec 의 경우 첫번째 relevant item 의 inverse position 이 아닌, 전체 relevant item 들의 inverse position의 합을 계산했음. 이때 MRR은 1이 넘을 수도 있다.
3.4 MAP(Mean Average Precision)
(Single User의 AP)
AP@k(u) : user u에 대한 Precision 의 평균
→모든 user 에 대한 AP의 평균 : MAP
$ A P @ k(u)=\frac{1}{x} \sum_{i \in \operatorname{rec}_{k}(u)} \mathbb{I}[i \in \operatorname{rel}(u)] \operatorname{Precision@rank}(u, i)(u) $
MAP 에서 ‘M’ 에 해당하는 mean term 은 일반적으로 이견이 없다. 문제는 ’A’에 해당하는 averaging term $x$ 의 정의가 모호하다는 것, 일반적으로는 해당 세개 중 하나의 의미가 사용된다.
- $x=k$ : 추천 목록 item의 수(length of recommendation list)
- $x = r=\vert rel(u)\vert $ : user 의 relevant item의 수
- $x = min(k,r)$
MAP 는 모든 metric 중 가장 일관성 없는 값을 보였음(5개)
-
AP는 원래 precision-recall curve 에서 area를 의미하기 때문에, recall 에 해당하는 relevant item 수를 를 가져가는게 합당해보이다. 두번째 케이스인 $x=r$ 이 이에 해당한다. Beta Recsys, MS Recommenders, rs_metrics. 가 이런 정의를 따른다.
→ 단 r > k 라면 AP는 절대 1에 도달 할 수 없음.
- DaisyRec 은 첫번째 케이스인 x=k를 사용한다. → 단 r < k 라면 더이상 개선 할 수 없음에도 AP는 1을 달성할 수 없음.
-
위 두가지 케이스 때문에 $x = min(k,r)$ 을 사용하는 경우가 있다. RecBole, RePlay , DL RS 는 이러한 이유로 해당 정의를 사용한다.
- 위 세가지를 제외하고도 다른 해석을 적용하는 경우가 있었다. 대부분 구현 실수로 보인다.
- Eliot의 경우 documentation 에서는 $x = min(k,r)$을 사용한다고 적어놓았지만, 실제로는 $x=k$를 사용하였으며, Indicator function을 빼먹어 추천대상이 아닌 아이템에 대해서도 precision 을 계산하였다.
- NeuRec 의 경우 역시 $x = min(k,r)$ 를 사용한다고 적혀있지만, sum 과정에서 변수명 꼬임과 같은 오류로 누적이 제대로 이뤄지지 않아, 이상한 값을 내놓았다.(다른 케이스 대비 1/10 수준)
3.4 NDCG(Normalized Discounted Cumulative Gain)
추천결과의 상위항목에 보다 높은 가중치를 부여하기 위해 사용, 임의의 relevance value인 rating(u,i)를 가중치로 부여.
DCG(Discounted Cumulative Gain)의 이상치인 IDCG(Ideal DCG)와 DCG의 비로 NDCG값이 계산, 이때 Idial 한 값은 rating(u,i)으로 정렬되었을때의 DCG값을 의미
$ N D C G @ k(u)=\frac{D C G @ k(u)}{I D C G @ k(u)} $
DCG-weighted version
$ D C G @ k(u)=\sum_{i \in r e c_{k}(u)} \frac{2^{\text {rating }(u, i)}-1}{\log _{2}(\operatorname{rank}(u, i)+1)} $
DCG-Binary version
$ D C G @ k(u)=\sum_{i \in r e c_{k}(u)} \frac{\mathbb{I}[i \in \operatorname{rel}(u)]}{\log _{2}(\operatorname{rank}(u, i)+1)} $
DCG-??(논문에선 언급하지 않음)
국내 블로그에서는 rating이 정해져 있고, 분자에서 이를 모두 더하는 방식을 많이 소개한다.
$ D C G @ k(u)=\sum_{i \in r e c_{k}(u)} \frac{\text {rating }(u, i)}{\log _{2}(\operatorname{rank}(u, i)+1)} $
라이브러리들은 weighted version 과 binary version 중 하나를 선택하는데
- Beta RecSys, RecBole, RePlay, DaisyRec, MS Recommenders, NeuRec, rs_metrics 에서는 Binary version을 사용.
- OpenRec 에서는 Binary version 을 사용한다고 되어있으나 normalization term 을 빼먹었다. 즉 NDCG 가 아닌 DCG 값을 출력.
- DL RS Evaluation ,Elliot 에서는 weight version을 사용하고 relevance value를 입력하도록 함, 단 Eliot 에서는 $log_2$ 가 아닌 자연로그 사용.
3.6 RocAuc(Reciever Operating Characteristic Area Under Curve)
- (참고)ROC 와 precision-recall은 다르다..
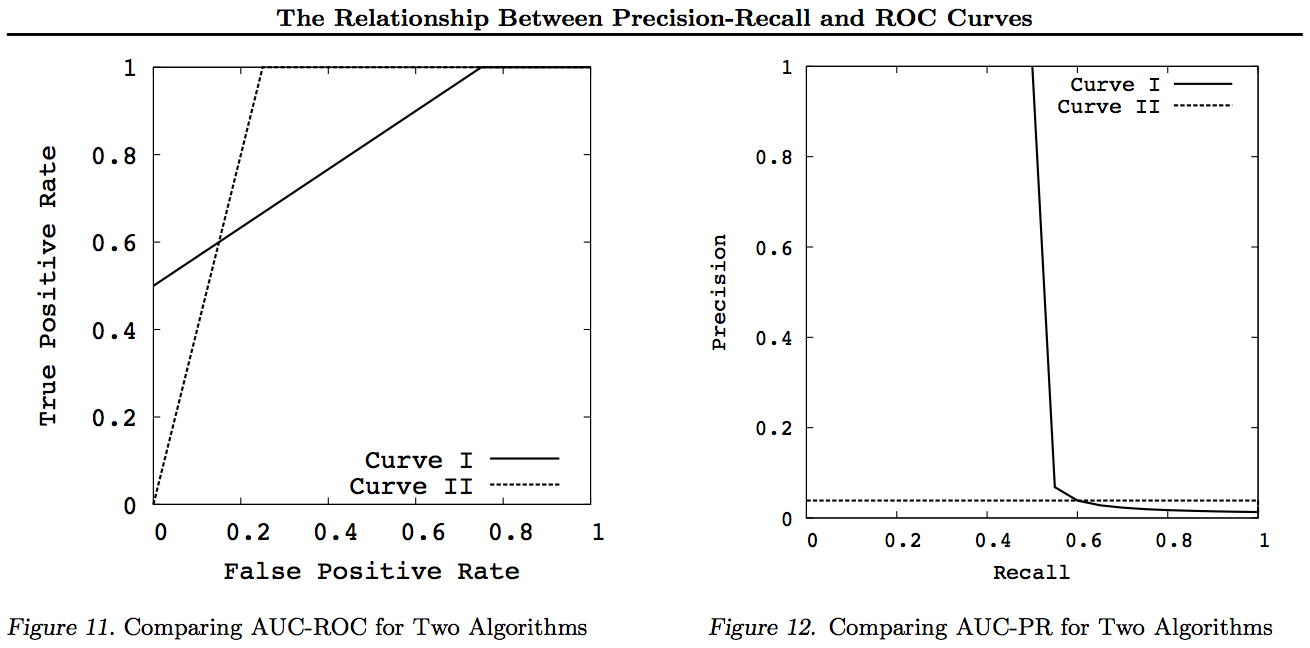 ROC vs precision-and-recall curves
ROC vs precision-and-recall curves
RocAuc는 굉장히 애매하다. 일반적으로 classification 에서 많이 사용되는데(1/0 값을 가지는 이진 결과), 아직 추천시스템에서 어떻게 사용할것인지에 대해 명확히 정해진바가 없음.
그래서 ROC를 왜 쓰게 되었나? ← BPR(Bayesian Personalized Ranking from Implicit Feedback)의 영향으로 보인다.
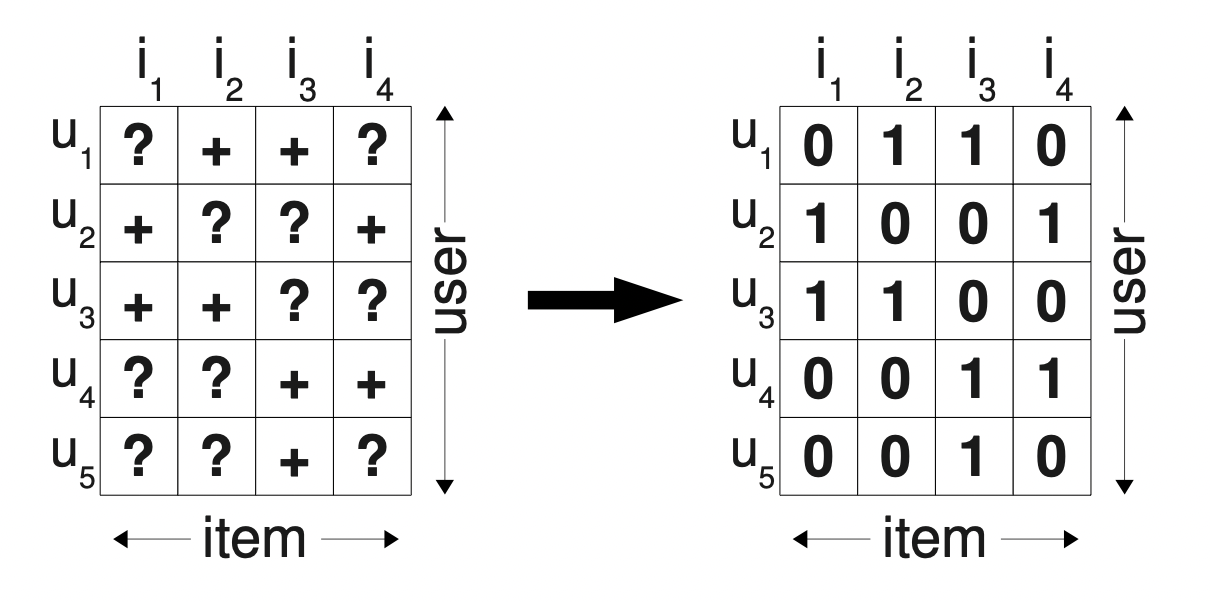
Bayesian Personalized Ranking from Implicit Feedback
1,0의 binary implicit feed을 다룰때 BPR은 사용자의 선호도를 두 아이템 간의 pairwise-ranking 문제로 formulation 함으로써 각 사용자 $u$의 personalized ranking function을 추정
→ User-item 선호를 구분하는 classifier 문제로 생각할 수 있다.
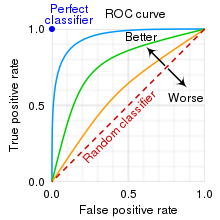
→ 임의의 positive와 negative sample이 주어졌을 때, negative sample보다 positive sample을 더 높은 순위(더 높은 positive 확률)로 평가할 확률을 의미한다.
쉽게말하면 유저에게 item 들이 임의의 rating 을 가지고 있을때 이를 정렬(rating에 따른 ranking)하여 반갈하는 classification 하는 문제로 볼 수 있다는 것
문제는 단순한 생각으로 T/F를 무작위로 찍는 classifier는 RocAuc에서 0.5를 얻겠지만, 무작위로 추천하는 추천시스템에서는 0.5를 얻을리가 없다는 것, 따라서 classifier 와 같은 단순한 생각은 추천시스템에서 곧바로 적용시키기 힘들다.
이러한 상황에서 두가지 핵심적인 결정이 필요한데
- 전체 item 들을 대상으로 생각할 것인지, k 개의 item을 대상으로 할 것인지
- 전체 user 에 대한 계산을 한번에 할 것인지, 아님 개인의 AUC를 구한 뒤 averaging 할 것인지
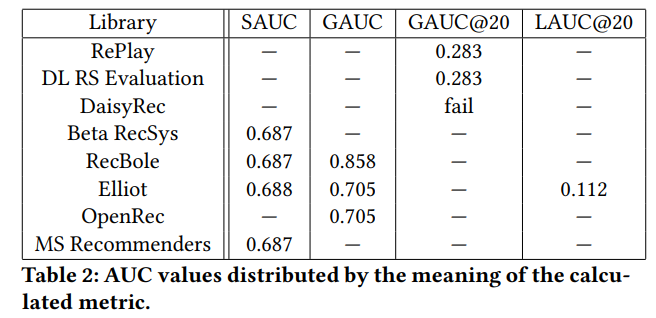
SAUC(Stacked AUC)
가장 simple 하게 생각한다. 전체 item 들에 대해 full ranking 을 부여하고 이를 classification 문제와 같이 다루는 것 Beta RecSys, RecBole ,MS Recommenders
GAUC(Group AUC)
SAUC 에서 서로다른 사용자의 추천이 다른것에 문제 제기, 각 user 의 ROC 커브에서 AUC를 계산 한 후, 이를 averaging. OpenRec, DL RS Evaluation, Elliot, RePlay, RecBole
GAUC@k
전체 ranking 이 아닌 k 개의 ranking 만 고려한다, Replay, DL RS Evaluation, DaisyRec
4. Paper Analysis
위에서 살펴보았듯, 몇몇 metric 들은 잘못해석될 여지가 있고 다양한 베리에이션과 그에 따른 해석이 존재한다. 문제는 어떤 metric 을 사용했는지 정확히 적어두기라도 했으면 모르겠는데, 그렇지 않은 경우가 많다는 것이다. 논문에서도 이러한 현상은 비슷하게 나타는데, 저자들은 이를 확인하기 위해 몇몇 베이스라인으로 주로 사용되는 논문들에서는 이를 어떻게 다루는지 살펴보았다.
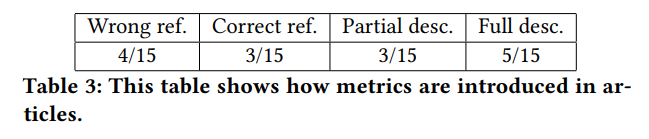 자신들이 사용한 metric 에대해 정확히 기술한 논문은 5/15, 정확히 기술한 레퍼런스를 단 논문은 3/15, 잘못된 레퍼런스를 달았더나 정확히 어떤 metric 을 사용했는지 알 수 없게 기술한 경우는 7/15 거의 절반에 가까운 상황이었다.
자신들이 사용한 metric 에대해 정확히 기술한 논문은 5/15, 정확히 기술한 레퍼런스를 단 논문은 3/15, 잘못된 레퍼런스를 달았더나 정확히 어떤 metric 을 사용했는지 알 수 없게 기술한 경우는 7/15 거의 절반에 가까운 상황이었다.
- Recsys의 큰 획을 그은것으로 여겨지고 그만큼 많이 인용되는 NCF(Neural Collaborative Filtering) 의 경우
“the HR intuitively measures whether the test item is present on the top-10 list, and the NDCG accounts for the position of the hit by assigning higher scores to hits at top ranks.” 와 같이 명확하지 않은 설명을 적어놓았다. 물론 HR 과 NDCG에 대해 정확히 적어놓은 TriRank: Review-aware Explainable Recommendation by Modeling Aspects 를 참조했지만 두 논문의 Hit rate는 같은 의미였던 반면 NDCG에서는 모순된 결과를 보였다.
-
MultiVAE(Variational Autoencoders for Collaborative Filtering) 에서는 recall에서 위에서 설명한 것들과는 달리 또다른 정의를 사용한다.
AP 에서처럼 rel(u) 대신 min(r,k)를 사용)
- CDL(Collaborative Deep Learning for Recommender Systems) 에서는
“Another evaluation metric is the mean average precision (mAP)” 로 설명을 끝내고 만다. 이는 MAP 가 가장 variation 이 컸던만큼, 결과해석을 어렵게 만드는 부분이다.
5. CONCLUSION
저자들은 라이브러리와 논문들에서 다양한 metric 들이 어떤식으로 차이를 보이는지 살펴보았고, 각 metric 들이 표준화 되지 않아 다양하게 해석될 가능성이 있음을 설명한다.
일반적으로 단순한 metric 일 수록 의견차가 없음(precision, recall등)이 나타났고, 복잡한 metric 일 수록 다양한 해석이 존재하였다. 이에대해 recommenation system 커뮤니티에서 표준화된 합의가 필요함을 밝히며 논문을 마친다.
6. OPINION
특히 baseline등을 구현할 때 별 생각없이 사용해오던 구현체 들이 많은데, 이번 논문을 읽으며 좀 더 주의하고 한번 더 코드를 살펴봐야겠다는 경각심을 갖게 되었습니다.
저자들은 future work로 별다른 내용을 담진 않았지만, 실제 산업에서 A/B 테스트 대비 어떤 metric이 비슷한 결과를 보이는지에 대한 연구를 진행하면 좋겠다 라는 생각이 들었습니다.
특히 rating prediction 문제에서는 rmse를 평가지표로 많이 활용하는데, 이러한 결과가 실제 구매/클릭 전환에 얼마나 기여하는지에 대한 궁금증이 있어왔습니다. 공개된 데이터셋으로는 아마 쉽지 않겠지만, 기회가 닿는다면 이러한 연구를 진행해 보고 싶습니다.