Title

MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems

1. Problem Definition

Graph Neural Networks (GNNs)은 논문 작성 당시 state-of-the-art collaborative filtering (CF) solution으로 부상하였다. CF의 근본적인 challenge는 implicit feedback에서 negative signal을 추출하는 것이지만 GNN 기반 CF 모델에서의 negative sampling에 대한 연구는 많이 부족하다.
추천시스템에서 negative sampling이란 사용자에게 관심을 끌만한 아이템을 추천하기 위해 사용되는 기술로 사용자가 관심을 가질 가능성이 낮은 아이템을 선택하여 negative example로 사용하는 것을 말한다.
보통 negative sampling은 다음과 같은 단계로 이루어진다.

사용자의 이전 행동 기록에서 positive feedback(예: 구매, 평가 등)을 수집한다. 이를 기반으로 사용자의 관심사를 파악한다.
사용자의 관심사를 파악한 후 해당 사용자에 대해 positive feedback이 아닌 아이템들 중에서 몇 개를 무작위로 선택한다. 이러한 아이템은 negative sample로 간주된다.

Negative sampling을 통해 모델의 학습 효율성을 높일 수 있으며, 사용자에게 다양한 아이템을 추천함으로써 다양성 또한 높일 수 있다.

2. Motivation

일반적으로 negative sampling에는 uniform distribution이 사용된다. negative samples의 quality를 향상시키기 위해 유익한 negative sample의 우선순위를 정하기 위한 새로운 sampling distribution을 설계하려는 연구들이 있었다. GNN에서는 Negative Sampling을 개선하기 위해 다음과 같은 연구가 진행되었다.

PinSage: PageRank 점수를 기반으로 negative sampling
MCNS: structural correlation을 염두해 두고 positive와 negative sampling의 분포를 재설계

하지만 GNN에서의 이러한 시도는 GNN의 embedding space에서의 고유한 neighborhood aggregation 과정을 무시하고 불연속 graph space에서의 negative sampling을 개선하는 데에만 초점을 맞춘다.
MixGCF는 데이터에서 실제 negative sample을 직접 sampling하는 대신 hard negative sample을 합성한다. 그리고 기존 GNN 기반 추천 모델을 연결하여 사용할 수 있는 positive mixing과 hop mixing 전략을 제시하였다.

3. Method

MixGCF는 GNN 기반 추천에서 negative sampling을 위한 일반적인 알고리즘으로 LightGCN 및 NGCF와 같은 기존 GNN 기반 추천 알고리즘에 연결하여 사용할 수 있다. data의 실제 item을 negative item으로 샘플링하는 대신 GNN 기반 추천 모델을 학습하기 위해 그래프 구조를 기반으로 informative하고 fake한 negative item(hard negative item)을 합성할 것을 제안한다. 특히 서로 다른 local graph의 정보를 mixing하여 negative sample을 합성하는 positive mixing 및 hop mixing 전략을 도입하였다.

MixGCF의 흐름은 아래 그림과 같다.

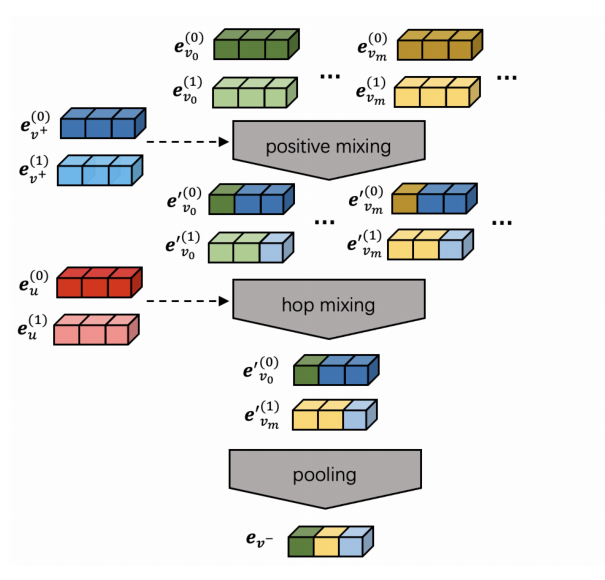
positive mixing에서 positive sample의 정보를 negative sample에 주입하여 hard negative candidates를 만드는 interpolation mixing 방법을 활용한다.
hop mixing에서 먼저 hard negative selection 전략을 사용하여 위에서 생성된 각 hard negative candidates에서 고유한 정보를 추출한 다음
pooling 작업을 하여 추출된 다양한 정보를 결합, fake지만 informative한 negative item들을 생성한다.

3.1 Positive Mixing

$L$-layer GNN에서 각 item $v$에 대해 $L+1$ 개의 embedding을 가질 수 있으며, 각 $e_v^{(l)}$은 l layer $(0 \le l \le L)$로 aggregate 되는 embedding을 의미한다. negative $v_i^-$를 그것의 embedding인 $e_{v^-}$과 함께 fake로 만들기 위해 $M$개의 negative item을 선택하여 $M$이 일반적으로 데이터의 아이템 수보다 훨씬 작은 candidate set M 을 만든다. 이러한 $M$개 negative 아이템은 $M * (L + 1)$ size의 cadidate negative embedding set $\varepsilon = \lbrace{e_{v_m}^{(l)}}\rbrace$ 를 형성할 수 있다.

Positive mixing은 mixup의 영향을 받아 $\varepsilon$에 속한 negative embedding에 positive information $e_{v^+}$을 주입한다. mixup은 interpolation 기반 data augmentation 방법으로 model이 training data 간에 선형적인 output을 갖도록 해준다. 각 candidate negative embedding ${e_{v_m}^{(l)}} \in \varepsilon$에 대하여 positive mixing 작업은 다음 식과 같이 이루어진다.

$\mathbf{e}_ {v_ m}^{(l)}=\alpha^{(l)} \mathbf{e}_ {v^{+}}^{(l)}+\left(1-\alpha^{(l)}\right) \mathbf{e}_ {v_ m}^{(l)}, \alpha^{(l)} \in(0,1)$

여기서 $\alpha^{(l)}$은 각 홉 $l$에 대해 균일하게 샘플링되는 mixing coefficient 이다. 이 때 mixup의 mixing coefficient는 model의 generalization 능력에 큰 영향을 미치는 beta distribution Beta $(\beta, \beta)$에서 sampling된다. 그 영향을 decoupling하기 위해 해당 모델에서의 postive mixing에서의 mixing coefficient $\alpha^{(l)}$는 (0,1) 범위에서 균일하게 sampling된다.

$\varepsilon^\prime$을 candidate negatives set M에 대해 강화된 embedding이라고 정의한다. Positive mixing은 다음과 같은 방법들을 활용하여 negative를 강화시킨다.

negative sample에 positive 정보를 주입하여 decision boundary를 더 잘 활용하도록 optimization 알고리즘을 수행하게 하는 데 도움을 준다.
random mixing coefficient를 사용하여 확률적 불확실성을 도입한다.

3.2 Hop Mixing

hop mixing은 positive mixing에 의해 강화된 candidate negative items embedding $\varepsilon^{\prime} = \lbrace{e_{v_m}^{\prime(l)}}\rbrace$ 를 가지고 합성 negative item $v^-$ 과 그것의 embedding $e_{v^-}$를 만드는 방법이다.

hop mixing의 main idea는 GNN의 layer 기반 계층적 aggregation process를 활용하는 것이다. 각 layer $l(0 \le l \le L)$로부터 M에 속한 모든 candidate negative item에 대한 $l$번째 layer embedding이 포함된 $\varepsilon^{\prime(l)}$에서 하나의 candidate negative embedding $e_{v_x}^{\prime(l)}(1 \le x \le M)$을 뽑는다. 여기서 $x$는 negative sample set에서의 index를 의미한다.

만약 $L = 2$라면 $e_{v_a}^{\prime(0)}, e_{v_b}^{\prime(1)},e_{v_c}^{\prime(2)}$를 $\varepsilon^{\prime}$에서 뽑을 수 있고 $a, b, c$는 반드시 별개일 필요는 없다. hop mixing은 각 layer에서 선택한 모든 $(L+1)$개의 embedding을 결합하여 fake negative $v^-$에 대한 representation $e_{v^-}$를 생성한다. representation은 pooling 작업을 통해 모든 candidate embedding을 융합함으로써 합성된다:
$e_{v^-} = f_{pool} \left(e_{v_x}^{\prime(0)}, \cdots ,e_{v_y}^{\prime(L)}\right)$

이 때 $e_{v_x}^{\prime(l)}$는 layer $l$ 에서 뽑힌 $v_x$ 의 $l$ 번째 layer embedding이고 $f_{pool}(\cdot)$은 GNN 기반 추천 모델에서 쓰이는 pooling과 동일한 연산을 적용한다.

hop mixing에 대한 중요한 질문은 어떻게 각 layer $l$의 $\varepsilon^{\prime^{(l)}}$에서 candidate embedding ${e}_{v_x}^{\prime(l)}(1 \le x \le M)$를 잘 뽑는가이다. 논문에서 negative sampling에 대해 제안하는 방법은 추정된 positive distribution에 따라 negative sample을 선택하는 것이다. 내적 score를 통해 positive distribution을 근사화하고 가장 높은 점수를 가진 candidate sample을 선택한다. 이 전략을 hard negative select strategy 라고도 한다.

$l$번째 layer에서의 hard selection strategy는 다음과 같이 구현된다:

$\mathbf{e}_ {v_x}^{\prime(l)}=\underset{\mathbf{e}_ {v_m}^{\prime(l)} \in \mathcal{E}^{(l)}}{\arg \max } f_ {\mathrm{Q}}(u, l) \cdot \mathbf{e}_ {v_m}^{\prime(l)}$

여기서 $\cdot$은 내적 연산이고, $f_Q(u, l)$은 $l$번째 hop에 대한 target user $u$의 embedding을 반환하는 query mapping이다. 위 식의 query는 추천에 사용되는 GNN의 pooling module에 따라 다르다. GNN 기반 추천 모델에서 target user embedding $e_u$와 합성된 negative embedding $e_{v^-}$ 사이의 내적을 구하는 방법은 2가지가 있다

Sum based pooling: $\mathbf e_u\cdot\mathbf e_{v^{-}} = \displaystyle\sum_{l=0}^{L} \lambda_l \mathbf e_u \cdot \mathbf e_{v^{-}}^{(l)}$
Concat based pooling: $\mathbf e_u \cdot \mathbf e_{v^{-}} = \displaystyle\sum_{l=0}^{L} \mathbf e_u^{(l)} \cdot \mathbf e_{v^{-}}^{(l)}$

GNN 기반 추천 모델에서 사용되는 pooling 과 일치하는 selection process를 만들기 위해 위의 식의 $f_{\mathrm{Q}}(u, l)$을 sum based pooling은 $e_u$, concat based pooling은 $e_u^{(l)}$로 정의한다.

3.3 Optimization with MixGCF

MixGCF에서도 다른 gnn 기반 추천 모델의 parameter를 최적화하기 위한 BPRloss를 사용할 수 있다. MixGCF에서의 BPRloss는 다음과 같이 업데이트 될 수 있다:

$\mathcal{L}_ {\mathrm{BPR}}=\sum_ {\substack{\left(u, v^{+}\right) \in O^{+} \mathbf{e}_ {v^{-}} \sim f_ {\mathrm{MixGCF}}\left(u, v^{+}\right)}} \ln \sigma\left(\mathbf{e}_ u \cdot \mathbf{e}_ {v^{-}}-\mathbf{e}_ u \cdot \mathbf{e}_ {v^{+}}\right)$

$\sigma(\cdot)$은 sigmoid function이고, $O^+$는 positive feedback set를 의미한다. 그리고 $e_ {v^{-} \sim f_ {MixGCF\left(u, v^{+}\right)}}$ 는 instance embedding $e_{v^-}$는 제안된 MixGCF 방법으로 합성된다는 것을 의미한다.

위 전체 학습 과정을 알고리즘으로 나타내면 아래와 같다.

4. Experiment

Experiment setup

Dataset
- Alibaba
- Yelp2018
- Amazon
Recommender
- LightGCN
- NGCF
- PinSage
baseline(Negative Sampling)
- static(RNS)
- hard negative(DNS)
- GAN-based(IRGAN and AdvIR)
- graph-based(MCNS)
Evaluation Metric
- Recall@20
- NDCG@20

Result

Performance Comparison

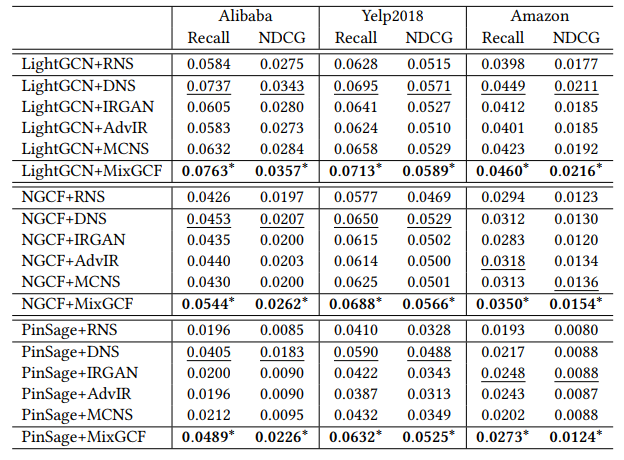
baseline 중 결과가 best인 것은 밑줄, 그리고 MixGCF는 별표로 표시하였다.

LightGCN은 NGCF와 PinSage에 비해 세가지 데이터 모두에서 높은 성능을 보인다. nonlinearity와 weight matrix가 collaborative filtering에 useless함을 확인할 수 있다.
MixGCF는 모든 데이터셋에서 가장 좋은 성능을 보인다. 그 이유는 다음과 같다고 주장한다.
- hop mixing을 통해 negative sample을 생성하여 추천 모델의 generalization 성능을 개선하였다.
- 여러 instance의 서로 다른 information을 통합하여 합성된 hard negative는 추천 모델에 informative한 gradient를 제공한다.
NGCF와 PinSage는 LightGCN에 비해 MixGCF를 사용했을 때 더 큰 성능 향상을 보였다. 그 이유는 다음과 같다.
- burdensome design은 큰 파라미터 공간을 제공하여, NGCF와 PinSage는 informative한 negative로부터 더 많은 이점을 얻는다.
- LightGCN은 positive와 easy negative item을 잘 구별한다.
DNS는 대부분의 경우에서 baseline 중 가장 좋은 성능을 보인다. 이를 통해 hard negative를 선택하는 것이 model에게 의미 있는 gradient를 제공한다는 것을 알 수 있다.

Impact of Presence of Positive Mixing

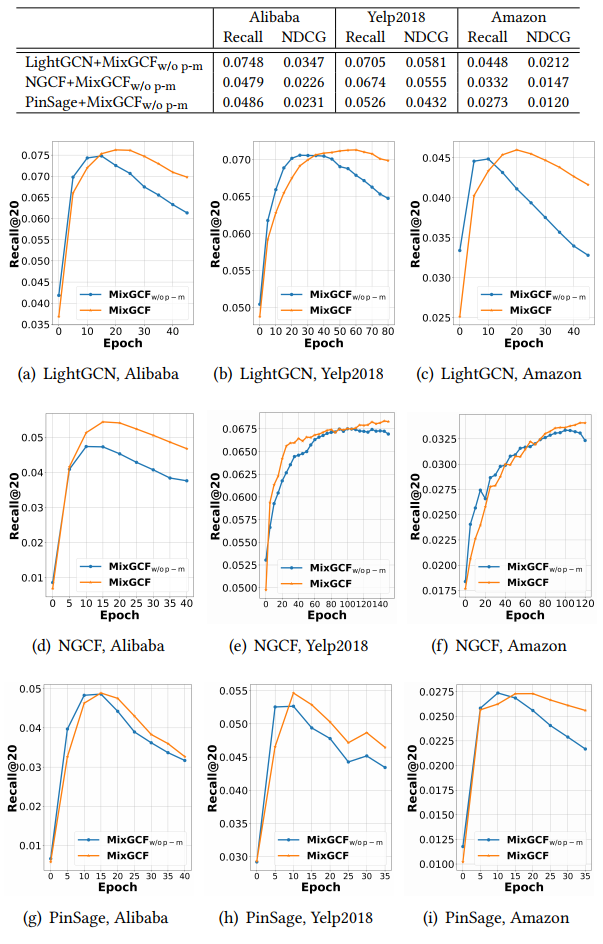
MixGCF$_{w/o \; p-m}$는 positive mixing이 제거된 MixGCF를 의미한다.

위의 (a)부터 (i) 시각화 결과를 통해 대부분의 경우에서 positive mixing을 제거했을 때 성능이 하락하는 것을 볼 수 있다. 이를 통해 positive mixing의 필요성을 알 수 있다.
positive mixing이 제거되어도 MixGCF는 여전히 대부분의 경우에서 DNS에 비해 성능이 높고, 이를 통해 GNN 기반 추천 모델에서 hop-wise sampling이 instance-wise sampling보다 효과적임을 보여 준다.
MixGCF$_{w/o \; p-m}$의 경우 성능이 초기 단계에서 급증하지만 빠르게 최고점에 도달하고 하락하는 것을 볼 수 있다. 반면 MixGCF는 positive mixing의 이점 덕분에 overfitting에 견고해진다.

Impact of Neighbor Range

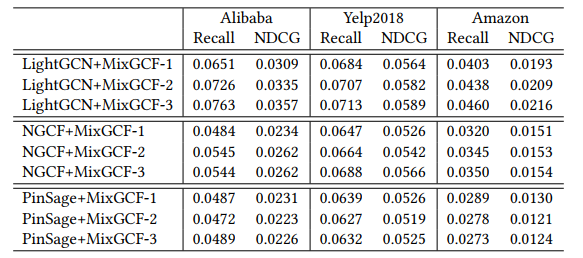
Neighbor range, 즉 layer 개수를 바꾸어 가며 실험을 진행하였다. $L$은 $\lbrace 1, 2, 3\rbrace$ 값을 사용하였다.

layer 수를 늘리면 대부분의 경우 추천 모델의 성능을 향상시킬 수 있다. 더 큰 범위의 neighbor를 고려하면 더 많은 negative item이 negative를 합성할 때 포함될 수 있다.
PinSage에서는 MixGCF-1이 MixGCF-2나 MixGCF-3와 비슷하거나 더 높은 성능을 보인다는 것을 알 수 있다. layer가 많으면 PinSage는 over-smoothing 될 위험이 있기 때문이다.

Impact of Candidate Set

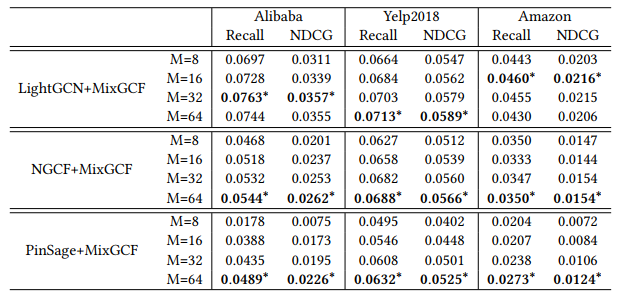
candidate set M의 size를 바꾸어 가며 실험을 진행하였다. $M$은 $\lbrace 8, 16, 32, 64\rbrace$ 값을 사용하였다. 각 데이터 및 모델 별 best result는 별표로 표시하였다.

candidate set의 크기를 늘리면 대부분의 경우 추천 모델의 성능이 향상된다. NGCF의 경우 3 dataset 모두에서 가장 높은 성능을 보인다.
Amazon dataset의 경우 다른 dataset에 비해 M이 증가할 때 성능이 향상되지 않는다. dataset의 scale과 distribution이 다르기 때문이다.

Impact of Distribution of Positive Mixing

random coefficient $\alpha^{(l)}$의 경우 positive mixing에서 핵심이기 때문에, LightGCN에서 random coefficient의 distribution을 바꾸어 가며 실험을 진행하였다. 사용된 분포는 다음과 같다

beta distribution: Beta $(\beta, \beta)$, $\beta$ in range $\lbrace 0.2, 0.4 \rbrace$
gaussian distribution: Gaus $(\mu, \sigma)$, $\mu = 0.5, \sigma = 0.1$
uniform distribution: Uni $(0, \alpha)$, $\alpha = 0.5, 1$

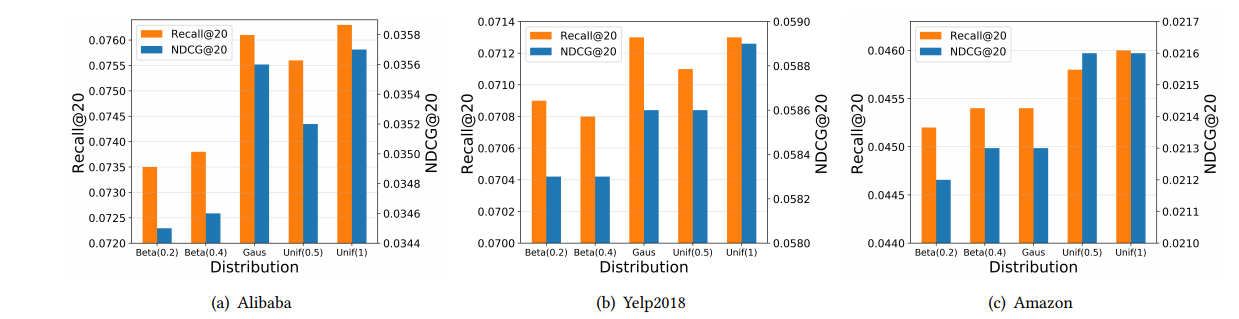
positive mixing의 원래 설정인 Uni(0, 1)의 경우 모든 경우에서 best performance를 보인다. Uni(0, 1)이 Uni(0, 0.5)보다 더 높은 성능을 보이는게 가능한 이유는 random coefficient의 범위를 제한하면 model parameter의 search space가 줄어들기 때문이다.
beta distribution의 경우 모든 3개 dataset에서 좋지 못한 성능을 보인다. 그 이유는 mixup에서 hyperparameter $\beta$의 정교한 선택이 요구되기 때문이다.

위와 같은 이유로 $\alpha^{(l)}$을 sampling할 때 Uniform (0,1) distribution을 사용한다.

5. Conclusion

이 논문은 GNN 기반 추천 모델의 negative sample quality 향상을 목표로 연구를 진행하였다. simple하고 non-parametric한 방법인 MixGCF는 기존 negative item을 sampling 하는 대신 여러 negative item을 통합하여 positive mixing과 hop mixing을 통해 hard negative를 합성한다. 그 결과 MixGCF는 GNN 기반 추천 모델의 성능 향상을 이끌어 낼 수 있었다.

대부분의 user-item 데이터의 sparsity가 높기 때문에 negative sampling이 추천 모델 성능 향상에 중요한 역할을 한다고 볼 수 있다. 해당 논문에서는 negative sampling의 품질 향상을 위한 연구를 진행하여 gnn 기반 추천 모델의 성능을 향상시킴으로서 negative sampling의 중요성을 잘 보여 주었다.

6. Reference & Additional materials

Github Implementation
- https://github.com/huangtinglin/MixGCF
Reference
- https://dl.acm.org/doi/abs/10.1145/3447548.3467408
- https://arxiv.org/abs/1806.01973
- https://arxiv.org/abs/2005.09863
- https://arxiv.org/abs/1710.09412
- https://dl.acm.org/doi/10.5555/1795114.1795167
- https://arxiv.org/abs/2002.02126
- https://arxiv.org/abs/1905.08108
- https://dl.acm.org/doi/10.1145/2484028.2484126
- https://dl.acm.org/doi/10.1145/3077136.3080786
- https://arxiv.org/abs/1811.04155