[AAAI 2019] Learning to Solve NP-Complete Problems - A Graph Neural Network for Decision TSP
Learning to Solve NP-Complete Problems: A Graph Neural Network for Decision TSP
This post is a review of “Learning to Solve NP-Complete Problems: A Graph Neural Network for Decision TSP” by Marcelo Prates, Pedro H. C. Avelar, Henrique Lemos, Luis C. Lamb, and Moshe Y. Vardi. This paper proposes a Graph Neural Network (GNN) model to solve the decision variant of the famous Travelling Salesman Problem (TSP).
1. Problem Definition
This paper investigates the decision variant of the TSP. The Traveling Salesman Problem is defined as finding the shortest possible tour visiting every node exactly once (Hamiltonian tour) on a given fully connected graph G = (V, E) composed of n vertices V and the edges E connecting them. The decision variant of the TSP is to answer whether there exists a Hamiltonian route with a cost (tour length) no larger than C on a given graph. The solution of the decision TSP is “YES” or “NO”.
2. Motivation
The aim of the paper is to bring a data-driven approach to solve the decision TSP which is an NP-Complete problem. The traditional methods require the supervision of an expert to solve the problem. The main motivation is to propose a GNN based trainable model to solve the decision TSP which removes the need for domain knowledge. In addition to that, the time required to solve the decision TSP increases substantially as the graph becomes larger. The authors claim that their model can be generalized to larger graph sizes. Lastly, the model to solve the decision TSP can be combined with traditional search methods to predict the optimal tour length of TSP.
There are existing works to solve the TSP with Deep Learning (DL) based methods. However, to the best of my knowledge, this paper is the first attempt to bring DL approach to the decision TSP. The models in the literature to solve TSP mostly focuses on the node features namely, the coordinates of the nodes. This paper sees the TSP as a graph with labeled edges where edge labels are the distance between the nodes connected. They utilize the Typed Graph Networks (TGN) based model proposed by the authors of this paper previously to assign embeddings to both vertices and edges.
3. Method
The proposed GNN-based model to solve the decision TSP inputs a TSP instance X = (G, C) composed of a graph G = (V, E) and a target cost C ∈ R and outputs the decision which is either yes or no. It assigns a multidimensional embedding to each vertex and edge in the graph representation of the problem instance through message-passing iterations. The procedure can be divided into 3 stages: generating initial edge and vertex embeddings, updating the embeddings and predicting the output. At the initialization step, vertex embeddings are chosen to be equal for all vertices and seen as the parameter of the model. This is because of the fact that vertices do not have labels associated with them. However, the edges have labels which are the weights (distances) associated with them. The target cost C is also fed to each edge embedding alongside its corresponding weight. The initial embedding for an edge is generated via the projection of 2 dimensional vector of the edge weight and target cost to d-dimensional space with Multilayer perceptron (MLP). Each vertex and edge embedding is updated based on the incoming messages from its neighbors by feeding the resulting vector into a Recurrent Neural Network (RNN). Finally, updated edge embeddings are fed into an MLP to compute a logit probability corresponding to the prediction of the answer to the decision problem.
3.1 Model Training
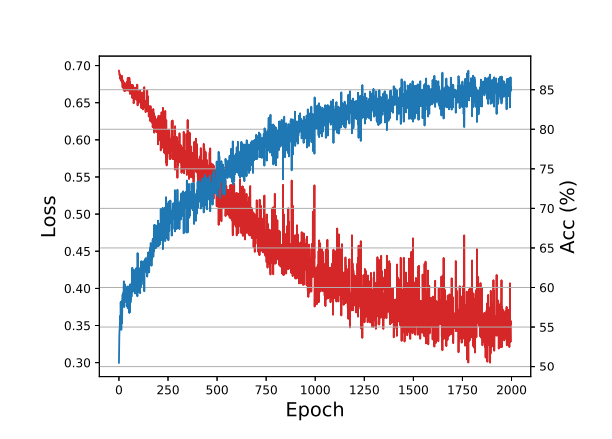
The model is trained in a supervised fashion and training instances are composed of a graph G, the target cost C and the grand truth answer which is the optimal cost of the given problem. The input grahs are generated randomly. The optimal cost is computed for each training graph using the Concorde TSP solver and then present the model with two examples containing G, one with a target cost slightly smaller than the optimal (for which the correct prediction would be NO as there is no route cheaper than the optimal) and one with a target cost slightly greater than the optimal (for which the correct prediction would be YES as there is in fact routes more expensive or equal to the optimal). Stochastic Gradient Descent (SGD) is utilized to minimize the binary cross entropy loss between the model prediction and the ground-truth. A total of $2^{20}$ instances of grah size 40 are generated for training. The evaluation of the training loss can be seen below.
4. Experimental Results and Analyses
4.1 Model Performance on Larger Instances
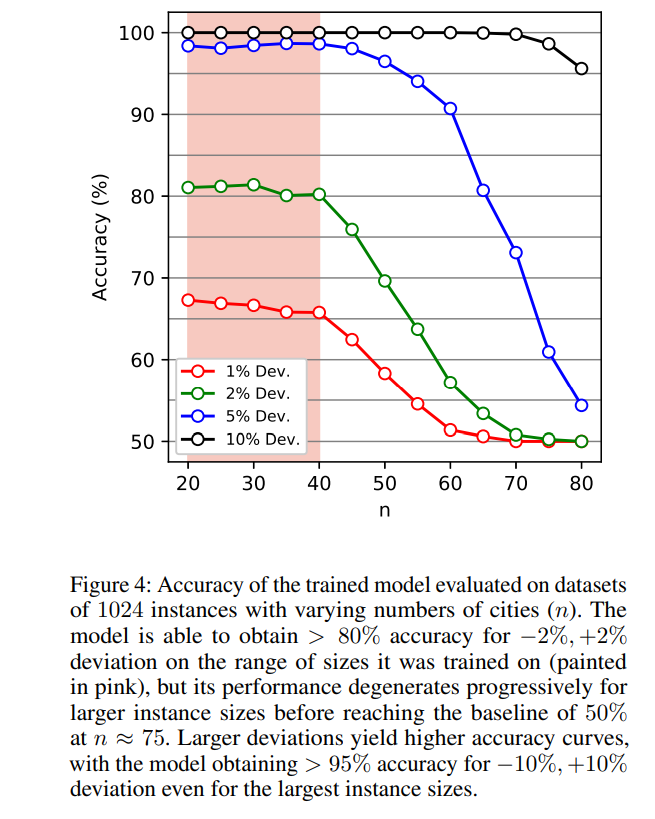
The model is originally trained on graphs of size 40 with target cost varying by 2% from the optimal. The generalization ability of the model is tested on varying graph sizes. The model sustains 80% accuracy on instances of size smaller than 40. However, its performance degrades progressively for larger problem sizes until 50% which would be the accuracy of a random prediction.
4.2 Generalizing to Larger Deviations
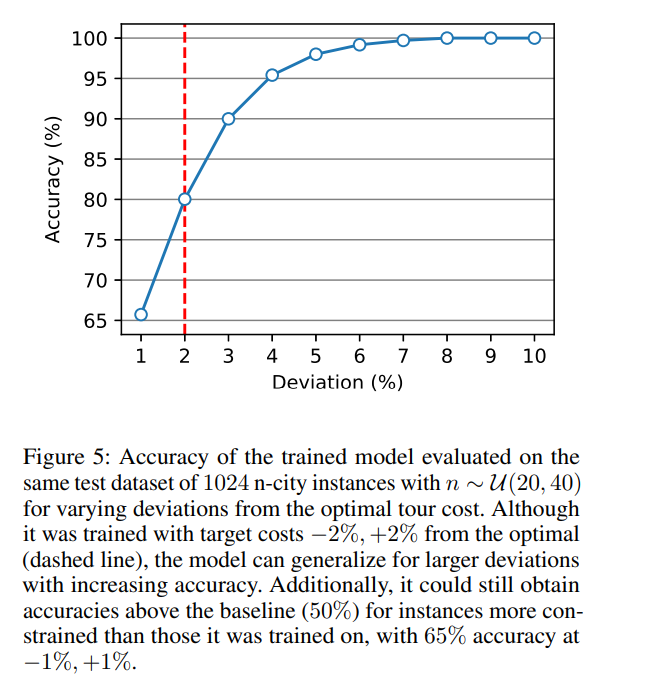
The model achieved 80.16% accuracy averaged over the training set and 80% accuracy on a testing set of 2048 instances it had never seen before. Instances from training and test datasets were produced with the same configuration (n ∼ U(20, 40) and 2% percentage deviation).
The generalization ability of the model to larger deviations is tested by observing the accuracy of the model on the same graphs in the test set but with target costs with varying deviations from the optimal cost. The model accuracy increases as the deviation from the optimal increases.
4.3 Baseline Comparison
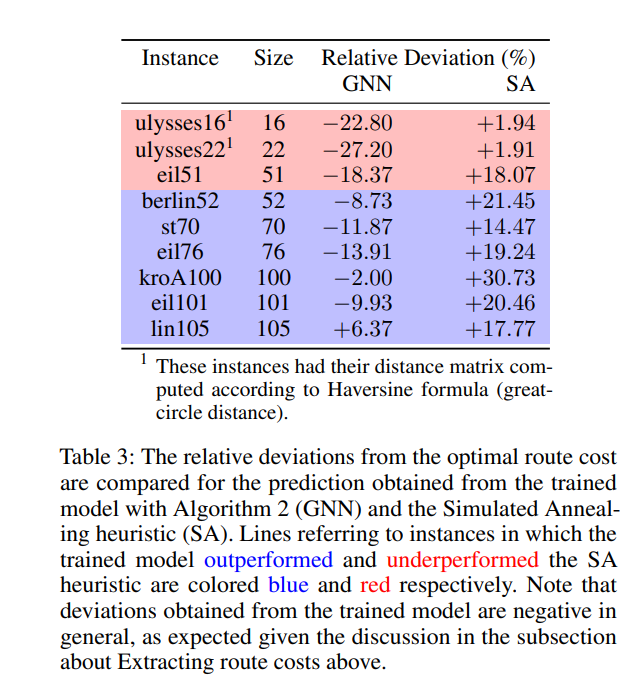
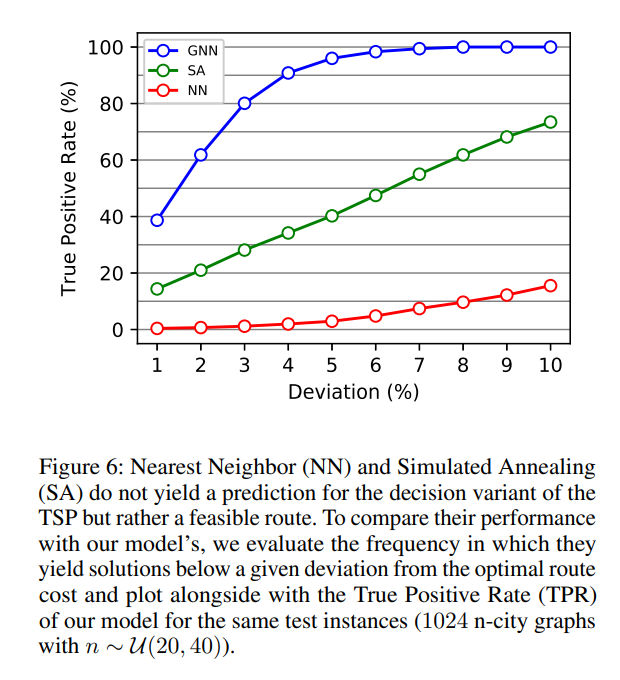
The proposed method is intended to be tested against baselines. However, this is not a straightforward task because of the lack of baseline methods for the decision TSP. Therefore, the classical baselines Nearest Neighbor (NN) and Simulated Annealing (SA) to solve TSP are adapted to create solutions for the decision TSP. This was done by measuring, for a given decision instance X = (G, C) the frequency with which either of these algorithms produced a solution with a cost no greater than C. This frequency is compared with the True Positive Rate (TPR) of the proposed model. The TPR is chosen instead of the accuracy since the classical baseline methods cannot decide that there is no shorter path since they construct a solution for the TSP. The results below show that the proposed method outperforms both methods.
5. Conclusion
A GNN based model is proposed to solve the decision TSP problem. The model generates embeddings for the vertices and edges of a given graph via message passing iterations and utilizes these embeddings to answer whether it is possible to find a Hamiltonian path on the graph with a smaller cost than target cost C. The training is performed on dual decision instances, + and - x% deviations, of a given optimal cost. The model admits 80% accuracy when it is trained on instances with 2% deviations. The experiments also showed that it generalizes to the larger deviations and varying problem sizes to some extent. The work presented in the paper is one of the first attempts to solve decision TSP with a Deep Learning method which makes it meaningful for the Combinatorial Optimization research community. The authors provided the training and model architecture details and performed several experiments to show the validity of their method. However, I think the baseline comparison part is not a fair comparison since the standard methods were not designed to solve the decision TSP. The paper also mentions shortly that the same model can be used to predict the optimal tour length of a given graph but I excluded that part in my review since the details of implementation was not satisfactory and there were no solid comparison results with the baseline methods. Lastly, one takeaway from this paper would be the graph representation of the TSP. Most of the existing works on deep learning based approaches to solve TSP use the coordinates of the nodes to represent the graph. On the other hand, this paper views the TSP graph as edge labeled graph with labels being the distance between the nodes and assuming that the initial embeddings for the vertices are equal. I personally think that this perspective better fits the nature of a TSP graph and might be providing a hint to improve the existing methods to solve TSP.
Author Information
- Marcelo Prates
- Institute of Informatics, UFRGS, Porto Alegre, Brazil
- Pedro H. C. Avelar
- Institute of Informatics, UFRGS, Porto Alegre, Brazil
- Henrique Lemos
- Institute of Informatics, UFRGS, Porto Alegre, Brazil
- Luis C. Lamb
- Institute of Informatics, UFRGS, Porto Alegre, Brazil
- Moshe Y. Vardi
- Dept. of Computer Science, Rice University, Houston, TX
6. Reference & Additional materials
- Github Implementation
- https://github.com/machine-reasoning-ufrgs/TSP-GNN.
- Reference
- https://arxiv.org/abs/1809.02721
- https://www.lume.ufrgs.br/bitstream/handle/10183/199216/001100446.pdf?sequence=1