[AAAI 2024] Learning to Optimize Permutation Flow Shop Scheduling via Graph-based Imitation Learning

1. Introduction

스케줄링은 제조 시스템에서 job의 순서와 양을 배열, 제어 및 최적화하는 방법입니다. 해당 논문에서는 자주 발생하는 최적화 문제인 Permutation Flow Shop Scheduling(PFSS)을 해결하기 위해 머신 러닝을 활용합니다. PFSS는 여러 작업을 일련의 기계에서 순서대로 생산하는 것으로 가장 포괄적으로 연구된 스케줄링 문제 중 하나입니다. 여기서 Permutation은 모든 작업물의 설비 순서가 동일한 것을 의미하고, non-permutation은 작업물이 모든 설비를 경유하지만 순서는 다를 수도 있는 것을 의미합니다.
일반적으로 PFSS의 목표는 작업의 최적 스케줄을 찾는 것으로, 총 처리 시간을 최소화하는 것을 목표로 합니다. 단일 기계의 경우, 이 PFSS 문제는 쉽게 해결할 수 있습니다. 그러나 n개의 작업과 m개의 기계(n ≥ 2)가 있는 PFSS 문제의 경우, 가능한 해는 n!개입니다. 따라서 PFSS는 NP-hard인 조합 최적화(combinational optimization, CO) 문제입니다.
해당 논문에서는 Imitation Learning(IL)을 활용하는 것을 제안하며 이 기법을 활용해 PFSS 문제를 해결하는 최초의 연구입니다. job의 수를 1000개까지 확장하고, 그래프 구조로 더 나은 표현 능력을 보여주며 빠르고 효율적인 수렴을 가능하게 합니다.

기존 접근 방식의 한계점은 다음과 같습니다.
1. 최적화 알고리즘
  - PFSS 문제는 수학적 모델링 가능하며 branch & bound, branch & cut 과 같은 정확한 방법으로 optimal solution을 구할 수 있습니다. 하지만 이러한 방법은 매우 많은 시간이 소요되기 때문에 작은 크기의 문제만 문제 해결이 가능합니다.
  - Random search, Iterated local search, NEH 등 여러 휴리스틱 알고리즘을 활용한 방법이 있지만 이러한 방법은 job의 수가 많아질수록 시간이 굉장히 많이 소요됩니다.
2. 강화학습
  - 강화 학습은 random initialization에서 시작하여 환경을 탐색하면서 최적의 의사결정을 학습합니다. 이 과정에서 많은 에피소드를 학습해야 하기 때문에 수렴 속도가 느리고, 학습 시간이 길어집니다.
  - PFSS에서 가장 좋은 성능을 보여주는 actor-critic(Pan et al. 2021) 모델은 2개의 네트워크가 필요하며 이는 학습시 많은 computational cost가 발생합니다.
  - RL 방법은 수렴해서 학습이 됐다고 하더라도 최적해를 보장하지 않으면서 정확도의 한계가 있습니다.

2. Problem descriptions

PFSS의 목표는 job의 makespan을 최소화하는 최적의 permutation을 찾는 것입니다.
Input : Processing time $X_ {m \times n}$
Output : optimal permutation $τ^{*} = [τ^{*}_ {0}, τ^{*}_ {1}, … ,τ^{*}_ {n-1}]$
Assumption 1) 시작시간은 0이라고 가정 2) 하나의 machine은 하나의 job만 처리 가능 3) 모든 작업은 각 기계에서 한 번만 처리 4) 모든 작업은 동일한 작업 순서를 공유 5) 작업이 시작되면 중단 될 수 없음
Mixed-integer Programming Model
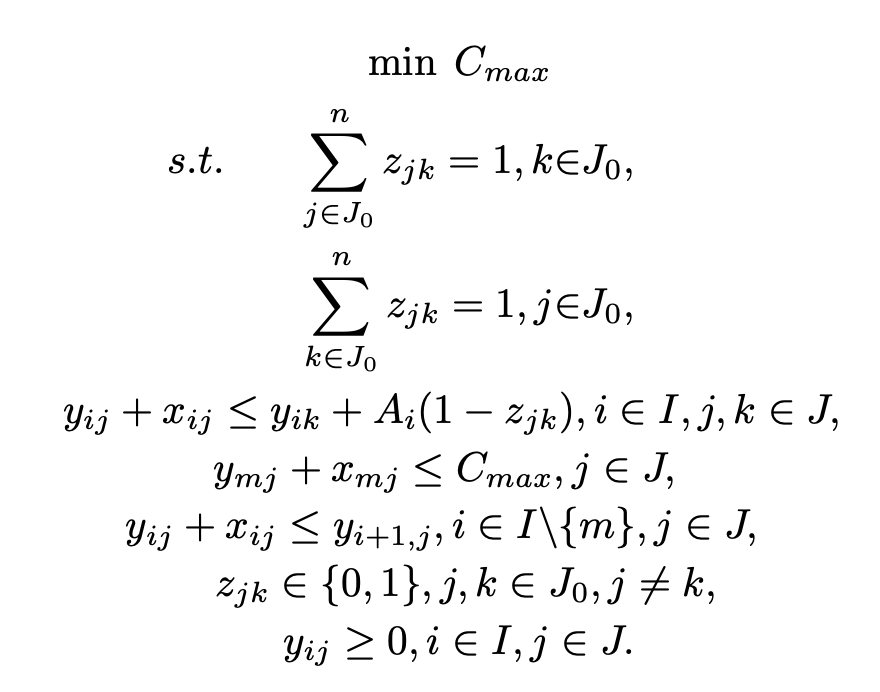
제약 조건은 각 작업이 하나의 선후행 관계를 가지고, 한 machine은 한 번에 하나의 job만 처리할 수 있습니다. job j가 job k보다 앞서면 machine i에서 job k의 시작 시간이 작업 j의 완료 시간을 넘지 않아야 함을 나타냅니다. makespan이 마지막 machine에서 모든 작업의 오나료 시간보다 크거나 같아야 합니다. 또한, job이 이전 machine에서 처리를 되지 못했으면 다음 machine에 할당이 불가능합니다.

3. Proposed method

해당 논문에서는 PFSS을 Markov Decision Process(MDP)로 정의하고, encoder-decoder policy network를 보여줍니다. policy network 학습은 Imitation Learning(IL)을 통해 진행됩니다.

3.1 Markov decision process for PFSS

PFSS 문제는 n개의 job을 스케줄링 하는 것으로 하나의 Job을 스케줄하는 것이 한 단계의 decision이라면, 하나의 n-job PFSS를 스케줄링하기 위해 만들어진 연속적인 n단계의 결정은 MDP로 볼 수 있습니다. PFSS 해결 과정을 환경으로 보고, 스케줄링 방법을 에이전드로 설정하면, state, action, policy는 다음과 같습니다.
$state$ $s_t$ : 스케줄링의 현재 상태로 이미 스케줄된 작업과 남은 스케줄링 작업을 $[V_t, U_t]$로 표현합니다. $t \in {0,1,2,…,n}$
$action$ $a_t$ : 스케줄이 아직 할당되지 않은 job set $U_t$에서 다음에 처리할 job index를 선택합니다. 이 action은 마마스킹 메커니즘을 포함한 policy network에 의해 결정됩니다. 마스킹 메커니즘은 이미 스케줄된 작업을 다시 선택하는 것을 방지하는데 도움이 됩니다. $t \in {0,1,…,n-1}$
$Policy$ $π_ {\theta}(a\vert s_ {t})$ : policy π는 action이 어떻게 진행될지 결정하며, θ는 network의 weight를 나타냅니다. a는 action 집합입니다.

3.2 Policy network

해당 논문에서는 policy network로 encoder-decoder 구조를 사용하며 encoder로 Gated Graph ConvNets(GGCN)을 decoder는 attention 메커니즘을 사용합니다.

1) 그래프 인코더 사용의 동기

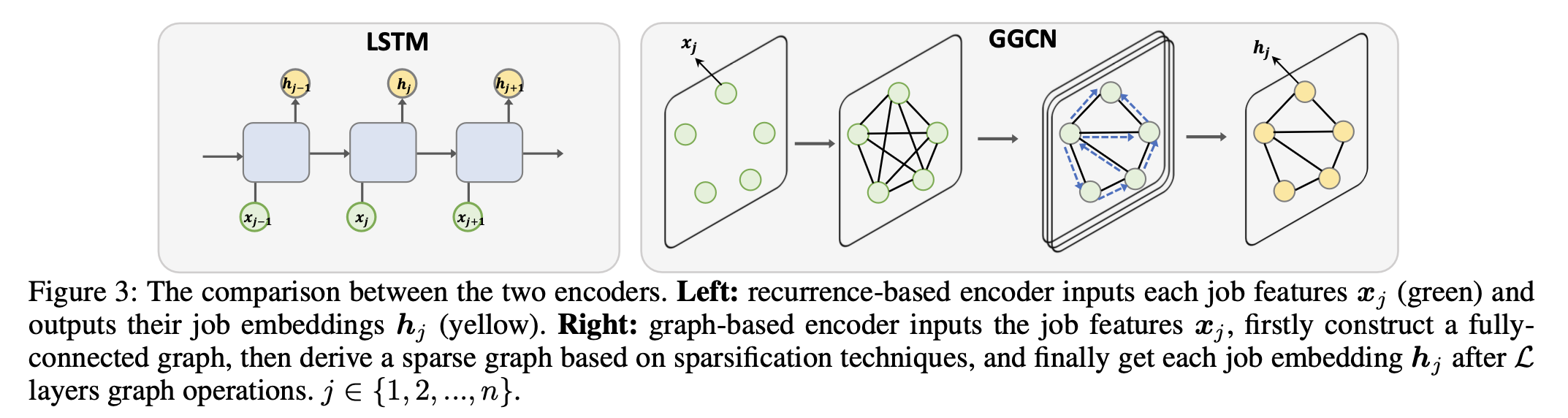
모든 작업이 동일한 특성을 가지고 있지 않으면 각 순열은 다른 makespan이 도출됩니다. 따라서 해당 논문에서는 그래프 구조를 도입하여, 한 작업의 특성을 하나의 노드로, 두 작업 간의 차이를 엣지로 사용합니다. 초기 엣지는 인접 작업 유클리드 거리의 임베딩으로 설정됩니다. 2) 그래프 인코더
n개 작업 m개 기계의 PFSS 문제에서, 입력은 모든 처리 시간을 포함하는 행렬 $X_{m×n}$입니다. 여기서 $x_{ij} ∈ X_{m×n}$은 기계 i에서 작업 j의 처리 시간을 나타냅니다. 우리는 $x_{Tj}=[x_{1j}, x_{2j}, …, x_{mj}]$를 작업 j의 입력 특성으로 사용합니다. 그림 3에서 보이듯이, 인코더는 fully connected 그래프로 시작하여 희소화 기술을 사용해 sparse 그래프를 도출합니다. 이 과정은 고정된 그래프 직경을 사용하며 각 노드를 n×20% 최근접 이웃과 기본적으로 연결합니다

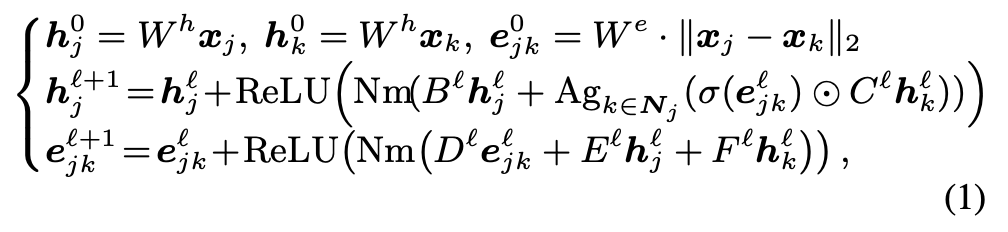
해당 논문에서는 encoder로 GGCN을 사용합니다. GGCN을 사용하는 그래프 인코더는 각 작업 j와 간선 jk에 대한 노드와 간선의 특성을 각각 $h_{ℓj}$ 및 $e_{ℓjk}$로 나타내며, 여기서 ℓ은 해당 레이어를 나타냅니다.
$h_{o,j} = W_hx_h와 h_{0,k} = W_hx_k$는 각각 작업 j와 k의 초기 노드 특성입니다. $e_{0,jk} = W_e⋅∥x_j-x_k∥_2$는 초기 edge 특성입니다. $N_m(⋅)$은 정규화 방법으로 LayerNorm 또는 BatchNorm을 의미합니다. σ는 시그모이드 함수, ⊙은 하다마르 곱(요소별 곱)입니다. $N_j$는 노드 j의 이웃 노드 집합이며, $B_ℓ, C_ℓ, D_ℓ, E_ℓ, F_ℓ$은 학습 가능한 파라미터입니다.
위 식을 통해 각 layerd에서 node와 edge의 특성을 업데이트하며, 각 노드와 이웃 간의 관계를 반영하여 특성을 추출합니다.

3) attention 디코더 사용 동기

PFSS는 feasibility 제약을 포함하고 있습니다. 디코딩 중에, 이미 스케줄된 작업은 다음 의사결정에서 제외돼야 합니다. 따라서 초기에 스케줄된 작업이 makespan에 더 큰 영향을 미칩니다. 이는 디코더에서 단순한 마스킹을 사용하는 것은 기술적으로 충분하지 않다는 것을 의미합니다. 따라서 전체적인 makespan 성능 향상을 위해 attention을 도입하고, 앞에 있는 Job에 집중합니다.

4) attention 디코더

디코더는 입력된 작업들의 집합과 이미 스케줄된 작업들의 상태를 고려하여 다음에 할당할 작업을 결정합니다. attention 메커니즘은 이미 할당된 작업에 집중하며 전체 makespan에 미치는 영향을 최적화합니다.

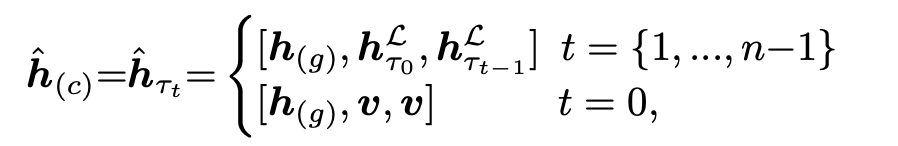
4-1) 초기 상태 및 컨텍스트 임베딩 설정 : 초기 상태 $s_0$는 모든 작업이 할당되지 않은 상태입니다. 각 시간 단계 t에서 디코더는 현재까지의 스케줄링 정보를 통합하여 컨텍스트 임베딩 $h_(c)$를 구성합니다. 이는 인코더에서 생성된 그래프 임베딩 $h_{(g)}$, 첫 작업의 $h_L^{τt-1}$을 포함하며 이 정보들은 향후 작업 선택에 필요한 컨텍스트를 제공합니다.

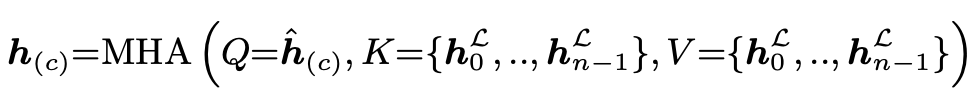
4-2) Multi-Head Attention(MHA) : MHA는 다수의 attention head를 사용하며, 다양한 정보 조각에서 중요한 정보를 추출합니다. 각 head는 다른 관점에서 정보를 처리해서 결합된 결과는 더 풍부한 정보를 반영할 수 있습니다. MHA는 쿼리(Q), 키(K), 값(V)으로 구성됩니다. MHA는 입력된 쿼리에 대해 모든 키와의 유사성을 계산하고, 이 유사성 점수를 사용하여 값들의 가중합을 계산하며 결과는 다음 작업 선택에 사용되는 컨텍스트 임베딩 $h_ {(c)}$를 생성합니다.

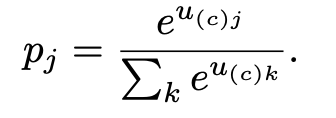
4-3) 작업 선택 및 확률 계산 : 디코더는 각 작업에 대한 logit $u_ {(c)j}$를 계산합니다. 로짓은 특정 작업이 다음 작업으로 선택될 확률에 대한 점수를 나타내며 이 점수는 attention 메커니즘을 통해 계산됩니다. 모든 로짓에 소프트맥스 함수를 적용하여 확률 분포를 얻고, 이 분포에서 가장 확률이 높은 작업이 다음 작업으로 선정됩니다.

4-4) 일반화 : 해당 논문에서는 인코딩과 디코딩 과정을 $H_ {d×n} = W^{en}_ {d×m}X_ {m×n}$ 및 $O_ {1×n} = W^{de}_ {1×d} H_ {d×n}$으로 표현합니다. 여기서 X, H, O, d는 각각 입력, 숨겨진 표현, 출력 및 숨겨진 차원을 나타냅니다. $W^{en}$과 $W^{de}$는 각각 인코더와 디코더에 대한 네트워크 가중치를 나타냅니다. $W^{en}_ {d \times m}$과 $W^{de}_ {1 \times d}$는 m과 d에만 관련이 있으며 n과는 무관합니다. 이는 모델이 n에 독립적이어서 다양한 작업 크기에 대해 일반화될 수 있습니다.

5) Imitation Learning

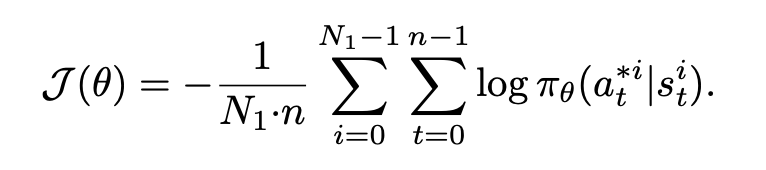
해당 논문에서는 최적화된 휴리스틱 알고리즘을 통해 얻어진 솔루션을 전문가 정책으로 설정합니다. 이 정책은 다양한 휴리스틱 방법론을 결합하여, PFSS에 대한 최적의 해결책을 제공합니다. 이후, 모방 학습은 행동 클로닝 방식을 통해 구현됩니다. 이 방법은 정책 네트워크가 주어진 전문가의 행동을 정확하게 모방하도록 학습합니다. 모방 학습에서 손실 함수는 그림과 같으며 모델이 각 시간 단계에서 전문가의 선택을 최대한 재현할 수 있도록 만드는 것입니다. 손실 함수를 최소화 함으로써, 모델은 주어진 상태에서 전문가의 행동을 선택할 확률을 극대화합니다. 결과적으로 모델은 전문가의 행동 패턴을 정확하게 학습하고, 복잡한 스케줄링 문제에 높은 성능을 발휘할 수 있도록 합니다.

4. Experiments

본 논문은 Permutation Flow Shop Scheduling(PFSS)문제를 해결하는 방법을 제안했고, 이를 평가하기 위한 다양한 실험을 설계했습니다.
1. Dataset
  
  A. randomly generated datasets : Gamma distribution과 normal distribution을 사용하여 생성된 데이터
  
  B. benchmark dataset : Taillard(Taillard, 1993)와 VRF(Vallada, Ruiz, and Framinan 2015) 벤치마크 사용
2. 비교 대상
  
  A. Heuristic Method :
  - Random search : 전역 최적화 문제 해결 기법
  - Iterated local search : 반복적으로 local search 수행하는 알고리즘
  - Iterated greedy : Initialization, Destruction, Construction, local search를 반복적으로 수행하는 알고리즘
  - NEH : Makespan을 최소화하기 위한 알고리즘으로 간단하고 효율적이어서 flow shop 에서 대표적인 비교 대상으로 선정함
  B. RL Method : Actor-Critic Method
3. 실험 결과

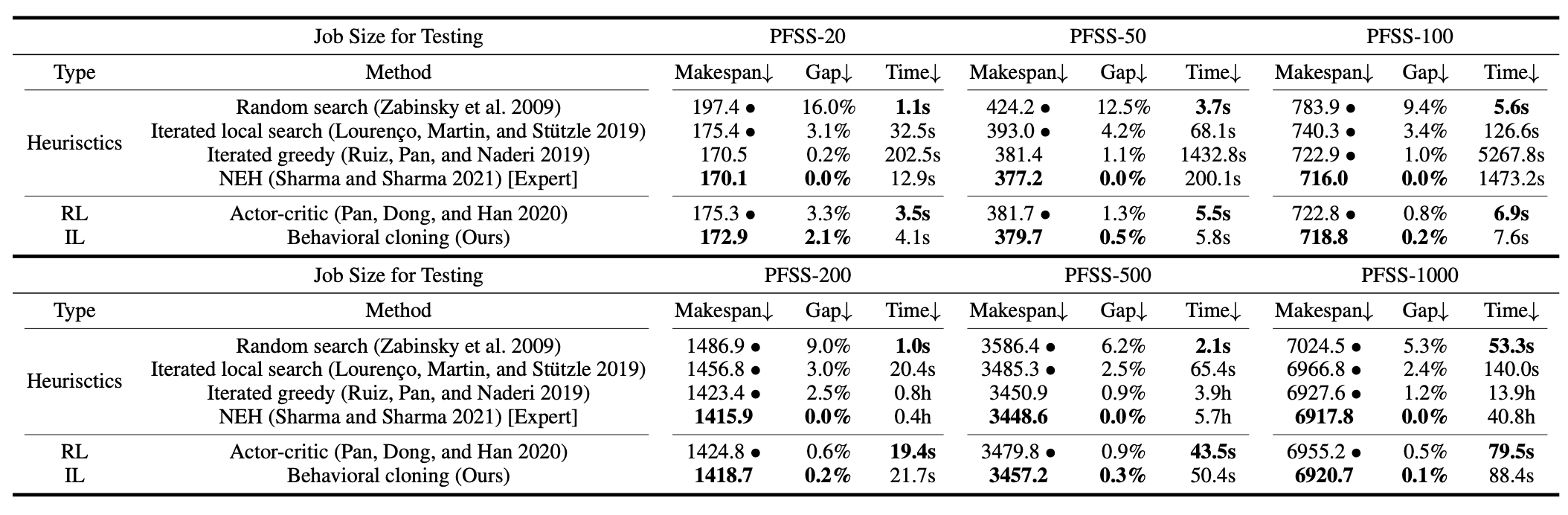
1) Table1 : Generated Datasets에 대한 실험 결과

job의 수는 20, 50, 100, 200, 500, 1000으로 설정해서 실험
job의 수가 100이하일 때는 NEH 알고리즘이 일반적으로 가장 낮은 makespan으로 가장 좋은 성능
job의 수가 늘어나도 NEH 알고리즘은 좋은 성능을 보이지만 시간이 크게 증가
강화학습 모델은 Rendom search를 제외하면 가장 우수한 속도
제안한 IL 모델은 강화학습 모델과 비슷한 속도를 가지면서 makespan은 더 우수함

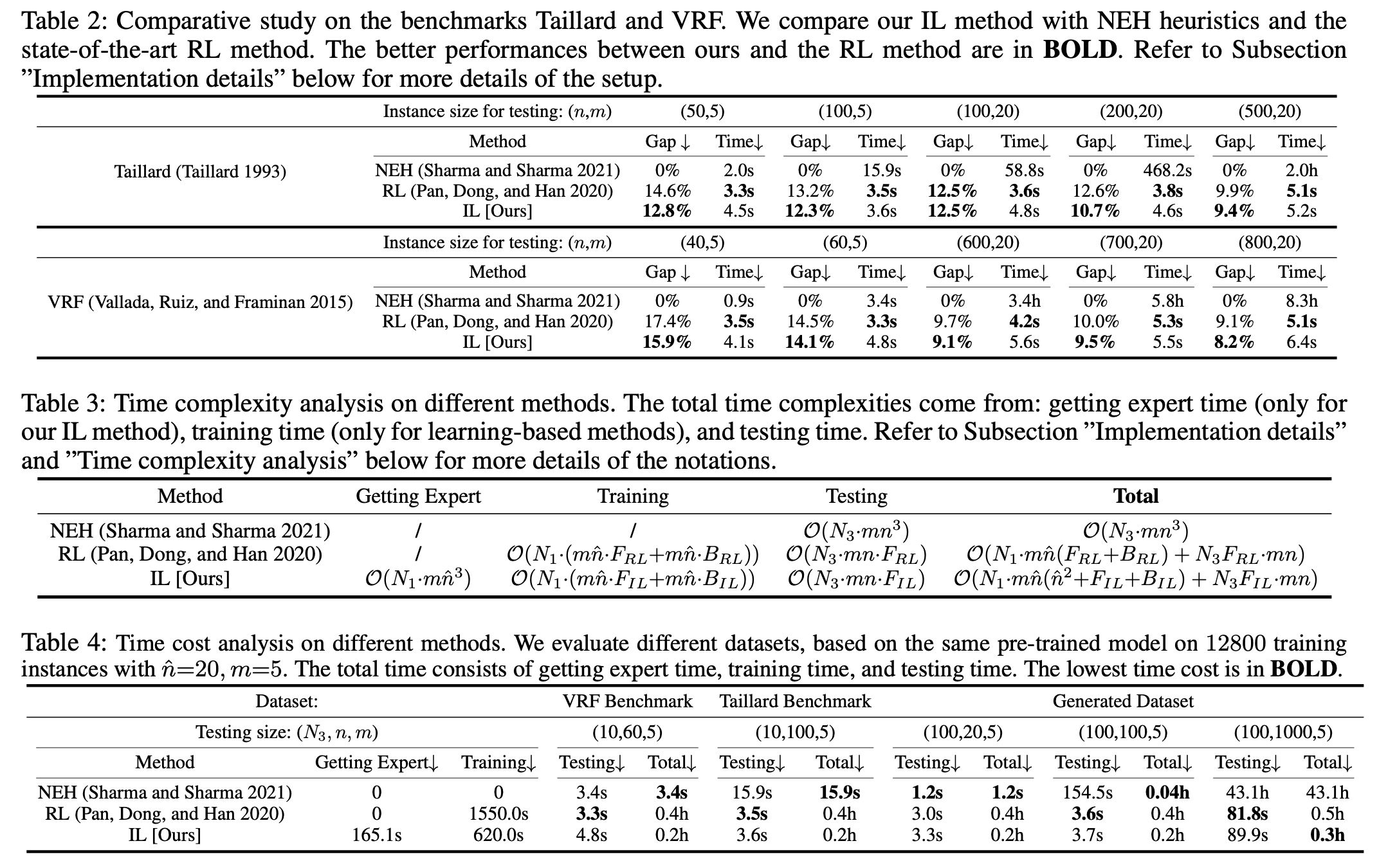
2) Table2 : Taillard와 VRF 벤치마크에 대한 실험 결과

NEH 알고리즘이 가장 낮은 makespan으로 우수함
강화 학습 모델이 처리 시간은 조금 빠르지만 정확도는 IL 모델이 우수함

3) Table3 : 각 알고리즘별 시간 복잡성 비교

NEH 알고리즘은 Test 단계에서만 복잡성이 발생
Test 단계에서 3가지 알고리즘의 시간복잡도는 유사함
Training 단계에서 RL보다 IL이 효과적임. 구조적으로 유사하지만 IL의 $F_{IL}$ $B_{IL}$은 일반적으로 $F_{RL}$ $B_{RL}$보다 작음. 왜냐하면 IL은 전문가의 행동을 모방하면서 불필요한 탐색 과정을 줄이기 때문

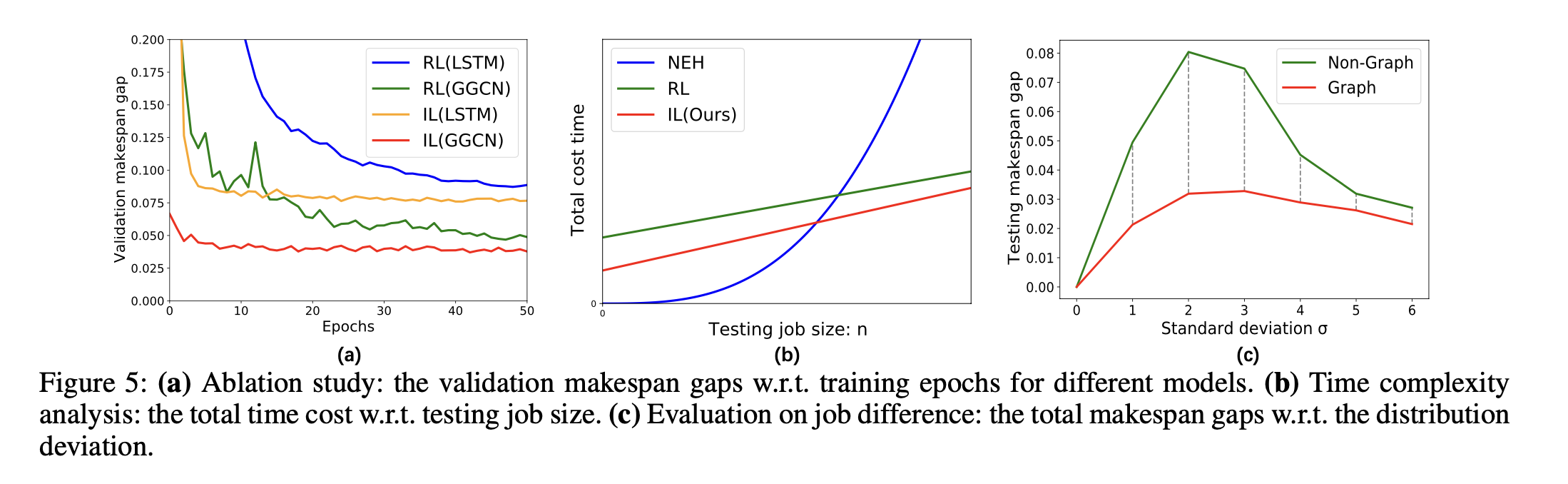
4) table4 : Total time cost 비교

job의 크기가 작을 때는 NEH 알고리즘이 가장 효율적
job의 크기가 증가할 수록 NEH의 total time cost가 크게 증가하고, RL과 IL의 time cost는 그에 비해 완만하게 증가
IL은 RL과 비교했을 때 문제의 크기가 커지더라도 RL보다 time cost가 더 작음

5. Conclusion

본 논문은 PFSS 문제를 그래프 기반 모방학습을 통해 해결하는 접근을 제시합니다. 제안된 방법의 주요 contribution은 강화 학습에 비해 더 빠르고 안정적인 수렴렴이 가능하며 기존의 RL 기반 모델에 비해 파라미터 수가 37%로 줄어들어 경량화되었습니다. 또한, 그래프 기반의 Gated Graph Convolutional Network (GGCN) 인코더를 사용하여 작업의 특성을 더 잘 표현했으며 최대 1000개의 job을 가지는 대규모 문제에서도 우수한 성능을 보여줍니다. 이는 다양한 벤치마크 데이터셋과 생성된 데이터셋에서 실험을 통해 입증되었습니다.
결과적으로 제안한 모델의 효율성, 안정성, 일반화 등 3가지 측면을 강조했고, 향후 연구에서는 더 다양하고 복잡한 스케줄링 문제에 IL 모델을 적용하는 것과 GGCN 성능 향상을 위한 다양한 그래프 구조 탐색을 할 것이라고 밝혔습니다.