[ICML 2022] How Powerful are Spectral Graph Neural Networks
How Powerful are Spectral Graph Neural Networks
이 리뷰에서 소개하는 논문 ‘How Powerful are Spectral Graph Neural Networks’는 이번 ICML 2022에서 Spotlight로 선정된 논문 중 하나입니다. 이 논문에서는 Spectral GNN의 표현력에 대한 분석 및 이를 기반으로 한 새로운 Spectral GNN 모델, ‘JacobiConv’를 소개합니다.
참고로, 이 리뷰 본문에서의 Section X.X.와 같이 어떤 section을 언급하는 부분은 리뷰 기준이고, Proposition X.X. 와 같이 어떤 Theorem 등을 언급하는 것은 논문 본문 기준임을 알드립니다.
1. Introduction
Message Passing Framework를 활용하여 이웃한 node의 정보를 aggregate 함으로써 node들의 표현(representation)을 학습하는 Graph Neural Network(GNN)는, 그동안의 Graph Representation Learning 방법론들 가운데 여러 Downstream Task에서 State-of-the-art(SOTA) 성능을 보여줬습니다.
그 한 갈래인 Spectral GNN은, Spatial한 그래프 신호(graph signal)를 Graph Laplacian을 활용해 Spectral domain으로 변환하여 필터링하고 필터링된 신호를 다시 Spatial domain으로 가져와 prediction을 수행합니다. GCN[2], GAT[3]과 같이 Popular한 모델이 등장하기 이전부터도 ChebyNet[4]과 같은 Spectral GNN이 연구되었고, 그중 GCN의 경우 ChebyNet에서의 Spectral 필터를 단순화한 모델입니다.
이외에도 이 논문에서 언급되는 여러 Spectral GNN 모델들이 등장하지만, 저자들은 이러한 Spectral GNN 모델의 표현력(expressive power)에 대해 분석하고 연구한 논문이 없었음을 지적합니다. 저자들은 이 논문을 통해 Spectral GNN 모델의 표현력에 대해 이론적인 분석을 제시하고, 이를 바탕으로 ‘JacobiConv’라는 Spectral GNN 모델을 제안합니다.
이 논문의 Contribution은 아래와 같이 정리할 수 있습니다.
- 이 논문에서는 비선형성(non-linearlity)이 없는, 간단한 형태의 Linear Spectral GNN조차도 강력한 표현력이 있음(universal함)을 이론적으로 보이며, 그런 표현력을 갖추기 위한 조건을 제시하고 이에 대해 분석합니다.
- 또한, Linear Spectral GNN의 Universality 조건과 그래프 동형 테스트(Graph Isomorphism Test; GI Test)와의 연관성에 대해서도 분석합니다. 이런 GI Test를 활용한 GNN의 표현력 분석은 Spatial한 GNN에서 다뤄진 바 있습니다[5].
- 여러 Spectral GNN의 실험적인 성능 차이를 최적화 관점에서 분석하고, 이를 통해 그래프 신호 Density에 맞는 basis function으로 그래프 신호 필터를 구성하는 것이 중요함을 보여줍니다.
- 위의 분석을 기반으로 JacobiConv라는 Spectral GNN 모델을 제시합니다. JacobiConv는 비선형성 없이도 synthetic 및 real-world dataset에서 다른 Spectral GNN baseline들을 상회하는 성능을 보여줍니다.
(주) 본문에 들어가기에 앞서, 이 리뷰는 논문의 핵심적인 개념을 위주로 서술한 것임을 밝힙니다. 이 논문은 이론적인 분석이 주가 되는 논문이기에, 이 논문에 있는 모든 Theorem, Proposition 등을 충분히 이해하기 위해서는 Specral GNN에서 포괄하고 있는 많은 배경 지식을 필요로 합니다. 다만 이 리뷰를 작성하는 저도 그러한 배경 지식이 충분하지 않기에, 이 논문에서 말하고자 하는 essential한 부분에 대해서만 다루고자 합니다. 이 점 참고하여 읽어주시면 감사드리겠습니다.
2. Preliminaries
이 Section에서는 논문 본문에서 쓰인 Notation을 그대로 서술하도록 하겠습니다. 아래는 matrix의 행, 열에 대한 Notation입니다.
$\forall M \in \mathbb{R}^{a\times b}: M_{i}=\mathrm{row_{i}}(M), M_{:i}=\mathrm{col_{i}}(M)$
그리고, 주어진 node \(i\in\mathbb{V}\)에 대해서 그 이웃을 \(N(i)\)로 표기합니다.
아래는 matrix의 condition number의 정의입니다. 이 개념은 전술했던 Contribution 3번에서의 분석과 관련이 있습니다. 여기서 \(\lambda_{max}\)는 matrix의 Maximum Eigenvalue, \(\lambda_{min}\)은 matrix의 Minimum Eigenvalue를 의미합니다.
$\kappa(M)=\frac{\vert\lambda_{max}\vert}{\vert\lambda_{min}\vert}$
이때, 주어진 matrix \(M\)이 singular(=not invertible; inverse가 존재하지 않는 경우)라면 \(\kappa(M)=+\infty\)이고, 이는 matrix의 모든 eigenvalue가 non-zero 값을 갖는 것이 matrix의 invertiblility와 동치이기 때문입니다. [6]
(주) 다만 위 정의의 경우 오류가 있는 것 같습니다. \(\vert\lambda \vert _{max}\), \(\vert\lambda \vert _{min}\) 가 맞는 표기이지 않을까 싶습니다.
아래는 Graph와 관련된 Notation입니다. Undirected graph \(\mathcal{G}=(\mathbb{V}, \mathbb{E}, X)\)가 주어졌을 때, 여기서 \(\mathbb{V}=\{1,2,\cdots,n\},\ \mathbb{E}\subset \mathbb{V}\times\mathbb{V},\ X\in\mathbb{R}^{n\times d}\)는 각각 Node set, Edge set, node feature matrix입니다.
\(A, D\)를 각각 Adjacency, Degree matrix라고 하면, normalized adjacency는 \(\hat{A}=D^{-1/2}AD^{-1/2}\)이고 symmetric normalized graph Laplacian은 \(\hat{L}=I-\hat{A}\)입니다. Graph Laplacian은 Real symmetric이기에 orthogonally diagonalizable하고, 따라서 아래와 같이 Eigen-decomposition할 수 있습니다.
$\hat{L}=U\Lambda U^{T}$
\(U\)는 \(i^{\mathrm{th}}\) column이 \(\hat{L}\)의 \(i^{\mathrm{th}}\) eigenvalue에 해당하는 eigenvector인 orthogonal matrix이고, \(\Lambda\)는 eigenvalue들을 diagonal entry들로 갖는 diagonal matrix입니다.
2.1. Graph Isomorphism
이 Section에서는 Graph Isomorphism에 대해 간략하게 다룹니다.
Graph Isomorphism은 중요한 개념이긴 하나, 이 리뷰에서는 Theorem, proposition의 증명을 상세히 다루지 않고 그 안에 담긴 의미에 대해서만 다룰 예정이기에 논문 본문에서 서술한 것 대신, 널리 알려진 정의[7]에 대해서 서술하도록 하겠습니다.
두 graph \(\mathcal{G_1}=(\mathbb{V_1}, \mathbb{E_1}, X_1),\ \mathcal{G_2}=(\mathbb{V_2}, \mathbb{E_2}, X_2)\)에 대해 bijective mapping \(f:\mathbb{V_1}\rightarrow\mathbb{V_2}\)가 존재해서, \((i,j)\in\mathbb{E_1}\)인 임의의 두 node \(i, j\in\mathbb{V_1}\)의 mapped node \(f(i),f(j)\in\mathbb{V_2}\)가 \((f(i),f(j))\in\mathbb{E_2}\)일 때 두 graph \(\mathcal{G_1},\mathcal{G_2}\)를 isomorphic하다고 하고, \(f\)를 isomorphism이라고 부릅니다.
간단하게 말하자면, 두 graph의 구조가 같은 것을 의미합니다.
2.2. Graph Signal Filter and Spectral GNNs
이 Section에서는 Graph Signal Filter와 Spectral GNN의 개념, 그리고 논문에서 주로 다루는 Linear Spectral GNN(linear GNN)에 대해 서술합니다. 그리고 Filter의 표현력에 대한 개념인 Polynomial-Filter-Most-Expressive(PFME)와 Filter-Most-Expressive(FME)에 대해서도 소개하겠습니다.
Graph Fourier Transform의 정의는 논문에서 정의된 바와 같이, (Shuman et al., 2013)[8]의 정의를 따릅니다.
Signal \(X\in\mathbb{R}^{n\times d}\)의 Graph Fourier Transform은
$\tilde{X}=U^{T}X\in\mathbb{R}^{n\times d}$
로 정의하며, inverse transform은
$X=U^{T}\tilde{X}$
와 같이 정의합니다. 여기서 \(U\)의 \(i^{\mathrm{th}}\) column은 eigenvalue \(\lambda_{i}\)에 해당하는 frequency component(eigenvector)입니다.
Eigenvalue \(\lambda\)에 해당하는 eigenvector를 \(U_{:\lambda}^{T}\)라고 하면, frequency \(\lambda\)에 해당하는 \(X\)의 frequency component를 \(\tilde{X_{\lambda}}=U_{:\lambda}^{T}X\)로 정의합니다.
이때, \(\tilde{X_{\lambda}}\neq\mathbb{0}\)라면 \(X\)가 \(\lambda\) frequency component를 갖고 있다고 정의합니다. 그렇지 않은 경우, \(\lambda\) frequency component가 \(X\)에서 missing되었다고 정의합니다.
Graph Fourier Transform과 원래 Fourier Transform의 연관성은 주어진 Signal(Graph에서는 Node feature \(X\))을 Frequency(Graph에서는 Laplacian \(\hat{L}\)의 Eigenvalue \(\lambda\)) domain으로 transform한다는 점에서 동일합니다.
또한 Fourier Transform의 경우 주어진 signal을 Function space에서의 orthonormal basis를 이용해 변환하는데, Graph Fourier Transform의 경우 주어진 signal을 vector space의 orthonormal basis인 eigenvector를 이용해 변환한다는 점에서 연관성이 있습니다.
이 이상의 Graph Fourier Transform에 대한 자세한 서술은 이 리뷰의 범위를 벗어나므로 생략하도록 하겠습니다.
(주) 이 리뷰에서 function space의 orthonormal basis에 대해서 자세히 다루는 것은 훨씬 심도깊은 논의가 필요하기 때문에 생략하도록 하겠습니다. 이와 관련하여 좀 더 알고 싶으신 분들은, Elias M. Stein and Rami Shakarchi의 Real Analysis: Measure Theory, Integration, and Hilbert Spaces (Princeton Lectures in Analysis)를 보시는 것이 좋을 것 같습니다. 또 Graph Fourier Transform에 대해서 더 자세히 알고 싶으시다면 (Shuman et al., 2013)[8]을 참고하시면 좋을 것 같습니다.
이젠 Graph Signal Filter에 대해서 서술하도록 하겠습니다. Graph Signal Filter는 signal의 frequency component를 필터링하는 역할을 수행합니다.
Filter \(g:[0,2]\rightarrow\mathbb{R}\)는 \(g(\lambda)\) 값을 각각의 frequency component에 곱해주는 방식으로 필터링을 수행합니다. Signal \(X\)에 spectral filter \(g\)를 적용하는 것은 다음과 같이 정의합니다.
$Ug(\Lambda)U^{T}X$
(주) filter의 정의역이 [0,2]인 것은 Normalized Graph Laplacian의 성질에 기인합니다.[9, Lemma 1.7.]
여기서 filter \(g\)는 \(\Lambda\)에 element-wise하게 적용됩니다. Filter를 parametrize하기 위해, \(g\)는 아래와 같이 degree \(K\)의 polynomial로 설정합니다.
$g(\lambda):=\sum_{k=0}^{K}{\alpha_{k}\lambda^{k}}$
여기서 \(g(\hat{L})\)을
$g(\hat{L})=\sum_{k=0}^{K}{\alpha_{k}\hat{L}^{k}}$
로 정의하면, 필터링 과정은 아래와 같이 표현 가능합니다.
$Ug(\Lambda)U^{T}X=\sum_{k=0}^{K}{\alpha_{k}U\Lambda^{k}U^{T}X}=\sum_{k=0}^{K}{\alpha_{k}\hat{L}^{k}X}=g(\hat{L})X$
ChebyNet 등과 같은 여러 널리 알려진 spectral GNN의 filter form은 아래 표를 통해 확인 가능합니다.

일반적으로, spectral-based GNN은 아래와 같은 form으로 정리할 수 있습니다.
$Z=\phi(g(\hat{L}))\psi(X)$
여기서 \(Z\)는 prediction, \(\phi, \psi\)는 Multi-Layer Perceptron(MLP)와 같은 함수입니다.
이때, spectral GNN의 filter가 그 어떤 polynomial filter function이라도 근사할 수 있다면, 그 GNN이 Polynomial-Filter-Most-Expressive(PFME) 하다라고 정의하고, arbitrary한 real-valued filter function을 근사할 수 있다면 Filter-Most-Expressive(FME) 라고 정의합니다.
이러한 PFME, FME property는 spectral GNN의 표현력에 있어서 중요한 성질인 것으로 보입니다. Frequency component를 scaling 함으로써 말 그대로 필터링을 해주는 Filter의 역할을 생각해봤을 때, arbitrary한 filter을 학습할 수 있느냐(=FME)는 spectral GNN의 표현력(주어진 두 node를 구별하는 능력)에 분명 큰 역할을 할 것이라고 생각할 수 있습니다.
이 논문에서는 \(\phi, \psi\)가 linear한 경우에 초점을 두고 있기 때문에, ‘Linear GNN’, linear한 spectral GNN을 아래와 같이 정의합니다.
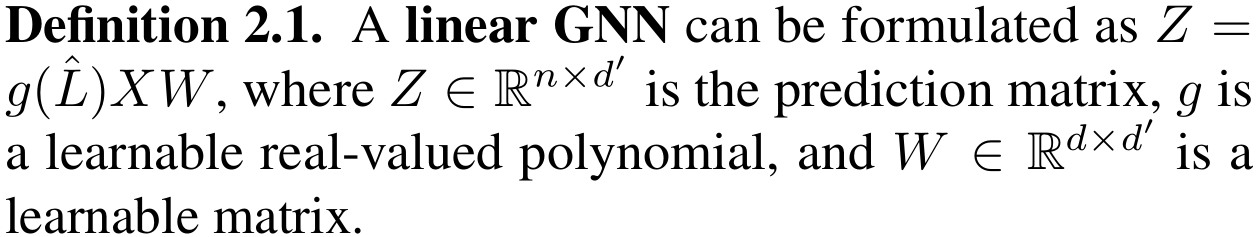
아래의 Proposition 2.2는 Linear GNN이 PFME, 즉 충분히 강한 표현력을 갖고 있고, General한 spectral GNN의 표현력의 Lower bound가 됨을 서술하고 있습니다.

비록 길었지만, 이 논문의 중요 개념을 이해하는데에 필요한 부분은 모두 짚어보았습니다. 나머지는 분석에 앞서, 이 논문에서 가정하고 있는 부분에 대한 서술입니다.
우선, 이 논문에서는 Fixed graph, fixed node features에서 오직 node property prediction task만 처리한다고 가정합니다.
위와 같은 Setting에서는 PFME=FME가 성립하게 됩니다. 왜냐하면 PFME한 GNN이 비록 polynomial filter function만 표현할 수 있지만, fixed graph setting에서는 eigenvalue \(\lambda\)가 discrete하기 때문에 arbitrary filter function을 충분히 근사할 수 있는 interpolation polynomial을 얻을 수 있고[10, Theorem 3.1., 3.3.], 이 polynomial은 PFME GNN으로 표현 가능하기 때문입니다. 이를 위해, 추가적으로 Linear GNN의 Polynomial Filter가 충분히 큰 degree \(K\)를 가지도록 설정합니다.
3. Analyses: The Expressive Power of Linear GNNs
이 Section에서는 세 가지 조건 아래에서 linear GNN이 Universal하다는 것을 증명합니다. 이어지는 3개의 sub-section에서는 세 가지 Universality 조건을 분석하여, spectral GNN이 얼마나 강력한 표현력을 가질 수 있는 지에 대해 다룹니다.
나머지 sub-section에서는 Graph Isomorphism과의 연관성(3.4.), spectral GNN에서 Non-linearlity의 역할(3.5.)에 대해 분석합니다.
본문에 들어가기에 앞서, Linear GNN \(Z=g(\hat{L})XW\)의 두 핵심 Component에 대해 다시 한 번 짚어보겠습니다.
- Linear Transformation \(W\): \(XW=U(\tilde{X}W)\)이기에, spatial domain에서의 선형 변환이 spectral domain에서의 선형 변환임을 의미합니다.
- Filter \(g(\hat{L})\): \(g(\hat{L})X=U(g(\Lambda)\tilde{X})\)이기에, filter는 frequency component를 scaling해줍니다.
이 논문의 핵심인, Linear GNN의 Universal Theorem은 아래와 같습니다.
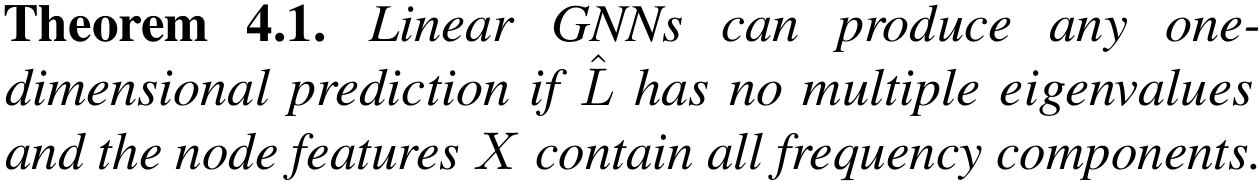
Theorem 4.1.을 통해 Universality를 얻기 위해서는 아래의 세 가지 조건이 필요하게 됩니다. 1) 1-dimensional prediction 2) Graph Laplacian has no multiple eigenvalues 3) Node feature has no missing frequency components
상기한 조건들은 linear GNN 표현력의 소위 ‘Bottleneck’이라 할 수 있습니다. 따라서 아래 sub-section들에서는 이 세 가지 Bottleneck이 되는 요소들에 대해서 자세하게 분석합니다.
3.1. About Multi-dimensional Prediction
아래 Proposition을 통해, 논문에서는 Linear GNN이 multi-dimensional prediction을 해내는 데에 있어서는 Universal하지 않다는 것을 서술하고 있습니다.

Universal Theorem을 보면 Linear GNN은 1-dimensional prediction만을 산출하는 경우에는 충분히 강력하지만, 위의 Propsition 때문에 Multiple channel을 갖는 prediction을 산출하기 위해서는 각기 다른 polynomial filter를 필요로 하게 됩니다.
이에 대해서는 Figure 1에 묘사되어 있는 Toy Example을 보도록 하겠습니다. (b), (c)를 보면, (a)에서 주어진 Node feature을 이용해 여러 dimension의 output을 만들기 위해서는 서로 다른(하나는 High-pass, 다른 하나는 Low-pass) filter가 필요하다는 것을 서술하고 있습니다.
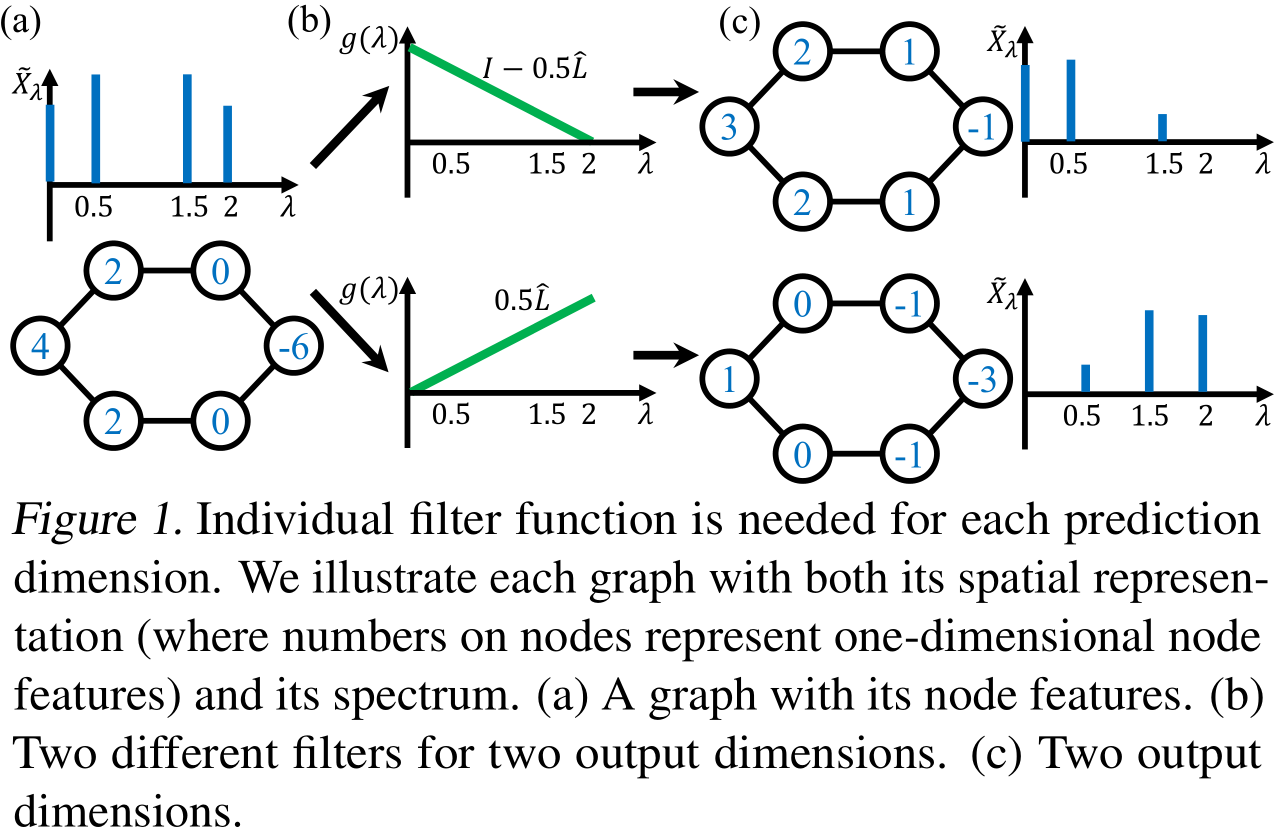
이 Toy Example을 통해서 우리는 논문에서 서술하고 있는 위의 내용 이외에도, GNN의 표현력, Universality에 있어서 arbitary filter을 근사하는 능력인 FME property가 왜 중요한 지에 대해서 생각해볼 수 있습니다. 만약 Model에서 사용하는 filter가 특정 filter를 근사할 수 없다면, 이는 특정 prediction 값을 산출할 수 없다는 것이고 다시 말해 universal하지 못하게 된다는 것을 의미합니다.
이 논문에서는 이런 Multi-dimensional prediction 문제를 각 output channel마다 다른 polynomial coefficient parameter을 사용하는 것으로 해결할 수 있다고 서술하고 있습니다.
3.2. About Multiple Eigenvalue
Graph Laplacian이 multiple eigenvalue을 갖는다는 것은 두 개의 frequency component가 같은 eigenvalue \(\lambda\)를 갖는 경우이며, 이는 다른 frequency component가 같은 scale \(g(\lambda)\)로 scaling 된다는 것을 의미합니다.
다시 말해, 서로 다른 두 frequency component를 Model이 다르게 필터링할 수 없다는 것입니다. 이런 경우 우린 Linear GNN의 표현력이 낮아진다고 생각할 수 있습니다.
이러한 Multiple eigenvalue는 주어진 graph의 topology, 즉 구조와 연관되어 있습니다.
하지만 우리는 후술된 Table 7의 데이터 통계를 통해, node feature을 갖는 real-world graph의 경우에는 이런 multiple eigenvalue가 유의미하게 적다는 것을 확인할 수 있습니다.
3.3. About Missing Frequency Components
전술했듯이, Filter는 frequency component를 scaling해주는 역할만을 수행합니다. 그렇기에 만약 node feature에서 어느 frequency component가 missing되었다면, prediction에 해당 frequency component가 반영되지 못하게 됩니다.
아래 Figure 2에는 missing frequency component가 생기는 Toy graph를 다루고 있습니다.
(주) Figure 2에 있는 1-dim node feature와 graph structure을 이용해 계산해보면, 왼쪽의 node feature로는 frequency, 즉 eigenvalue=2에 해당하는 frequency component가 0이 됩니다.
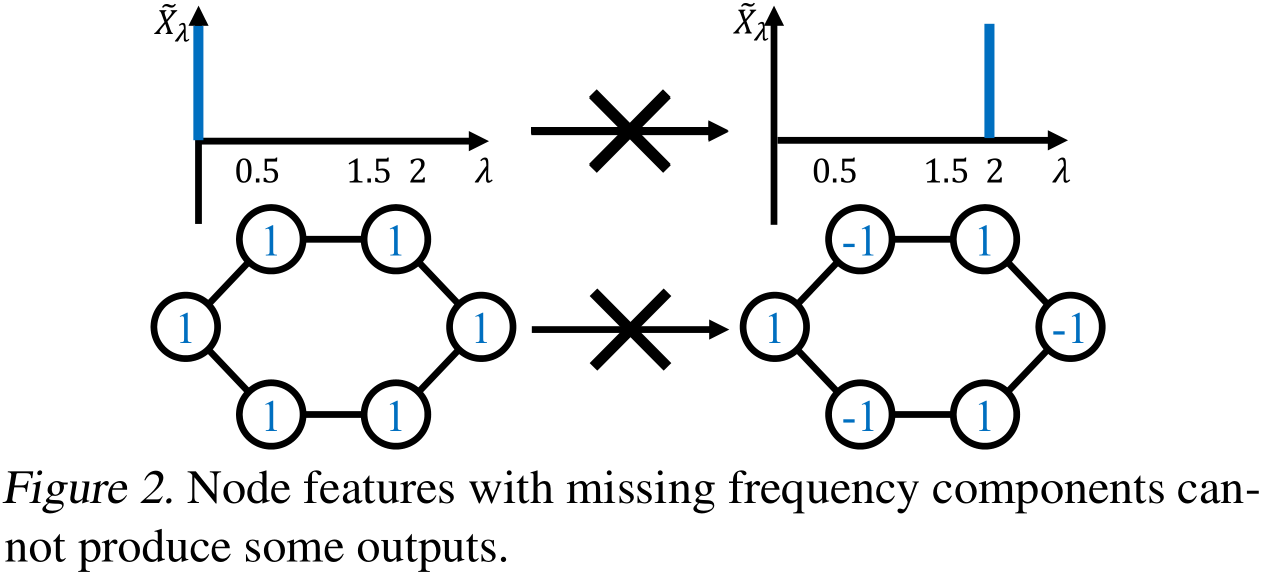
이 문제는 Graph structure(Laplacian eigenvector, 즉 frequency component에 영향)과 node feature(frequency component로 표현했을 때 없을 수 있음) 둘 다 영향을 끼치기에 다루기 어려운 문제입니다.
하지만 Multiple eigenvalue 문제처럼 이 문제 역시 real-world graph에서는 보기 어렵습니다. 아래 Table 7은 benchmark dataset에서의 multiple eigenvalue 비율과 missing frequency component의 수를 정리한 것입니다.

요약하자면, 각 output channel마다 다른 polynomial filter를 이용하는 방법과 real-world dataset의 특성을 통해 우리는 Linear GNN의 Universality를 위한 세 가지 조건이 실전에서 쉽게 만족될 수 있음을 알 수 있습니다.
3.4. About the Connection to Graph Isomorphism
Spatial GNN의 표현력에 대해 분석한 논문[5]에서는 GI test를 활용해 분석하였습니다. 이와 비슷하게 이 논문에서도 Universality 조건과 Graph Isomorphism의 연관성에 대해 분석합니다.
Graph Isomorphism Test 기법으로 언급이 되는 것이 바로 1-dimensional Weisfeiler-Lehman(1-WL) test입니다. 1-WL test는 주어진 두 graph가 isomorphic한지 판별하는 알고리즘으로, 웬만한 non-isomorphic graph들을 구별할 수 있습니다. 보다 자세한 내용은 이 링크를 참조하시면 좋을 것 같습니다.
이 논문에서는 먼저, \(K+1\) iteration 1-WL test가 구별할 수 없는 node pair는 degree $K$ polynomial filter를 갖는 Linear GNN도 구별할 수 없다는 것을 아래 Proposition을 통해 서술합니다.

Proposition 4.3.은 Linear GNN의 표현력 역시 Spatial GNN 처럼[5] 1-WL test만큼이 한계라는 것을 의미합니다.
하지만, 우리는 Universal Theorem을 통해 Linear GNN이 각기 다른 node들에 대해, 그 node들이 isomorphic한 지와 상관 없이 서로 다른 prediction을 산출할 수 있는 표현력을 갖고 있다는 것을 알고 있습니다.
또한, 1) 1-WL test는 몇몇 non-isomorphic한 node들을 구별하지 못하며, 2) 1-WL test의 경우 isomorphic한 node들에 대해 같은 label을 산출한다는 것 역시 알려져 있는 바입니다.
이렇듯 모순되어 보이는 두 사실은 Universality 조건 2와 3이 만족되면 1-WL test 역시 충분히 Powerful하다는 것(모든 non-isomorphic node를 구별할 수 있음)과 graph가 isomorphic한 node를 가질 수 없다는 것을 보여주는 결과릍 통해 해소되며, 그 결과는 아래 Corollary 4.4.와 Theorem 4.5., Theorem 4.6.에 정리되어 있습니다.

Corollary 4.4.는 Universal Theorem과 Proposition 4.3.을 통해 유도되는 결과입니다. 조건 2, 3 아래에서 1-WL test 역시 충분히 Powerful하다는 것을 보여줍니다.


Theorem 4.5., 4.6.은 조건 2, 3이 만족되면 Graph와 node feature를 제약한다는 것을 보여줍니다.
따라서 Universal Theorem의 조건을 만족한다는 것은 Graph Topology와 Node feature가 제약된다는 것을 의미하고, 1-WL test가 결국 linear GNN의 표현력의 한계라는 것을 확인할 수 있습니다. 위의 결과들을 통해서 우리는 Universality 측면에서의 spectral GNN의 표현력과 1-WL test 측면에서의 spatial GNN의 표현력 간 연결고리를 얻게 됩니다.
3.5. About the Role of Non-linearlity
우리는 앞선 결과들을 통해서 Linear GNN이 충분히 강력한 표현력을 갖고 있음을 알게 되었습니다. 그럼에도 non-linearlity는 SOTA 성능의 GNN에서 활용되고 있습니다. 이 sub-section에서는 non-linearlity가 spectral GNN에서 어떤 역할을 하는지 분석합니다.
Spectral GNN의 General form \(Z=\phi(g(\hat{L}))\psi(X)\)을 보면, Non-linearlity가 frequency component를 담고 있는 node feature를 변환하므로 node feature을 표현하는 frequency component가 바뀌게 된다는 것을 알 수 있습니다.
아래 Figure 4를 보면 더 잘 이해할 수 있습니다.
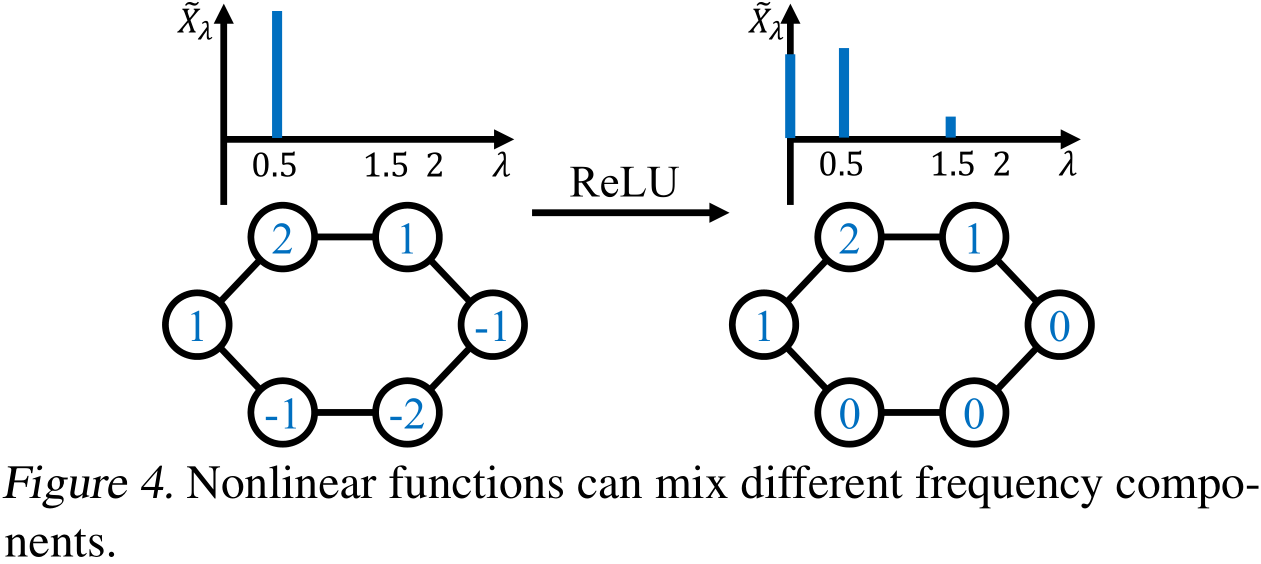
또, \(\sigma\)를 spatial signal \(X\)에 적용되는 non-linearlity라고 하면 spectral signal \(\tilde{X}\)을 transform하는 \(\sigma '\)는
$\sigma ‘(\tilde{X})=U^{T}\sigma(U\tilde{X})$
와 같습니다. 이를 자세히 보면, spectral signal \(\tilde{X}\)가 \(U\)를 통해 섞이게 된다는 것을 알 수 있습니다.
이러한 Mixing이 multiple eigenvalue, missing frequency components와 같은 문제를 어느정도 완화할 수 있을지는 몰라도, 1-WL이 spectral GNN의 표현력의 한계이기에 충분히 강한 표현력을 가질 수는 없다고 저자들은 논문에서 언급합니다. 그렇기에 이 논문에서는 Universality condition들이 real-world에서 쉽게 만족될 수 있다는 점과 이에 따른 Linear GNN의 충분히 강한 표현력을 고려하여, non-linearlity가 없는 linear GNN을 기반으로 한 모델을 제안합니다.
4. Methodology-JacobiConv
이 Section에서는 Polynomial Filter을 구성하는 Basis function 선택의 영향에 대해, Optimization 관점에서 분석합니다. 그리고 이를 바탕으로 논문에서 제안한 JacobiConv 모델에 대해 다룹니다.
\(k=0,1,2,\cdots\)에 대해 Polynomial bases를 \(g_k\)라고 정의합니다. 이 section에서는 각 output dimension에 대해 개별적인 filter parameter를 갖는 linear GNN에 대해 다룹니다. 아래는 그 formulation입니다.
$Z_{:l}=\sum_{k=0}^{K}{\alpha_{kl}g_{k}(\hat{L})XW_{:l}}$
ChebyNet에서 활용하는 것과 같은 complete한 polynomial bases들은 PFME model을 만들 수 있습니다. 하지만, 다른 bases 선택이 다른 성능을 보여준다는 것을 논문에서는 Optimization 관점에서 다룹니다.
4.1. Preliminary to JacobiConv: Hessian Matrix and Polynomial Bases choice
우선 아래와 같은 loss function으로 training한다고 가정합니다.
$R=|Z-Y|_ {F}^{2}$
추가적으로 Linear GNN이 global minimum으로 수렴할 수 있다고 가정합니다. 논문에서는 global minimum 근처에서의 수렴 속도를 분석합니다.
(주) 위와 같은 가정의 타당성은 논문의 Appendix J에 있으나, 이 리뷰에서는 다루지 않습니다.
Linear GNN의 optimization의 경우, coefficient \(\alpha\), weight \(W\) 모두 learnable한 parameter입니다. 하지만, \(W\)의 optimization의 경우, 아래의 gradient를 보면 bases와 무관함을 알 수 있습니다.
$\frac{\partial R}{\partial W_{jl}}=(g_{:l}(\hat{L})(XW)_ {:l} - Y_{:l})^{T}(g_{:l}(\hat{L})X_{:j})$
\(W\)의 gradient는 filter function 전체에 dependent합니다. 충분히 표현력 있는 bases를 활용한다면 최적점 근처에서는 filter function이 비슷하게 학습되므로 bases 선택과 weight \(W\)를 최적화하는 것은 무관합니다. 하지만, 계수 \(\alpha\)의 경우는 이와 달리 bases 선택에 크게 의존합니다. 그렇기에 bases 선택에 따른 영향을 보려면, \(\alpha\)의 optimization에 초점을 맞춰야 합니다.
Loss $R$는 convex합니다. 이때, Gradient Descent 알고리즘의 Convergence rate은 loss \(R\)의 Hessian Matrix \(H\)의 condition number \(\kappa(H)\)와 관련있다는 것[11]이 알려져 있습니다. Condition number \(\kappa(H)\)가 작을수록 수렴 속도는 빨라집니다.
Loss function이 Frobenius norm의 형태이기에, 총 loss 값은 output dimension에 걸쳐 더해지고, 각 dimension에 따라 다른 coefficient \(\alpha_{kl}\)을 사용하므로 우리는 Hessian Matrix를 dimension마다 독립적으로 분석할 수 있습니다. 그래서 output dimension \(l\)을 무시하면 Hessian matrix의 \((k_{1}, k_{2})\) entry는 아래와 같이 계산할 수 있습니다.
$\frac{\partial R}{\partial\alpha_{k_{1}}\partial\alpha_{k_{2}}}=X^{T}g_{k_{2}}(\hat{L})g_{k_{1}}(\hat{L})X=\sum_{i=1}^{n}{g_{k_{2}}(\lambda_{i})g_{k_{1}}(\lambda_{i})\tilde{X}_ {\lambda_{i}} ^{2}}$
\(\lambda\)보다 작은 frequency를 갖는 signal의 accumulated amplitude를 \(F(\lambda):=\sum_{\lambda_{i}\leq\lambda}{\tilde{X}_ {\lambda_{i}} ^{2}}\)라고 하면, 위의 Hessian entry 값은 아래와 같이 Riemann sum으로 나타낼 수 있습니다.
$\sum_{i=1}^{n}{g_{k_{2}}(\lambda_{i})g_{k_{1}}(\lambda_{i})\frac{F(\lambda_{i})-F(\lambda_{i-1})}{\lambda_{i}-\lambda_{i-1}}}(\lambda_{i}-\lambda_{i-1})$
\(n \rightarrow +\infty\) 일 때, Frequency \(\lambda\)에서의 Signal density \(f(\lambda)=\Delta F(\lambda)/\Delta \lambda\)를 이용하면 아래와 같이 Hessian entry 값을 얻을 수 있습니다.
$H_{k_{1}k_{2}}=\int_ {0} ^{2}{g_{k_{2}}(\lambda_{i})g_{k_{1}}(\lambda_{i})f(\lambda)d\lambda}$
위에서 얻어낸 결과와 \(\mathrm{argmin}_ {H}\kappa(H)=I\)라는 사실을 함께 보면, polynomial bases \(g_{k}\)가 graph signal density \(f(\lambda)\)에 대해 orthonormal할 때 condition number가 최소화되어 가장 빠르게 수렴하게 된다는 것을 알 수 있습니다.
(주) bases가 graph signal density \(f(\lambda)\) 에 대해 orthonormal하다는 것은, inner product가 \(<h,g>=\int_{0}^{2}{h(\lambda)g(\lambda)f(\lambda)d\lambda}\) 로 정의될 때 이 inner product를 갖는 함수 공간에서 orthonormal하다는 것을 말합니다.
이러한 결과는, complete한 polynomial bases들이 비록 같은 표현력을 갖고 있더라도, graph density \(f(\lambda)\)에 대해 orthonormal한 bases를 사용하는 것이 linear GNN이 가장 빠르게 수렴할 수 있게 함을 의미합니다.
4.2. Jacobi Polynomial Bases
Jacobi basis는 가장 general한 형태의 polynomial bases이며, ChebyNet에서 활용하는 Chebyshev basis의 경우 이 Jacobi basis의 특수한 형태(\(P_{k}^{-1/2,-1/2} (1-\lambda)\))라고 합니다. Jacobi basis \(P_{k}^{a,b}\)는 아래와 같이 정의됩니다.
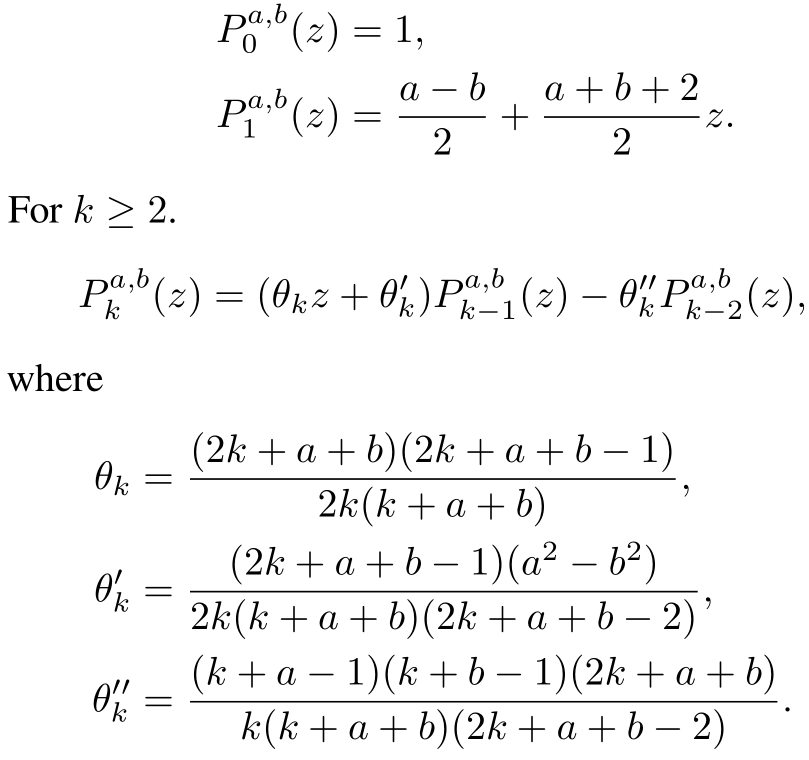
이 Jacobi basis는 weight function \((1-\lambda)^{a}(1+\lambda)^{b}\)에 대해, domain \([-1,1]\)에서 orthogonal합니다. Domain을 맞춰주기 위해, graph의 Jacobi basis는 아래와 같이 정의합니다.
$g_{k}(\hat{L})=P_{k}^{a,b}(I-\hat{L})=P_{k}^{a,b}(\hat{A})$
4.3. JacobiConv Architecture
이 sub-section에서는 논문에서 제안한 JacobiConv 모델의 Architecture에 대해 서술합니다. 먼저, node feature \(X\)의 dimension이 transformed features \(\hat{X}\)에 비해 아주 큰 경우가 많기 때문에, 먼저 \(\hat{X}=XW+b\)와 같이 Transform해주고 변환된 Signal \(\hat{X}\)를 필터링하게 됩니다.
이 논문에서는 filter에 아래의 세 가지 테크닉 1) multiple filter functions 2) Jacobi basis 3) Polynomial Coefficient Decomposition(PCD)
을 이용합니다.
먼저 첫 번째 테크닉은 Section 3.1.을 바탕으로, multi-dimensional prediction을 위해 output dimension 각각에 filter를 이용하겠다는 것입니다. 이에 따라 JacobiConv는 아래와 같이 formulate 됩니다.
$Z_{:l}=\sum_{k=0}^{K}{\alpha_{kl}P_{k}^{a,b}(\hat{A})\hat{X}_ {:l}}$
두 번째 테크닉은 Section 4.2.에서 다룬 Jacobi basis의 점화식을 이용해 필터링 연산을 수행한다는 것입니다. Formulation은 아래와 같습니다.
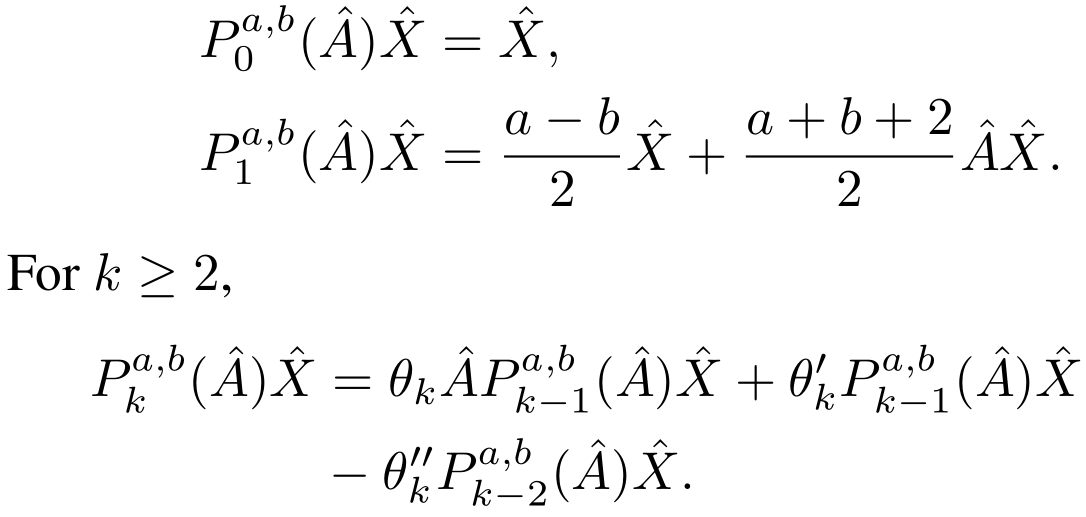
저자의 서술에 따르면, 이는 \(K\)개의 message passing 연산을 수행한다고 합니다. Form을 보면 message passing framework과 유사한 모습입니다.
세 번째 PCD 테크닉은 real-world dataset에서, \(k\)값이 커질수록 계수 \(\alpha_{kl}\)의 값이 작아진다는 observation에 기반하고 있습니다. 이렇게 계수들의 크기에 편차가 생기면 최적화가 어려워진다고 하며, 따라서 coefficient를 다음과 같이 decomposition합니다.
$\alpha_{kl}=\beta_{kl}\prod_{i=1}^{k}\gamma_{i}$
이때 \(\gamma_{i}\)는 모든 output channel $l$에서 공유되는 값입니다. \(\gamma_{i}=\gamma '\mathrm{tanh}(\eta_{i})\)로 놓으면, \(\gamma_{i}\)는 \([-\gamma ',\gamma ']\) 사이의 값을 갖게 됩니다.
이러한 parameter decomposition 테크닉을 PCD라고 부르고, 이를 기반으로 한 JacobiConv의 점화식은 아래와 같습니다.
$P_{k}^{a,b}(\hat{A})\hat{X}=\gamma_{k}\theta_{k}\hat{A}P_{k-1}^{a,b}(\hat{A})\hat{X} + \gamma_{k}\theta’_ {k}P_{k-1}^{a,b}(\hat{A})\hat{X} - \gamma_{k}\gamma_{k-1}\theta’‘_ {k}P_{k-2}^{a,b}(\hat{A})\hat{X}$
5. Experiment
이 Section에서는 논문 본문에 공유된 실험 결과에 대해 소개합니다. 논문에서는 이미지로 만든 Synthetic grid graph에서 Filter 표현력(filter를 잘 학습할 수 있는지)을 비교하는 실험과, Real-world dataset에서의 성능을 비교한 실험을 수행했습니다.
5.1. Experimental setup
-
Dataset
Filter 학습 능력을 평가하는 실험에서는 이전 연구인 BernNet[12]의 실험 세팅을 따라, 50개의 이미지를 grid graph로 변환한 Synthetic graph dataset을 사용합니다. Task는 original graph signal을 이용해 filtered signal에 fit하여, 5가지 filter function(Low, High, Band, Reject, Comb)을 잘 배울 수 있는 지를 평가하는 Regression Task입니다.
Real-world dataset의 경우, Homogeneous Graph로는 널리 쓰이는 Citation network Cora, CiteSeer, Pubmed와 2개의 Amazon co-purchase graph를 사용합니다. 추가적으로 Heterogeneous graph인 Wikipedia graph Chameleon과 Squirrel 2개, 그리고 Actor co-occurence graph, webpage graph Texas, Cornell 2개를 사용합니다. Task는 node classification이며, train/valid/test split은 60%/20%/20%입니다. -
baseline
Synthetic dataset을 활용한 실험에서는 filter 학습 능력을 평가하므로, PFME GNN들인 GPRGNN[14], ARMA[15], BernNet[12], ChebyNet[4]을 Baseline model로 사용해 JacobiConv와 비교합니다. 또한, Jacobi bases가 아닌 다른 Chebyshev, Monomial, Bernstein 등의 bases들을 이용한 linear GNN 모델과도 비교합니다. 이때, JacobiConv를 포함한 Linear GNN들은 PCD technique를 사용하지 않습니다.
Real-world dataset 실험에서는 baseline으로 다른 spectral GNN들인 GCN[2], APPNP, ChebyNet, GPRGNN, BernNet을 사용합니다. -
Evaluation Metric
Synthetic Dataset에서는 실질적으로 Regression Task이기 때문에 총 50개 graph에서의 실험 결과의 평균 MSE 값을 metric으로 활용합니다.
Real-world Dataset에서는 accuracy가 metric입니다.
5.2. Result
원래 논문에서는 아래 소개할 실험 결과 이외에도 Ablation Study, Scalability 관련 실험을 포함하고 있으나, 이 리뷰에서는 다루지 않도록 하겠습니다.
5.2.a. Synthetic Dataset Result: evaluating model on learning filters
JacobiConv가 다른 PFME GNN이나 다른 Bases를 사용한 linear GNN에 비해 Filter를 잘 학습할 수 있는지를 보여주는 실험입니다. 아래 Table 1은 다른 모델과 비교했을 때 JacobiConv의 우수성을 보여주고 있습니다. 이 실험 결과는 Section 4.1.에서의 Analysis, basis 선택이 실제 성능에 영향을 미친다는 분석을 뒷받침합니다.
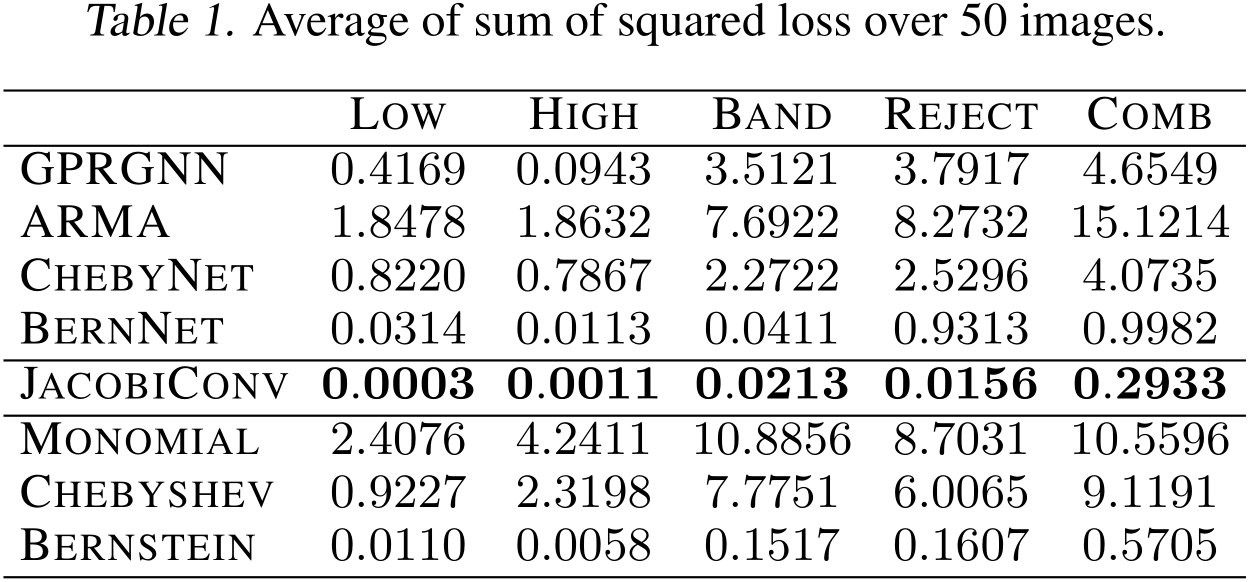
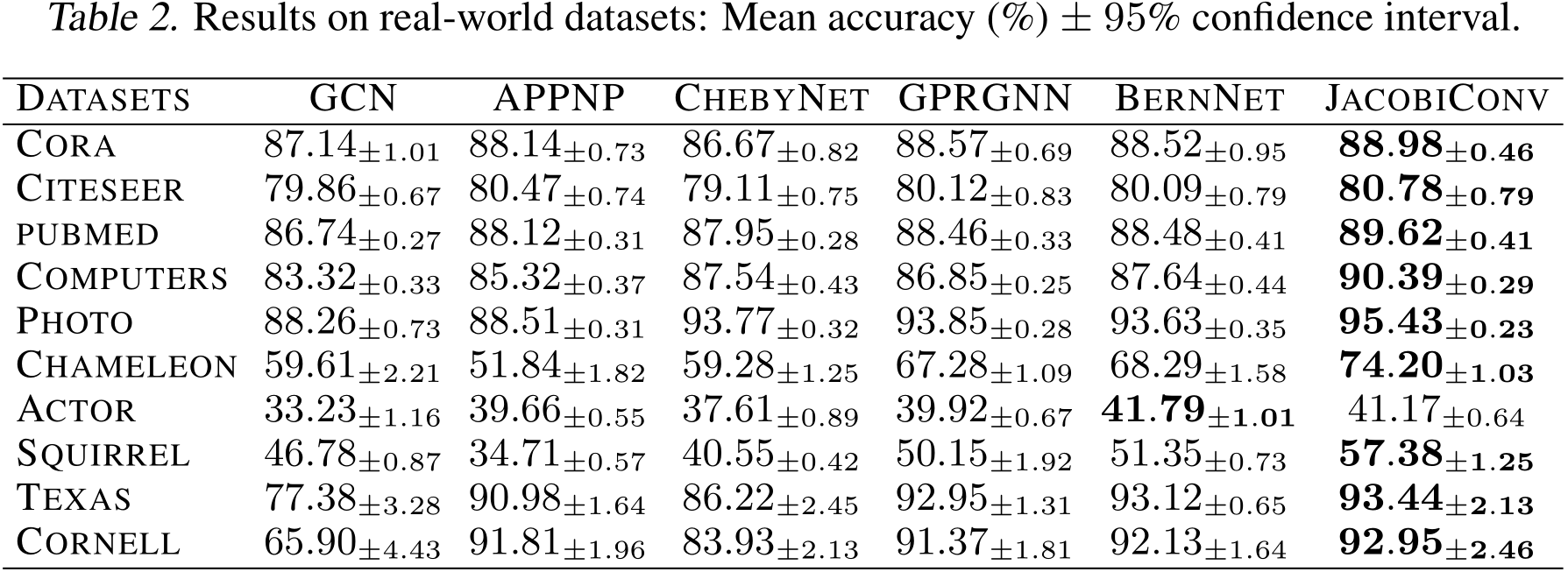
5.2.b Real-world Dataset
아래 Table 2의 결과에서 JacobiConv의 우수한 성능은 표현력이 강한 Linear Spectral GNN을 사용하는 것으로도 충분히 강력한 성능을 얻을 수 있음을 보여줍니다.
6. Conclusion
이 논문은 Spectral GNN의 Expressive Power, 표현력에 대해 이론적인 분석을 제시한 첫 연구입니다. 이미 있었던 Spatial GNN의 표현을 분석한 연구와는 다르게 주로 Universality 측면에서 표현력을 분석했지만, 이를 Spatial GNN 표현력 분석 연구에서 쓰인 Graph Isomorphism Test 측면과의 연결성 역시 제시했습니다. 또한 Spectral filter를 어떻게 구성하는 지가 실제 성능에 어떤 영향을 주는 지도 분석하였습니다.
이런 표현력에 대한 분석을 바탕으로 이 논문에서 저자들은 새로운 Spectral GNN 모델 ‘JacobiConv’를 제시하였고, 실험적으로도 우수한 성능을 보임을 광범위한 실험을 통해 입증하였습니다.
이 논문은 AI/ML 분야에서 최고 중 하나로 인정받는 학회인 ICML의 Spotlght paper로 선정된 논문입니다. 그만큼의 기대를 충족시킬만한 정말 좋은 논문이었다고 생각합니다. Problem Formulation, Theoretical Background & Analysis, Extensive Experiments 등 좋은 논문을 만드는 요소는 다 포함하고 있는 연구인 것 같습니다. 만약 Spectral GNN에 대해 관심이 있으시거나 어느정도의 배경지식을 갖고 계신 분이라면 많은 것을 얻어갈 수 있는 논문이라고 생각합니다.
가장 마음에 들었던 부분은 핵심인 Universality보다도, 최적화 측면에서 표현력이 같은 기존 spectral GNN들의 실험적 성능에 차이가 생길 수밖에 없는 이유를 분석하고 JacobiConv를 motivate한 부분이었습니다. Gradient Descent의 알려진 성질을 이용해서 왜 Filter을 구성하는 Polynomial Bases가 중요한 지에 대해 분석하고 해답을 제시한 부분에서 깊은 인상이 남았습니다.
그렇지만 이 논문에서도 아쉬웠던 부분이 없지는 않았습니다.
이 논문에서 가장 아쉬운 부분은 PFME/FME property에 대해 자세히 서술하지 않은 점입니다. 앞의 Section에서 전술했듯 Spectral GNN의 표현력은 spatial GNN에서 표현력 분석[5]에서 그랬던 것처럼 주어진 두 node를 구별할 수 있느냐 없느냐로 서술되는데(linear spectral GNN이 Universal하다는 것을 통해), 위에서 정의된 PFME, FME 성질들이 이러한 GNN의 표현력과 어떻게 연관되어 있는지에 대해서는 논문에서 직접적인 이론을 통해서 설명하지는 않았습니다.
다만, Polynomial Filter의 basis 선택이 Empirical한 성능에 중요하다는 부분을 지적하는 부분이나, 링크의 발표자료에 있는 ‘same expressive power’과 같은 맥락을 통해서 간접적으로는 PFME, FME property가 표현력과 연관이 있다고 추측해볼 수 있습니다. 그럼에도, 이 논문이 spectral GNN의 표현력을 분석하는 첫 논문이라는 점을 생각해보면 아쉬운 대목입니다. Non-PFME/non-FME spectral GNN의 표현력이 약하다와 같은 분석이 있었다면 논문의 컨텐츠가 더더욱 풍성했을 것 같아 더더욱 아쉬움이 남습니다.
이런 아쉬운 점도 있었지만, 그래도 이 논문이 갖는 가치는 엄청나다고 생각하고, Spectral GNN이라는 분야가 발전함에 있어 중요한 분기점 중 하나가 될 연구라고 생각합니다.
** Paper Author Information**
- Xiyuan Wang
- Institute for Artificial Intelligence, Peking University
- Muhan Zhang
- Institute for Artificial Intelligence, Peking University
- Beijing Institute for General Artificial Intelligence
** Review Writer Information **
- 정지형 (Jihyeong Jung)
- Master student, Department of Industrial & Systems Engineering, KAIST
7. Reference & Additional materials
The Official Implementation은 여기에서 확인 가능합니다.
- Xiyuan Wang and Muhan Zhang. How Powerful are Spectral Graph Neural Networks. ICML, 2022.
- Thomas N. Kipf and Max Welling. Semi-Supervised Classification with Graph Convolutional Networks. ICLR, 2017.
- Petar Veličković et al. Graph Attention Networks. ICLR, 2018.
- Michaël Defferrard et al. Convolutional neural networks on graphs with fast localized spectral filtering. NeurIPS, 2016.
- Keyulu Xu et al. How Powerful are Graph Neural Networks? ICLR, 2019.
- Eigenvalues and eigenvectors. Wikipedia, 2022.
- Graph Isomorphism. Wikipedia, 2022.
- David I Shuman et al. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process Magazine, 2013.
- Fan R. K. Chung. Spectral Graph Theory. Americal Mathematical Society, 1996.
- Richard Burden and J. Douglas Faires. Numerical Analysis. Cengage Learning, 2005.
- Stephen Boyd and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2009.
- Mingguo He et al. BernNet: Learning Arbitrary Graph Spectral Filters via Bernstein Approximation. NeurIPS, 2021.
- Johannes Gasteiger et al. Predict then Propagate: Graph Neural Networks meet Personalized PageRank. ICLR, 2019.
- Eli Chien et al. Adaptive Universal Generalized PageRank Graph Neural Network. ICLR, 2021.
- Filippo Maria Bianchi et al. Graph neural networks with convolutional ARMA filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.