[ICML 2020] Generalization and Representation Limits of Graph Nueral Networks
Generalization and Representational Limits of Graph Neural Networks
Introduction
Graph Neural Network (GNN) 은 graph-structured data 를 학습하기 위한 모델로 등장하여, molecular structures, knowledge graph, social networks 등 다양한 domain 에서 사용되고 있다. 본 논문에서는 GNN 의 한계와 generalization properites 에 대하여 깊게 탐구하였다. 저자는 간단한 구조의 graph 라도 GNN 이 구분하지 못할 것이라는 가정하에, 간단한 예시를 보여주며 이를 입증하였다. 또한, binary classification 에서 GNN 이 graph 의 label 을 얼마나 잘 구분할 수 있는지, 즉 graph 의 generalization bound 에 대하여 계산하고 이를 분석하였다.
Graph Neural Network (GNN) 은 graph-structured data 를 학습하기 위한 모델로 등장하여, molecular structures, knowledge graph, social networks 등 다양한 domain 에서 사용되고 있다. 본 논문에서는 GNN 의 한계와 generalization properites 에 대하여 깊게 탐구하였다. 저자는 간단한 구조의 graph 라도 GNN 이 구분하지 못할 것이라는 가정하에, 간단한 예시를 보여주며 이를 입증하였다. 또한, binary classification 에서 GNN 이 graph 의 label 을 얼마나 잘 구분할 수 있는지, 즉 graph 의 generalization bound 에 대하여 계산하고 이를 분석하였다.
저자가 GNN 을 분석한 내용은 크게 두 가지로 나눌 수 있다.
a) GNN 모델들이 특정한 graph property 에 대하여 graph 를 구분할 수 있는가?
b) GNN 모델들이 graph 의 label 을 얼마나 잘 구분해낼 수 있는가?
a) 의 경우 아주 간단한 graph 들이 주어진 상황에서 graph의 성질 (i.e., longest or shortest cycle, diameter, clique information) 을 구분하지 못하는 경우가 있음을 보여준다.
a) 의 경우 아주 간단한 graph 들이 주어진 상황에서 graph의 성질 (i.e., longest or shortest cycle, diameter, clique information) 을 구분하지 못하는 경우가 있음을 보여준다.
b) 의 경우 간단한 binary prediction 으로 graph 모델의 performance limitation 을 설명하고자 한다.
본 논문의 contribution 은 다음과 같다.
본 논문의 contribution 은 다음과 같다.
- 간단한 graph 지만, GNN 이 local information 만 사용하여 만든 embedding 으로는 구분할 수 없을 수 있음을 보인다. 또한 powerful 한 node information 을 얻어내기 위하여 “port numbering” 을 적용한 “CPNGNN” 과 “geometric information”을 사용하는 “DimeNet” 역시 해당 graph 들을 구분할 수 없음을 보인다.
- CPNGNN 을 graph theoretic 관점에서 분석하여, GNN 의 효과에 대한 insight 를 얻는다.
- GNN 의 message passing 에 관한 data dependent generalization bounds 를 제시한다. 또한, 기존 연구보다 더 tight 한 bound 임을 입증한다.
Summary
저자는 Graph 가 가지고 있는 여러 Properties 중에서, 직관적으로 이해할 수 있는 Graph Isomorphism 을 통하여, 기존 연구(LU-GNN, CPNGNN, DimeNet) 가 isomorphism 을 구분할 수 없는 Graph 가 있음을 지적한다.
즉, 간단한 예시들로 기존 연구들이 Graph Properties 를 완전히 표현할 수 없다는 한계를 보여준다.
또한, 기존 연구의 한계점을 해결하기 위한 아주 간단한 model 을 제시한다.
이 간단한 model 은 DimeNet 에 geometric information 을 추가한 것으로, Novel method 를 제안한 것이 아니라,
기존연구의 (graph isomorphism에서의) 한계를 해결하기 위한 간단한 예시를 든 것으로 이해하면 된다.
뿐만 아니라, Empirical Rademacher Complexity 로 GNN 의 bound 기존 연구보다 tight 하게 도출하는 방법을 증명하였다.
Preliminaries
- Locally Unordered GNNs (LU-GNNs): spatial information 을 사용하지 않고 각 node 의 neighbors 에서 오는 message 로 node embedding 을 updata 하는 model (e.g., GraphSAGE, GCN, GIN and GAT).
- Locally Unordered GNNs (LU-GNNs): spatial information 을 사용하지 않고 각 node 의 neighbors 에서 오는 message 로 node embedding 을 updata 하는 model (e.g., GraphSAGE, GCN, GIN and GAT).
LU-GNNs 에서 aggregation 과 conbine operation 은 다음과 같이 표기한다.
- Locally Unordered GNNs (LU-GNNs): spatial information 을 사용하지 않고 각 node 의 neighbors 에서 오는 message 로 node embedding 을 updata 하는 model (e.g., GraphSAGE, GCN, GIN and GAT).
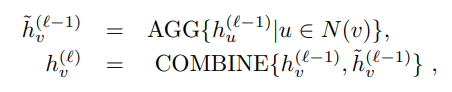
여기서, N(v) 는 node v 의 neighbor set 을 의미한다.
- Consistent port numbering GNNs (CPNGNNs): node 의 neighbors 에 port number 를 부여함으로써 local structure information 을 더 잘 뽑아내게 하는 model.
- DimeNet: molecular graphs 에서 directional message passing alogirhtm 을 사용한 model. Message passing 을 node 간의 angle 정보를 바탕으로 transform 하여 directional information 을 전달하는 model.
- Consistent port numbering GNNs (CPNGNNs): node 의 neighbors 에 port number 를 부여함으로써 local structure information 을 더 잘 뽑아내게 하는 model.
- DimeNet: molecular graphs 에서 directional message passing alogirhtm 을 사용한 model.
Message passing 을 node 간의 angle 정보를 바탕으로 transform 하여 directional information 을 전달하는 model.
- Consistent port numbering GNNs (CPNGNNs): node 의 neighbors 에 port number 를 부여함으로써 local structure information 을 더 잘 뽑아내게 하는 model.
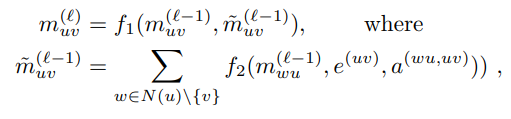
여기서 e^(uv) 는 노드 u 에서 노드 v 까지의 distance 를 의미하며, a^(wu,uv) 는 w 에서 u 까지의 거리에 wuv 의 각도를 합친 정보를 의미한다.
- Graph Property (P): Q 라는 GNN model과 서로 다른 property (P) 를 보이는 graph G_1 과 G_2 가 있을 때, 만약 f(g_Q(G_1) != f(g_Q(G_2)) 라면 model Q 는 P 를 분별할 수 있다.
또한, P 즉 graph properties 의 종류로 저자는 다음과 같은 property 를 예시로 들었다.
위의 수식은 DimeNet 의 학습 구조이며, e^(uv) 는 노드 u 에서 노드 v 까지의 distance 를 의미하며, a^(wu,uv) 는 w 에서 u 까지의 거리에 wuv 의 각도를 합친 정보를 의미한다.
- Graph Property (P): Q 라는 GNN model과 서로 다른 property (P) 를 보이는 graph G_1 과 G_2 가 있을 때, 만약 f(g_Q(G_1) != f(g_Q(G_2)) 라면 model Q 는 P 를 분별할 수 있다.
또한, P 즉 graph properties 의 종류로 저자는 다음과 같은 property 를 예시로 들었다.
1) grith (length of shortest cycle),
2) circumference (length of longest cycle),
3) diameter (maximum distance between any pair of nodes in graph),
@@ -45,94 +54,105 @@ LU-GNNs 에서 aggregation 과 conbine operation 은 다음과 같이 표기한
- Graph Property (P): Q 라는 GNN model과 서로 다른 property (P) 를 보이는 graph G_1 과 G_2 가 있을 때, 만약 f(g_Q(G_1) != f(g_Q(G_2)) 라면 model Q 는 P 를 분별할 수 있다.
Representation limits of GNNs
Limitation of LU-GNNs
저자는 LU-GNNs 을 CPNGNNs 과 비교하여, LU-GNNs 의 한계를 보여준다.
저자는 LU-GNNs 을 CPNGNNs 과 비교하여, LU-GNNs 의 한계를 보여준다.
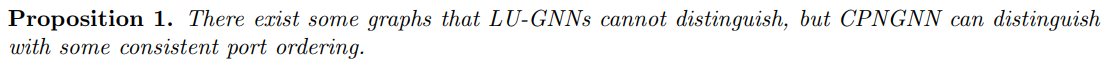
위의 Proposition 1. 을 조금 더 자세히 설명하면, LU-GNN 이 특정 property 에 대하여 구분할 수 없는 두 graph 가 존재한다고 할 때, CPNGNN 은 port numbering 덕분에 구분할 수 있다.
구분하고자하는 property 를 “Isomorphic” 으로 가정하고, 이를 그림으로 표현하면 아래의 그림처럼 표현할 수 있다.
위의 Proposition 1. 을 조금 더 자세히 설명하면, LU-GNN 이 특정 property 에 대하여 구분할 수 없는 두 graph 가 존재한다고 할 때, CPNGNN 은 port numbering 덕분에 구분할 수 있다.
구분하고자하는 property 를 “Isomorphic” 으로 가정하고, 이를 그림으로 표현하면 아래의 그림처럼 표현할 수 있다.
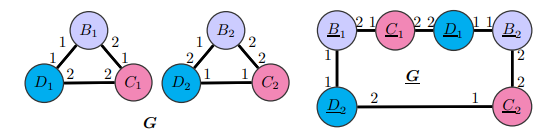
여기서 같은 색깔로 표현된 node 는 같은 feature vector 를 가지고 있다. 또한, edge 에 있는 숫자는 각 node 의 port number 를 나타낸다.
Graph G 와 G 는 isomorphic 관점에서 서로 다름을 알 수 있다. Graph G에서 structure 정보는 (B1 - C1 - D1 - B1 - C1 - D1 - B1 - …), (B2 - C2 - D2 - B2 - C2 - D2 - B2 - …) 으로 이루어져 있으며, Graph G 의 경우 (B1 - C1 - D1 - B2 - C2 - D2 - B1 - … ) 으로 이루어져있다.
하지만 LU-GNN 은 단순히 feature vector 만 사용하기 때문에, (보라색 - 빨간색 - 파란색 - 보라색 - 빨간색 - … ) 과 같은 순서로 node 가 연결되어있다는 정보만을 알 수 있다. 즉, Graph G를 (보라색 - 빨간색 - 파란색 - 보라색 - 빨간색 - …) 으로 인식하게 되며, Graph G 의 경우도 (보라색 - 빨간색 - 파란색 - 보라색 - 빨간색 - … ) 으로 인식하게 된다. 따라서, LU-GNN 의 경우 위의 그림과 같은 Graph 들의 isomorphism 을 분별하지 못한다.
CPNGNN 의 경우, port number 를 사용하기에, Graph G 에서 D2 는 port 2 를 사용하여 B2 와 연결되었다는 정보와, Graph G 에서는 D2 가 port 1 을 사용하여 B1 과 연결되었음을 알 수 있다. 따라서, CPNGNN 은 Graph G 와 G 를 isomorphism property 에서 구별할 수 있다.
여기서 같은 색깔로 표현된 node 는 같은 feature vector 를 가지고 있다.
또한, edge 에 있는 숫자는 각 node 의 port number 를 나타낸다.
Graph G 와 G 는 isomorphic 관점에서 서로 다름을 알 수 있다. Graph G에서 structure 정보는 (B1 - C1 - D1 - B1 - C1 - D1 - B1 - …), (B2 - C2 - D2 - B2 - C2 - D2 - B2 - …) 으로 이루어져 있으며, Graph G 의 경우 (B1 - C1 - D1 - B2 - C2 - D2 - B1 - … ) 으로 이루어져있다.
하지만 LU-GNN 은 단순히 feature vector 만 사용하기 때문에, (보라색 - 빨간색 - 파란색 - 보라색 - 빨간색 - … ) 과 같은 순서로 node 가 연결되어있다는 정보만을 알 수 있다. 즉, Graph G를 (보라색 - 빨간색 - 파란색 - 보라색 - 빨간색 - …) 으로 인식하게 되며, Graph G 의 경우도 (보라색 - 빨간색 - 파란색 - 보라색 - 빨간색 - … ) 으로 인식하게 된다. 따라서, LU-GNN 의 경우 위의 그림과 같은 Graph 들의 isomorphism 을 분별하지 못한다.
CPNGNN 의 경우, port number 를 사용하기에, Graph G 에서 D2 는 port 2 를 사용하여 B2 와 연결되었다는 정보와, Graph G 에서는 D2 가 port 1 을 사용하여 B1 과 연결되었음을 알 수 있다. 따라서, CPNGNN 은 Graph G 와 G 를 isomorphism property 에서 구별할 수 있다.
Limitations of CPNGNNs
CPNGNN 이 LU-GNN 이 구분하지 못하는 Graph 들을 구별할 수 있음을 보여주었다. 하지만, CPNGNN 역시 구분할 수 없는 Graph 들이 존재하며, 저자는 LU-GNN 의 limitation 을 보여주었던 것과 같은 방식으로, CPNGNN 의 limitation 을 보여준다.
CPNGNN 이 LU-GNN 이 구분하지 못하는 Graph 들을 구별할 수 있음을 보여주었다. 하지만, CPNGNN 역시 구분할 수 없는 Graph 들이 존재하며, 저자는 LU-GNN 의 limitation 을 보여주었던 것과 같은 방식으로, CPNGNN 의 limitation 을 보여준다.
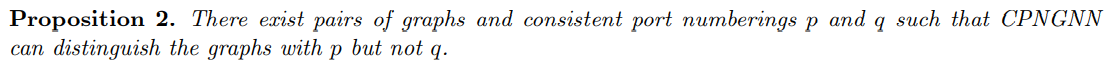
Proposition 1. 과 동일하게, 색깔은 node 의 feature vector 를 edge 의 숫자는 port number 를 나타낸다.
Proposition 1. 과 동일하게, 색깔은 node 의 feature vector 를 edge 의 숫자는 port number 를 나타낸다.
Graph 의 isomorphism property 를 구분하는 task 에서 다음 그림과 같은 Graph 들이 주어졌을 때, CPNGNN 은 isomorphism 을 구분할 수 없다.
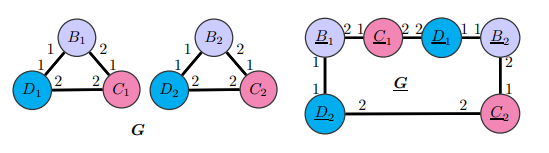
그림의 Graph 들은 Proposition 1. 에서 보인 예시에서 Port number 를 변경한 Graphs 이다.
그림의 Graph 들은 Proposition 1. 에서 보인 예시에서 Port number 를 변경한 Graphs 이다.
CPNGNN 을 사용할 때, Graph G 의 D1과 D2 와 Graph G 의 D2 가 보라색, 빨간색 feature vector 와 연결된 port number 가 같음을 알 수 있다. 따라서, CPNGNN 은 해당 그래프에서 해당 node 들을 구분할 수 없다. 따라서, 두 그래프의 isomorphism 을 구분하는데 실패하게 된다.
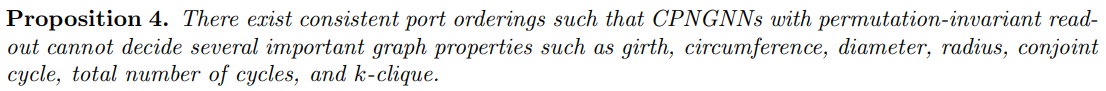
저자는 Proposition 4. 에서 isomorphism task 이외에 다른 task 에 대하여 일반화하였다.
저자는 Proposition 4. 에서 isomorphism task 이외에 다른 task 에 대하여 일반화하였다.

Graph S4 와 S8 은 girth, circumference, diameter, radius 를 가지고 있음에도 CPNGNN 이나 LU-GNN 으로 구분할 수 없다. 하지만, DimeNets 의 경우 node 간의 angle 을 사용하므로, Graph S4 의 A1-B1-C1 이 이루는 angle 과 Graph S8 의 A1-B1-C1 의 angle 이 다르기에 두 graph 를 여러 properties 에 대하여 구분 할 수 있다.
Graph S4 와 S8 은 girth, circumference, diameter, radius 를 가지고 있음에도 CPNGNN 이나 LU-GNN 으로 구분할 수 없다.
하지만, DimeNets 의 경우 node 간의 angle 을 사용하므로, Graph S4 의 A1-B1-C1 이 이루는 angle 과 Graph S8 의 A1-B1-C1 의 angle 이 다르기에 두 graph 를 여러 properties 에 대하여 구분 할 수 있다.
Graph G1, G2 의 경우 역시, CPNGNN 과 LU-GNN 으로 구분 할 수 없으나, DimeNets 의 경우 node 의 angle 정보를 사용함으로 graph 를 구분할 수 있다.
Limitations of DimeNets
DimeNets 이 CPNGNN 과 LU-GNN 이 구분할 수 없는 Graphs 들을 분별할 수 있을지라도, DimeNets 역시 구분 할 수 없는 상황이 존재한다.
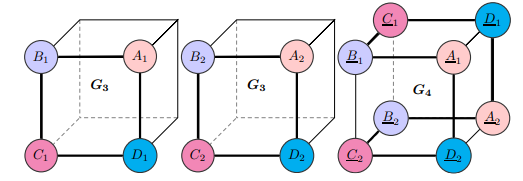
Graph G3 의 A1 과 G4 의 A1 을 비교하면 node 의 angle 정보로 G3 와 G4 를 구분할 수 없음을 알 수 있다. 따라서, DimeNets 역시 graph properties 를 구별할 수 없는 경우가 존재할 수 있다.
Graph G3 의 A1 과 G4 의 A1 을 비교하면 node 의 angle 정보로 G3 와 G4 를 구분할 수 없음을 알 수 있다. 따라서, DimeNets 역시 graph properties 를 구별할 수 없는 경우가 존재할 수 있다.
More powerful GNNs
지금까지, LU-GNN, CPNGNN 그리고 DimeNet 의 한계점에 대하여 간단한 예시를 통하여 알아보았다. 그렇다면, 이 graph models 들이 구분하지 못하는 properties 를 해결할 수 있는 model 을 구성할 필요가 있다. 저자는 이러한 model 을 아주 간단한 방식으로 구성하였다.
지금까지, LU-GNN, CPNGNN 그리고 DimeNet 의 한계점에 대하여 간단한 예시를 통하여 알아보았다.
그렇다면, 이 graph models 들이 구분하지 못하는 properties 를 해결할 수 있는 model 을 구성할 필요가 있다. 저자는 이러한 model 을 아주 간단한 방식으로 구성하였다.
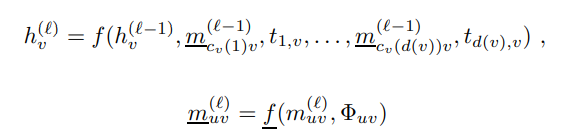
여기서 $\Phi_{uv}$ node u와 v 사이의 angle 이외의 additional geometric information 을 뜻한다. 여기서 저자는, u와 v 이외의 다른 node w, z 를 사용하여, $\Phi_{uv}$ 는 node (w,u,v) 가 이루는 plane 과 node (u,v,z) 가 이루는 plane 간의 distance 를 의미한다. 따라서 저자는 이러한 DimeNet 에서 사용하는 node angle 이외의 geometric information 사용하여 해결할 수 있다고 주장하였다.
여기서 $\Phi_{uv}$ node u와 v 사이의 angle 이외의 additional geometric information 을 뜻한다.
저자는, u와 v 이외의 다른 node w, z 를 사용하였으며, $\Phi_{uv}$ 는 node (w,u,v) 가 이루는 plane 과 node (u,v,z) 가 이루는 plane 간의 distance 를 의미한다.
따라서 저자는 이러한 DimeNet 에서 사용하는 node angle 이외의 geometric information 사용하여 해결할 수 있다고 주장하였다.
Generalization bounds for GNNs
지금까지 GNNs 의 Limitation 에 관하여 분석하였다. 본 단락부터는 저자가 GNN 의 generalization ability 에 관하여 분석한 내용을 설명하도록 하겠다.
지금까지 GNNs 의 Limitation 에 관하여 분석하였다.
본 단락부터는 저자가 GNN 의 generalization ability 에 관하여 분석한 내용을 설명하도록 하겠다.
Generalization ability 는 binary classification 에 집중하여 분석을 진행하였다.
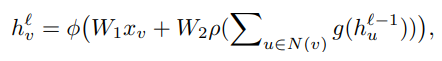
저자는 기본적인 GNN 의 embedding updata 수식 (aggretation, combine) 에서 다음과 같은 결과를 해석할 수 있다고 하였다.
- 각 node 는 각자의 embedding 을 사용하여 각자의 binary prediction 을 진행한다.
- Graph classification 에서는 node 들 각자의 binary prediction 에서로부터 majority 를 취하여 graph label 로 사용하게 된다. (average readout 때문)
- 각 node 는 각자의 embedding 을 사용하여 각자의 binary prediction 을 진행한다.
- Graph classification 에서는 node 들 각자의 binary prediction 에서로부터 majority 를 취하여 graph label 로 사용하게 된다. (average readout 때문)
Empirical Risk & Rademacher Complexity
이전의 연구에서 GNNs 의 bound 에 관하여 진행된 연구가 있다. 해당 연구는 empirical risk (\(\hat{R}\))를 사용하여, bound 를 계산하였다.
이전의 연구에서 GNNs 의 bound 에 관하여 진행된 연구가 있다. 해당 연구는 empirical risk ($\hat{R}$)를 사용하여, bound 를 계산하였다.
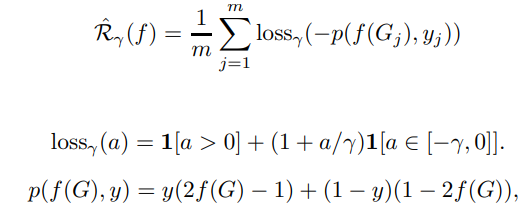
여기서 y 는 0과 1 의 binary value 를 가진다.
여기서 y 는 0과 1 의 binary value 를 가진다.
위의 식을 바탕으로, 기존 연구에 따르면 다음과 같은 GNN 의 bound 를 구할 수 있게 된다. 여기서, p 가 음수가 되는 확률이므로, population risk 의 bound (error bound) 를 의미하게 된다.
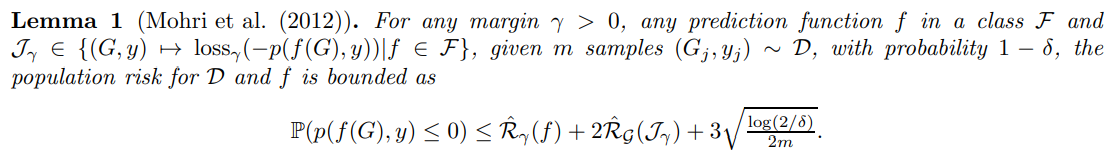
따라서, Rademacher complexity 라고 불리는 \(\hat{R}_{\mathcal{T}}(\mathcal{J}_{\gamma})\) 의 bound 를 계산하여, GNNs 의 bound 를 계산할 수 있다.
하지만, Graph 의 Rademacher complexity 를 직접 구할 수 없기에, 저자는 GNN 을 tree 형태로 표현하며 tree의 Rademacher complexity 로 Graph 의 Rademacher complexity 를 bound 할 수 있음을 보였다.
따라서, Rademacher complexity 라고 불리는 \(\hat{R}_{\mathcal{T}}(\mathcal{J}_{\gamma})\) 의 bound 를 계산하여, GNNs 의 bound 를 계산할 수 있다.
하지만, Graph 의 Rademacher complexity 를 직접 구할 수 없기에, 저자는 GNN 을 tree 형태로 표현하며 tree의 Rademacher complexity 로 Graph 의 Rademacher complexity 를 bound 할 수 있음을 보였다.
Analyzing GNN generalization via trees
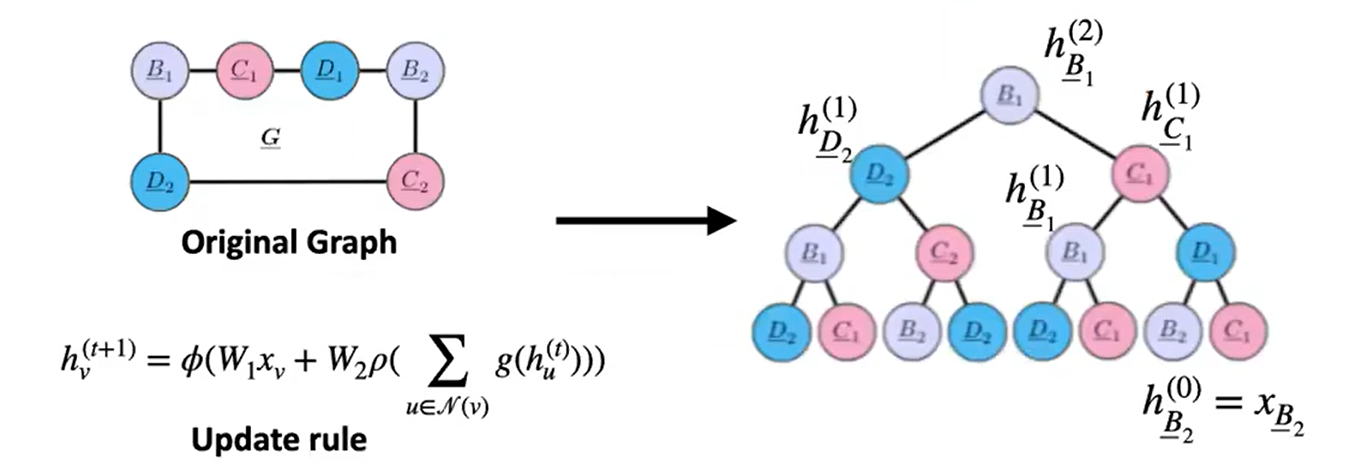
위의 그림에 따라, Graph 를 tree 로 표현할 수 있으며, 이를 통하여 몇개의 insight 를 알 수 있다.
- subtree 의 관점에서, tree node 에 대한 embedding 을 재귀적으로 표현할 수 있다.
- Shared weights 에 조그마한 변화를 주어도, tree root 의 embedding 은 거의 변하지 않는다. (individual prediction 이 거의 변하지 않는다.)
- subtree 의 관점에서, tree node 에 대한 embedding 을 재귀적으로 표현할 수 있다.
- Shared weights 에 조그마한 변화를 주어도, tree root 의 embedding 은 거의 변하지 않는다. (individual prediction 이 거의 변하지 않는다.)
GNN 을 tree 로 표현한 구조로부터 약간의 notation abuse 를 사용하여, 다음과 같이 표현할 수 있다.
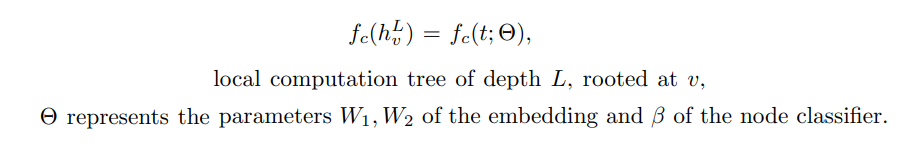
여기서 f(G;\(\theta\)) 를 tree 에 적용된 모든 function 의 expactation 으로 표기하고, T_1, T_2, … T_n 이 depth L 인 computation tree 의 모든 possible set 이라고 할때, 여기서 f(G;$\theta$) 를 tree 에 적용된 모든 function 의 expactation 으로 표기하고, T_1, T_2, … T_n 이 depth L 인 computation tree 의 모든 possible set 이라고 할때,
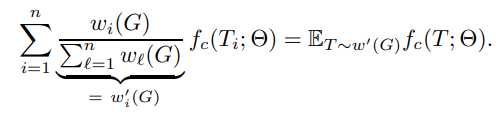
위의 식과 같이 표현할 수 있다. 즉 “GNN 의 complexity 는 computation tree 의 complexity 에 bound 될 수 있다”.
위의 식과 같이 표현할 수 있다.
즉 “GNN 의 complexity 는 computation tree 의 complexity 에 bound 될 수 있다”.
따라서, Proposition 6 을 통하여, tree 의 Rademacher complextiy 로 graph 의 Rademacher complexity 를 bound 할 수 있다.

Proposition 6 과 Lemma 1 을 사용하면 Graph 의 bound 를 알 수 있게된다. 다음 section 에서 저자는 tree 의 Rademacher complexity 를 계산하고, Graph 의 bounds 를 보여준다.
Proposition 6 과 Lemma 1 을 사용하면 Graph 의 bound 를 알 수 있게된다. 다음 section 에서 저자는 tree 의 Rademacher complexity 를 계산하고, Graph 의 bounds 를 보여준다.
Generalization Bound for GNNs
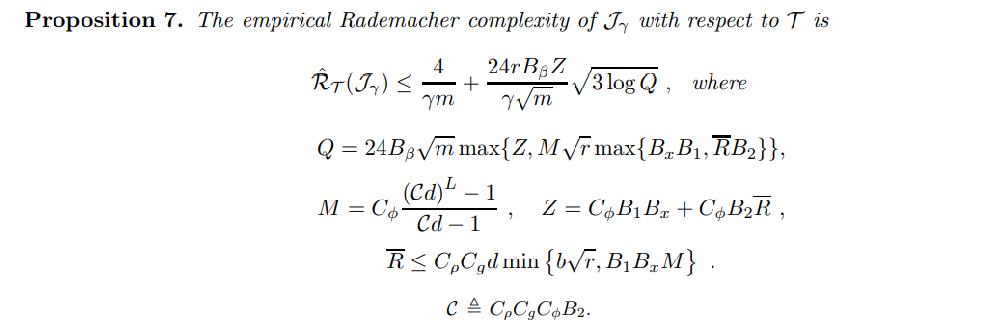
Proposition 7 을 통하여 tree 의 Rademacher Complexity 를 계산할 수 있다. 여기서 C 는 percolation complexity 를 의미하며, B_1 과 B_2 의 경우 단순하게 W1, W2 의 spectral norm 을 사용한다. Lemma 1, Proposition 6, Proposition 7 을 사용하여, 드디어 GNN 의 generalization bound 를 계산할 수 있다.
Proposition 7 을 통하여 tree 의 Rademacher Complexity 를 계산할 수 있다.
여기서 C 는 percolation complexity 를 의미하며, B_1 과 B_2 의 경우 단순하게 W1, W2 의 spectral norm 을 사용한다.
Lemma 1, Proposition 6, Proposition 7 을 사용하여, 드디어 GNN 의 generalization bound 를 계산할 수 있다.
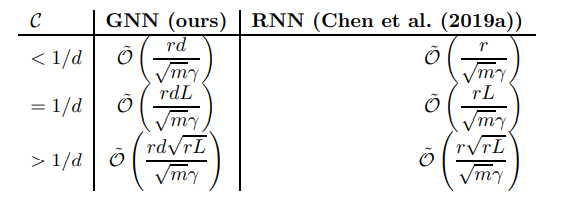
위의 표는 GNN 과 RNN 의 generalization error bound 를 C 의 값에 따라 계산한 결과이다. GNN 의 bound 를 계산할 때, tree 구조를 사용하여 계산하였기에, branching factor d 가 GNN에 추가된 모습을 확인할 수 있다. 또한, r: dependence on dimension, L: depth (in RNN length), m: sample size 를 나타낸다.
위의 표는 GNN 과 RNN 의 generalization error bound 를 C 의 값에 따라 계산한 결과이다.
GNN 의 bound 를 계산할 때, tree 구조를 사용하여 계산하였기에, branching factor d 가 GNN에 추가된 모습을 확인할 수 있다.
또한, r: dependence on dimension, L: depth (in RNN length), m: sample size 를 나타낸다.
Additional Analysis
이 외에 저자는 VC-bounds 와 저자가 계산한 GNN 을 비교하여, VC-bounds (O(r^6 N^2) , 저자 (O(r^3 N / (m^(1/2))) 로 저자의 bound 가 더 tight 함을 보였다.
Additional Analysis
이 외에 저자는 VC-bounds 와 저자가 계산한 GNN 을 비교하여, VC-bounds (O(r^6 N^2) , 저자 (O(r^3 N / (m^(1/2))) 로 저자의 bound 가 더 tight 함을 보였다.
또한, shared weight parameter 와 classifier parameter 가 변경될 때의 영향에 대한 분석을 기술하였다.

$\nabla_{L}$ 는 Weight (W1, W2) 에서 도출된 embedding 과 (W’1, W’2) 에서 도출된 embedding 의 l2-norm difference 를 보여준다.
또한, shared weight parameter (W1,W2) 와 classifier parameter (\(\beta\)) 가 변경될 때의 probability 변화를 계산하면 다음과 같다.
또한, shared weight parameter (W1,W2) 와 classifier parameter ($\beta$) 가 변경될 때의 probability 변화를 계산하면 다음과 같다.

Lemma 4 를 통하여 충분히 수렴이 되는 조건 하에서, “change in probability” 는 매우 작은 값을 가질 수 있음을 알 수 있다.
즉, Shared weights 에 조그마한 변화를 주어도, tree root 의 embedding 은 거의 변하지 않는다. (individual prediction 이 거의 변하지 않는다.)
Conclusion
본 논문은 단순 GNN 모델 (LU-GNN), CPNGNN, DimeNet 의 한계에서 대하여 직관적인 예시를 보여주며 설명하였다.
또한, GNN 의 generalization bound 를 이전의 연구 (VC-bounds) 보다 더 tight 한 결과를 얻어, GNN 의 효용을 보여주었다.
마지막으로, Shared weight parameter 의 변화가 충분히 수렴되는 상황 속에서는 model performance 에 영향을 거의 주지 않음을 증명하였다.
또한, Graph Isomorphism 에 대하여, 기존 연구가 가지고 있는 한계점을 해결하기 위한 간단한 model 예시를 보여주었다.
Graph Generalization 측면에서는, GNN 의 generalization bound 를 이전의 연구 (VC-bounds) 보다 더 tight 한 결과를 얻어, GNN 의 효용을 보여주었다.
마지막으로, Shared weight parameter 의 변화가 충분히 수렴되는 상황 속에서는 model performance 에 영향을 거의 주지 않음을 증명하였다.