1. Motivation

Graph neural network (GNN)은 Input Graph 를 적절히 표현 (represent) 하는 데 있어서 최적의 도구로 여겨졌다. Graph Convolutional Networt (GCN), Graph SAGE, Graph Isomorphism Network (GIN) 등의 대표적인 GNN 모델은 독자적으로 발전되어 왔다.

이와 별개로 Transformer 는 딥러닝 모델로써 매우 큰 성공을 거두었는데, BERT와 GPT-3 를 위시한 language model 뿐만 아니라, Vision Transformer (ViT) 까지 개발되면서, Computer Vision 에서도 Convolutional Neural Network (CNN)의 성능을 압도하였다. Transformer는 (1) Attention 구조를 통해 node 간의 relation 을 global sense에서 잘 모사할 수 있으며, (2) positional encoding 등의 구조를 통해 효과적인 inductive bias를 부여할 수 있다.

Transformer 의 압도적인 성능은 당연히 Graph Representation 영역에서도 연구적 관심을 끌기에 충분했다. 사실 이는 매우 합리적인 접근인 것이, Transformer는 사실 Graph Neural Network 구조와 매우 크게 닮아있다. Node의 관계성을 attention 으로 매핑하는 것은 fully connected graph 의 massage passing 과 굉장히 유사한 부분이 있다.

이 논문은 Transformer를 적절히 변형하여 graph representation 을 위한 transformer인 Graphormer를 개발하였다. 또한 이전의 여러 popular한 GNN 모델이 Graphormer의 특수 케이스라는 것을 증명하였다.

2. Method

1

사실 해당 논문은 매우 복잡한 테크닉과 증명이 들어있다. 이를 일일히 리뷰 하는 것은 오히려 큰 그림을 보는 시야를 해칠 수 있으므로, 이 리뷰에서는 Method의 의도와 Sketch 정도를 다루도록 하겠다. 구체적인 Technique과 증명은 논문과 코드를 참고하는 것이 좋겠다.

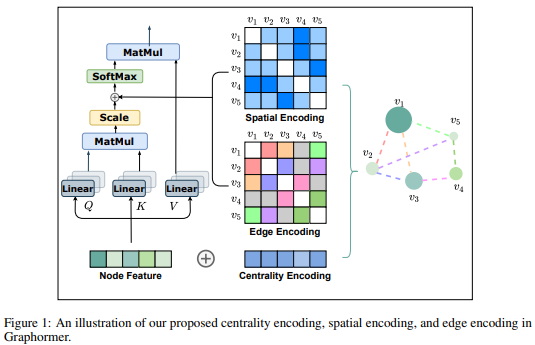
해당 방법의 핵심은 Graph 의 특징을 Transformer 구조에 얼마나 잘 녹여내느냐 이다. 크게 두가지 Novel 한 방법이 제시된다: (1) Centrality Encoding, (2) Spatial Encoding. Summary 하자면, 얼마나 Graph의 Inductive Bias를 영리하게 부여하는 지에 대한 여부이다.

2.1 Centrality Encoding

Transformer의 Attention 구조는 각 노드의 correlation 을 mapping 한다. Graph 에서는 좀 더 inductive bias를 부여해 줄 수 있는데, 그것은 node가 얼마나 많이 연결되어 있는지 (연결성)의 정도를 그 노드의 중요도로 평가할 수 있는 지점을 이용하는 방법이다. 즉 node 가 in-degree 와 out-degree가 얼마나 되는지를 compute 하여 이를 bias로 이용해 줄 수 있다. 식으로 나타내면 다음과 같다.

$ h_i^{(0)}=x_i+z_{\operatorname{deg}^{-}\left(v_i\right)}^{-}+z_{\operatorname{deg}^{+}\left(v_i\right)}^{+} $

2.2 Spatial Encoding

Image의 Spatial information 은 Euclidean space에서 쉽게 정의된다 (픽셀들간의 기하학적 거리). Language 에서도 문장의 순서가 굉장히 중요한 information 이다. Transformer에서는 이를 위해 positional encoding 을 통해 spatial encoding 을 처리한다.

Graph 에서는 당연히 edge (즉, node의 pairwise 정보)를 주목할 필요가 있다. 가장 general 한 edge bias는 node간의 shortest path 라고 볼 수 있다. 따라서 해당 논문에서는 spatial encoding

$ \phi\left(v_i, v_j\right): V \times V \rightarrow \mathbb{R} $

을 shortest path 로 사용하여 attention 구조에 bias

$ b_{\phi\left(v_i, v_j\right)} $

를 부여한다:

$ A_{i j}=\frac{\left(h_i W_Q\right)\left(h_j W_K\right)^T}{\sqrt{d}}+b_{\phi\left(v_i, v_j\right)} $

이 구조는 edge attribute 에 따라서 확장 될 수 있다. 예를들어 molecular graph 에서는 chemical bonding 도 edge로 표현 될 수 있다. 이에 대한 자세한 확장은 논문을 참조하는 것이 좋겠다.

결국 이러한 bias 부여를 통해 기존 transformer를 사실상 그대로 이용하면서 popular GNN 구조의 performance를 넘으며, 이론적인 보장까지 얻어 낼 수 있다.

3. How Powerful is Graphormer?

이 논문의 주요 contribution 중 하나는 Graphormer 가 기존 GCN, GIN, GraphSAGE의 general case라는 점을 증명한 것이다. 증명의 결과는 다음과 같다.

Fact 1. Graphormer layer는 GIN, GCN, GraphSAGE의 Aggregate, Combine step을 표현 가능하다.

Fact 2. Graphormer layer는 Mean Readout 함수를 표현 가능하다.

결국 Graphormer는 GNN의 general case다.

4. Experimental Results

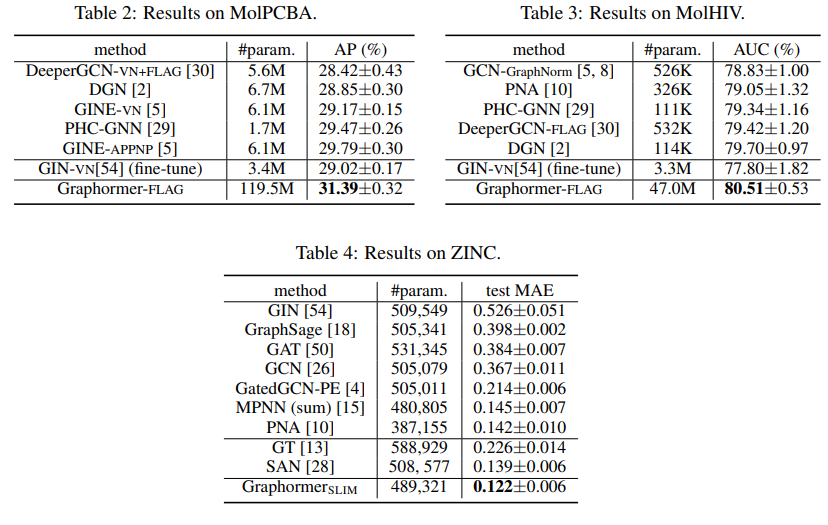
해당 방법의 performance는 매우 강력하다. 대부분의 실험은 chemical graph 의 regression task로 진행되었다.

모든 task에서 기존 GNN 구조들 (특히 SOTA method 인 GIN)을 압도하였다.

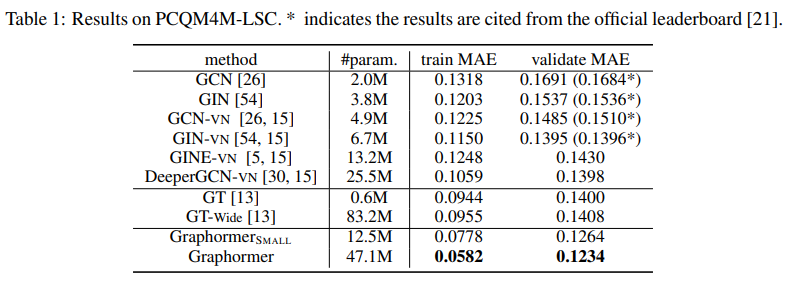
Task dataset은 PCQM4M-LSC, ogbgmolhiv, ogbg-molpcba and ZINC 에서 진행되었고, 이는 OGB chemistry regression task 의 일환이다. 놀랍게도 Graphormer는 모든 benchmark에서 기존 GNN 구조들을 압도하였다.

2 3

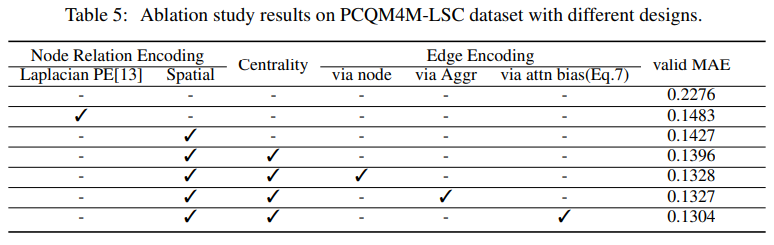
4.1 Ablation Study

해당 방법이 제시한 여러 테크닉 (special bias, positional encoding) 에 대한 ablation 도 모두, performance increament에 적절히 관여 되었다는 것을 보여준다.

4

5. Conclusion

Transformer는 딥러닝 모델로써 사실상 가장 좋은 성능을 거둔다는 느낌을 준다. Transformer 를 어떤 방식으로 응용할지가 현대 딥러닝 연구의 핵심이라고 해도 과언이 아니라는 결론을 얻을 수 있다.

Author Information

  • Minsu Kim
    • KAIST
    • SILAB in Industrial and System Engineering