Write your comments

1. Motivation

제목에서 알 수 있듯, 본 논문의 목적은 Multivariate time series (MTS) data, 즉 여러개의 chanel에서 (ex. 센서) 발생하는 시계열 데이터의 이상치 탐지를 위한 모델을 제시하는 것 입니다. 저자들이 제시 하는 MTS에서의 이상치 탐지의 어려움 3가지는 다음과 같습니다.

1. MTS에서의 이상치는 시간적 (time series의 특성) 그리고 관계적 (multivariate의 특성) 변화 양쪽에 의해 모두 영향을 받음.
2. 여러 chanel 중 몇몇은 noisy time series 일 가능성이 매우 높음.
3. MTS 데이터에는 deterministic 하지 않고 stochastic 한 움직임이 존재.

이러한 어려움을 해결하기 위해 저자가 제시하는 해결 방법은 다음과 같습니다.

1. Reccurent 구조와 Graph 구조를 모두 가지고 있는 모델을 이용.
2. Hierarchical 구조를 이용하여 nosiy time series에 대한 강건성 (robustness)를 제고.
3. Probabilistic 모델링을 통해 stochastic한 움직임을 고려.

저자들은 위 3가지 해결 방안을 모두 통합한 모델로서 Deep Variational Graph Convolutional Recurrent Network (DVGCRN)을 제시합니다. 해당 모델은 Deep Embedding-guided Probabilistic generative Network (DEPN)과 Stacked Graph Convolutional Recurrent Network (SGCRN)으로 이루어져 있는데, 여기서 EPN과 GCRN은 각각 3번과 1번 해결 방안을 맡고 있으며 Deep과 Stacked는 Hierarchical 구조를 의미합니다.

2. Proposed model

2.1 Problem definition

본격적으로 해당 모델에 대해 이야기하기 전에 풀고자 하는 문제를 정확히 정의하도록 하겠습니다. 먼저 n번째 다변량 시계열(n-th MTS)를

\[x_n = \{x_{1,n},x_{2,n},...,x_{T,n}\} \in \mathbb{R}^{T \times V}, \ \text{where} \ n = 1,...,N\]

으로 정의합니다. 여기서 N는 관측치의 수, T는 각 관측치의 time duration, 마지막으로 V는 chanel의 수를 의미합니다.

이제 MTS에서의 이상치 탐지는 주어진 데이터를 바탕으로 특정 시간과 특정 chanel에서의 관측치가 abnormal 한지를 판단하는 문제로 볼 수 정의할 수 있습니다.

2.2 Chanel embedding

MTS의 가장 큰 특징은 여러개의 chanel에서 시계열 데이터가 생성되고 그 chanel들은 서로 관계를 맺고 있다는 것입니다. 본 논문에서는 각 chanel의 특성을 embedding vector

\[\boldsymbol{\alpha}_i^{(0)} \in \mathbb{R}^{d}, i \in \{1,2,...,V\} \ \text{and} \ \boldsymbol{\alpha}^{(0)} = [\boldsymbol{\alpha}_i^{(0)},...,\boldsymbol{\alpha}_V^{(0)}],\]

를 통해 표현합니다. 이제 각 chanel이 d-dimension vector로 표현되기 때문에 chanel 사이의 관계는 embedding vector 간의 inner product를 통해 계산할 수 있습니다. 또한, 최종 모델은 deep (stacked) 모델, 즉 layer가 여러개인 모델이기 때문에 layer-wise embedding

\[\boldsymbol{\alpha}_i^{(l)} \in \mathbb{R}^{d}, l \in {1,...,L} \ \text{where} \ L: \text{number of layers},\]

을 생각할 수 있습니다.

이러한 chanel embedding은 parameter로서 학습되는 것이며, chanel간의 stochastic한 관계를 모델링하기 위해

\[\boldsymbol{\alpha}_i^{(l)} = \mathcal{N}(\hat{\boldsymbol{\mu}}_i^{l},\text{diag}(\hat{\boldsymbol{\sigma}}_i^{(l)})),\]

즉 Gaussian distributed vector로 설정합니다. 이러한 chanel embedding은 이후 설명할 EPN, GCRN module 모두에서 사용됩니다.

2.3 Variational Graph Convolutional Recurrent Network

최종 모델인 DVGCRN을 다루기 전에 layer 개수가 하나인 VGCRN을 기준으로 모델을 설명하도록 하겠습니다. DVGCRN은 Motivation 섹션에서 언급한 robustness를 위해 VGCRN을 여러개 stack 한 것으로 VGCRN의 구조를 이해한다면 그 일반화로 이해할 수 있습니다.

이전에 말씀드렸다시피 VGCRN은 ENP과 GCRN으로 구성되어있기 때문에 각각에 대해 따로 설명하도록 하겠습니다.

2.3.1 Embedding-guided Probablisitic generative Network

EPN은 probabilistic generative model로 다음과 같은 generation process를 가지고 있습니다.

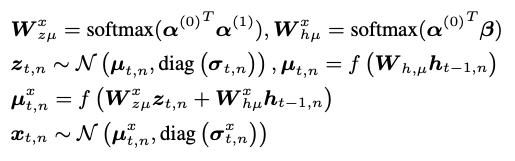
여기서

\[\boldsymbol{z}_{t,n} \in \mathbb{R}^{K}\]

은 Gaussian distributed probabilistic latent variable 이며,

\[\boldsymbol{h}_{t,n} \in \mathbb{R}^{K'}, \ \boldsymbol{\beta} \in \mathbb{R}^{d \times K'}\]

는 각각 시계열적 특성을 반영하기 위해 GCRN에서 가져온 deterministic latent state 그리고 latent state를 embedding space로 mapping 하기 위한 행렬입니다.

최종적으로 EPN은 probabilistic generative process에 chanel embedding을 사용함으로서 여러 chanel들 간의 복잡한 관계를 고려하면서 latent space를 학습할 수 있습니다. 또한, GCRN에서 가져온 deterministic latent state를 통해 시계열적인 특성까지 반영한 generation이 가능합니다.

2.3.2 Graph Convolutional Recurrent Network

GCRN은 chanel 간의 inter-dependence를 추론하기 위해 data adaptive graph convolutional generation module을 먼저 사용합니다. 해당 module은 다음과 같은 형태를 가지고 있는데,

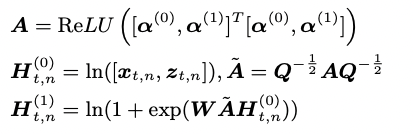
chanel embedding과 EPN에서 추론한 latent vector가 사용됨을 알 수 있습니다. 여기서 A를 symmetric한 adjacent matrix로 생각할 수 있고 (degree matrix Q를 이용해 normalized), W는 GCN filter를 의미합니다. 또한, temporal correlation을 발견하기 위해 GCN에 reccurent 구조,

\[\boldsymbol{h}_{t,n} = f_{\theta}(\boldsymbol{H}_{t,n}^{(1)},\boldsymbol{h}_{t-1,n})\]

를 도입힙나다. 여기서 함수 f는 non-linear transition function으로 LSTM을 통해 구현할 수 있습니다. 최종적으로 GCRN은 chanel간의 dependency와 temporal correlation을 고려함과 동시에 EPN의 latent vector를 사용함으로서 probabilistic한 특성까지 가질 수 있게 되었습니다.

2.4 Deep Variational Graph Convolutional Reccurent Network

DVGCRN은 모델의 robustness를 위해 VGCRN에 layer를 겹겹이 쌓은 것으로 VGCRN의 일반화로 이해할 수 있습니다. VGCRN이 geneartion module EPN과 spatio-temporal module GCRN으로 이루어져 있기 때문에, 각각의 모듈에 대한 일반화인 Deep EPN과 Stacked GCRN으로 DVGCRN을 구성합니다.

먼저, DEPN은 다음과 같은 구조를 가지고 있으며

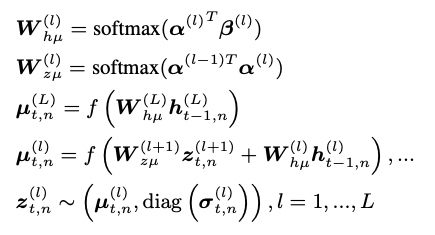
SGCRN 역시 layer 단위의

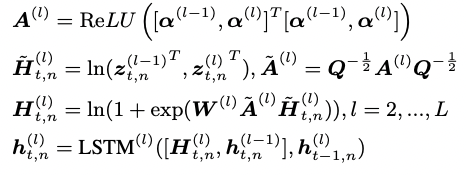
구조를 가지고 있습니다. 각 역할은 EPN과 GCRN과 동일하기 때문에 자세한 설명은 생략하도록 하겠습니다.

다만, hierarchical structure로 인해 고차원 layer에서 stochastic한 잠재변수가 prior distribution으로 collapse 하는 경우가 발생할 수 있습니다. 이를 막기 위해 deterministic-upward path 뿐만 아니라 input에서 direct하게 multi-layer latent representation으로 이어지는 다음과 같은 mapping을 이용합니다:

\[\hat{\mathbf{\mu}}_{t,n}^{(l)} = f(\mathbf{C}^{(l)}_{x \mu} \mathbf{x}_{t,n} + \mathbf{C}^{(l)}_{h \mu}\mathbf{h}_{t-1,n}) \ \text{and} \ \hat{\mathbf{\sigma}}_{t,n}^{(l)} = f(\mathbf{C}^{(l)}_{x \sigma} \mathbf{x}_{t,n} + \mathbf{C}^{(l)}_{h\sigma}\mathbf{h}_{t-1,n}).\]

여기서 C로 표시된 matrix들은 모두 학습가능한 parameter입니다. 이제, latent feature와 stochastic-downward path를 통해 구한 prior를 함께 이용하여 latent space의 variational posterior를 구합니다:

\[q(\mathbf{z}_{t,n}^{(l)}) = \mathcal{N}(\mathbf{\mu}^{(l)}_{t,n}, \text{diag}(\mathbf{\sigma}^{(l)}_{t,n})),\]

where

\[\mathbf{\mu}^{(l)}_{t,n} = \text{linear}(\hat{\mathbf{\mu}}_{t,n}^{(l)} + \mathbf{W}^{(l)}_{z \mu} \mathbf{z}^{(l+1)}_{t,n}) \ \text{and} \ \mathbf{\sigma}^{(l)}_{t,n} = \text{Softplus}(\text{linear}(\hat{\mathbf{\sigma}}_{t,n}^{(l)} + 1)).\]

최종적으로 DVGCRN을 도식화하면 다음과 같이 나타낼 수 있습니다.

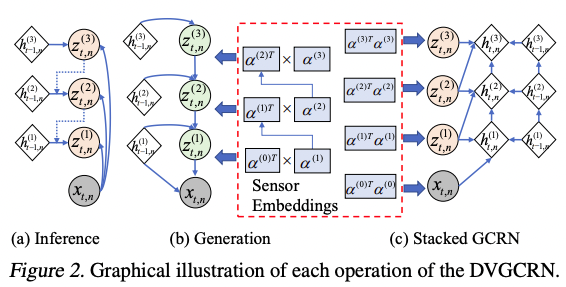
DVGCRN 모델은 이름에서 알 수 있듯, variational inference를 통해 학습을 진행합니다 (ELBO 사용). 또한, generative model인 DEPN과 recurrent model인 SGCRN을 module로 사용하고 있기 때문에 각각 reconstruction loss과 forecasting loss를 combine 하여 loss function을 구성합니다. 최종적으로 ELBO는 다음과 같은 형태를 띄게 되는데,

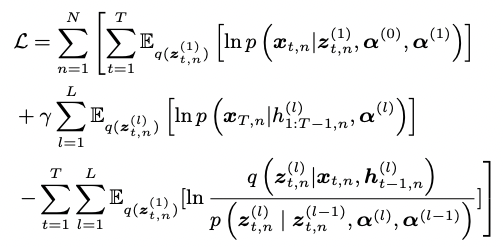
첫번째 term은 reconstruction loss, 두번째 term은 forecasting loss 그리고 마지막 term은 KL-Divergence로 이해할 수 있습니다. 두번째 term을 보면 앞에 hyperparameter를 통해 reconstruction loss와 forecasting loss 사이의 balance를 조절할 수 있음을 알 수 있습니다.

3. Anomaly detection based on DVGCRN

DVGCRN의 목적은 MTS 데이터의 unsupervised anomaly detection입니다. 이를 위해 다른 abnomaly detection 모델들과 유사하게, reconstruction probability와 prediction error를 합친 anomaly score를 이용하여 일정 threshold를 넘기면 abnormal로 판단합니다.

\[S_{t,n} = (S_{t,n}^r + \gamma(-S_{t,n}^p))/(1+\gamma) \ \text{where} \ \\ S_{t,n}^r = \text{log} \ p(\boldsymbol{x}_{t,n}|\boldsymbol{z}_{t,n}), \ S_{t,n}^{p} = (\boldsymbol{x}_{t,n} - \hat{\boldsymbol{x}}_{t,n})^2\]

이때, multi-layer representation을 더 적극적으로 활용하기 위해 reconstruction score를 united conditional probability

\[\begin{aligned} \hat{S}_{t,n}^r &= \cfrac{1}{L} \text{log} \ p \big(\boldsymbol{x}_{t,n}, \boldsymbol{z}_{t,n}^{(1)},...,\boldsymbol{z}_{t,n}^{(L-1)}| \boldsymbol{z}_{t,n}^{(L)} \big) \\ &= \cfrac{1}{L}(\text{log} \ p(\boldsymbol{x}_{t,n}|\boldsymbol{z}_{t,n}^{(1)})+ \sum_{l = 1}^{L-1} \text{log} \ p (\boldsymbol{z}_{t,n}^{l}|\boldsymbol{z}_{t,n}^{l+1})) \end{aligned}\]

로 사용할 수도 있습니다.

마지막으로 threshold의 경우 Peaks-Over-Threhold (POT) (Siffer et al., 2017)를 통해 구합니다. DVGCRN을 이용한 MST의 anomaly detection을 도식화 하면 다음과 같이 그릴 수 있습니다.

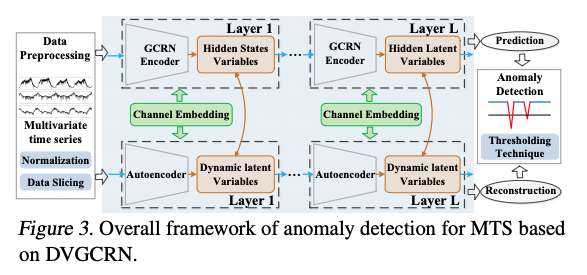
# 4. Empricial results

마지막으로 본 논문은 실제 multivariate KPI 데이터인 DND와 public data 3개 (MD,MSL,SMAP)를 이용한 experiment 결과를 제시합니다. (각 data에는 ground-truth anomaly가 알려져 있음) 데이터에 대한 자세한 설명은 원문에 자세하게 나와있으니 리뷰에서는 따로 다루지 않겠습니다.

4.1 Quantitative comparison

먼저 quantitative comparison 입니다. quantitative comparison에 쓰인 metric은 Precision, Recall 그리고 F1 score 입니다.

다음 그림은 DVGCRN의 hyperparameter 설정에 따른 score의 변화와 ablation study입니다.

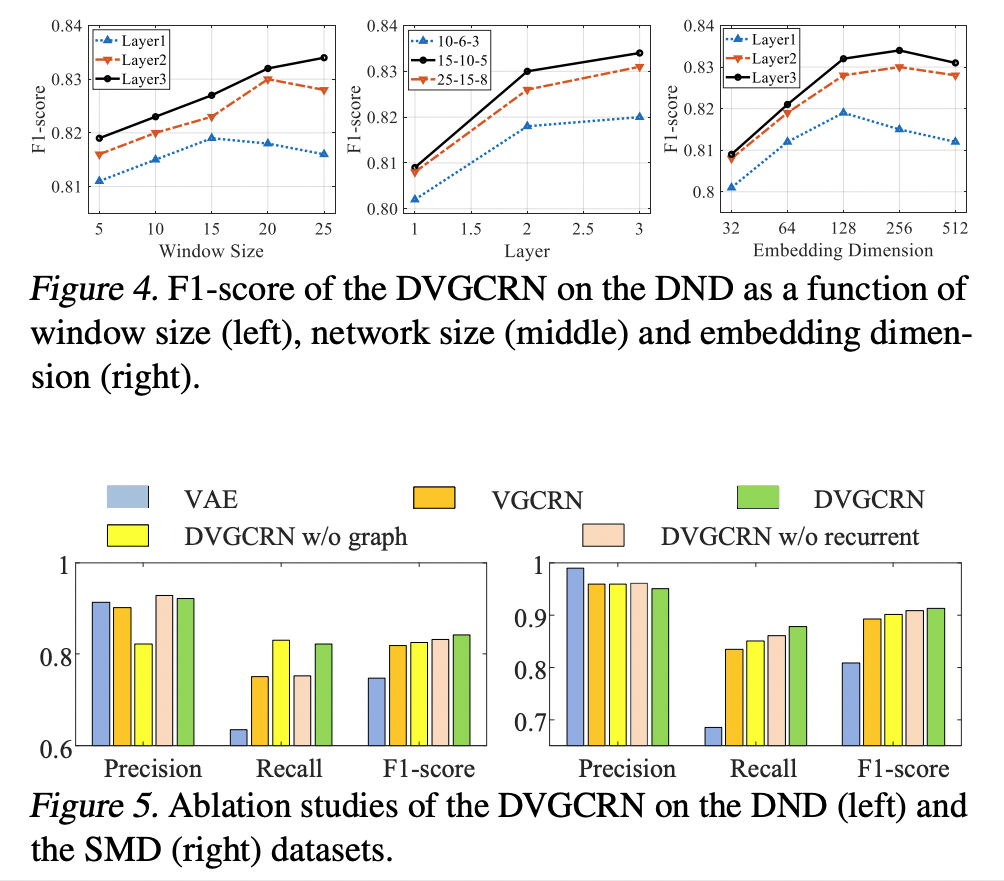
3-layer 모델에서 window size(T)가 클수록 성능이 개선 되는 것(왼쪽 그림)과 network의 사이즈와 무관하게 layer의 수가 클 수록 좋은 성능을 보이는 것(중간 그림)을 통해 deep network가 좋은 성능을 보이고 있음을 알 수 있습니다. 다만, embedding dimension의 경우 layer의 개수와 무관하게 너무 큰 값의 경우 성능이 하락하는 모습을 보이고 있습니다.

Ablation study를 통해서는 graph와 recurrent 구조 모두 DVGCRN의 성능에 중요한 영향을 끼치고 있다는 것을 알 수 있습니다.

다음 표는 여러 baseline method들과 DVGCRN을 비교한 결과입니다.

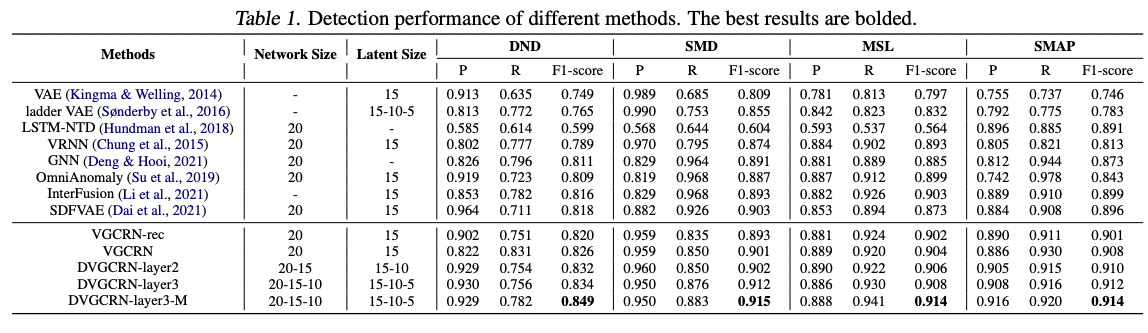
해당 표를 통해 모든 dataset에서 F1 score를 기준으로 proposed method들이 다른 baseline 모델들에 비해 훨씬 좋은 성능을 보이는 것을 확인할 수 있습니다. 이를 통해 MST의 stochastic 한 특성을 잡아냄과 동시에 chanel dependency를 고려하는 본 논문의 framework가 성공했음을 알 수 있습니다.

Proposed method 내에서는

1. VGCRN-rec의 경우 loss function에 reconstruction loss만 사용하여 학습한 경우인데, 가장 낮은 성능을 보이는 것으로 보아 loss function에 forecasting loss를 추가한 것이 옳은 방향이었음을 알 수 있습니다.
2. 또한, VGCRN에 비해 DVGCRN이 우월한 성능을 보여 hierarchical structure를 도입한 것이 실제로 robustness에 도움을 줬음을 확인할 수 있습니다.
3. 마지막으로 DVGCRN-M 모델은 section 3에서 언급한 united conditional probability를 reconstruction loss로 사용한 모델인데, 역시 가장 좋은 성능을 보여 해당 loss를 사용 하는 것이 학습에 도움이 되었음을 알 수 있습니다.

4.2 Qulitative comparison

다음으로는 실제 anomaly socre의 시각화를 통해 qualitative comparison을 진행합니다.

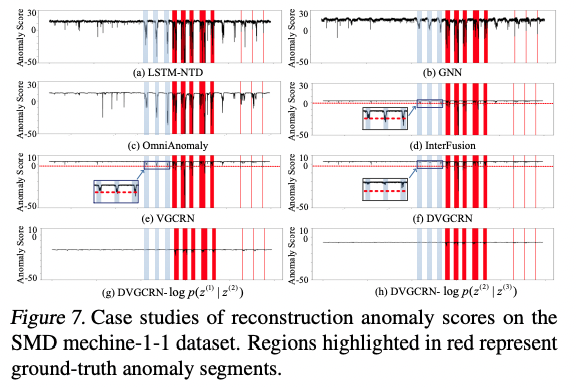
Deterministic model인 LSTM-NTD 그리고 GNN의 경우 MTS의 stochastic property를 고려하지 않아 anomaly score가 굉장히 불안정한 모습을 확인할 수 있고, 다른 probabilistic model들인 Interfusion과 Omni Anomaly와 비교해봐도 MTS의 3가지 특성을 모두 고려한 VGCRN과 DVGCRN이 더욱 매끄럽고 안정적으로 anomaly를 찾아내는 것을 확인할 수 있습니다. 이는 quantitative comparison에서 보았던 결과와 일맥상통하는 모습으로 생각할 수 있습니다.

또한, latent spcae의 log-likelihood를 시각화 해보아도 normal situation에서는 안정적인 모습을 보이다가 anormaly segment에서 불안정한 모습을 확인할 수 있는데, 이는 multi-layer structure의 채택이 좋은 전략임을 보이고 있습니다.

5. Conclusion

본 논문은 Multivariate Time Series의 3가지 특성

1. Temporal and chanel dependency
2. Existence of noisy chanels
3. Stochasticity

을 모두 고려한 Deep Variational Graph Convolutional Recurrent Network와 그 학습 방법을 제시합니다. 그리고, 실제 데이터를 이용한 quantitative comparison과 qualitative comparison을 통해 기존의 baseline 모델들에 비해 MTS의 unsupervised anomaly detection에 우수한 성능을 보임을 증명합니다.