1. Problem Definition

시계열분석의 전형적인 문제 중 하나로서, 교통의 흐름 예측(Traffic Flow Forecasting) 은 머신러닝의 가장 중요한 응용 분야 중 하나이자, Urban Science 분야에서 풀어야 할 숙제 중 하나입니다.
최근 도시 인구 집중 현상 등으로 인해 우리나라 내 주요 도시를 가보면 도로가 차로 가득한 것을 쉽게 볼 수 있습니다. 이렇게 도로 네트워크 내의 차량 수가 증가하면 교통 관리 시스템의 역할이 매우 중요해지는데요. 특히 다변화되고 복잡해지는 도로 교통망에서의 효율적인 교통 관리를 위해서는 지능형 교통 시스템(Intelligent Transportation Systems; ITS) 이 필요한데, 이때 교통 흐름을 정확히 예측할수록 ITS의 성능이 높아집니다. 그러므로 우리는 교통 흐름을 정확히 예측하는 Traffic Forecasting 알고리즘이 필요합니다.

그러나 도로 네크워크는 복잡한 시공간 의존성을 동적으로 가진다는 점 에서 교통 흐름을 예측하는 것이 꽤나 어려운 일인데요. 이러한 도로 네트워크는 몇 가지 특징이 있습니다.
먼저 도로 네트워크는 Node와 Link들 간의 조합인 Graph 구조로 표현 된다는 특징입니다. Graph 구조는 다른 Tabular data, Image data 등 일반적인 유클리디안 구조의 데이터와 다르게 비 유클리디안(Non-Euclidean) 구조의 데이터라는 점에서 이러한 특징을 효과적으로 고려한 모델이 필요합니다. 그리고 시간적인 요소와 공간적인 요소가 상호 의존적인 관계를 가진다는 특징을 고려하여 이를 동시에 고려할 수 있는 모델을 설계해야 합니다.

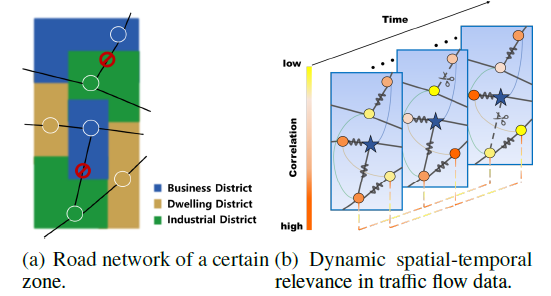
[Figure 1. Dynamic spatial-temporal correlations in real world traffic data]

위 Figure의 (a)에서 각 colored zone은 district의 목적에 따라 색깔로 구분한 것이고, 검은 직선은 실제 도로이며, district 위의 원은 노드를 의미합니다. 결과적으로 도로 네트워크를 가시적으로 표현한 것입니다. 그리고 (b)는 (a)의 도로 네트워크의 시공간 요소의 상호 의존적인 패턴을 동적으로 나타낸 것입니다. 여기서 시간의 흐름에 따라 동적인 요소의 변화를 파악하는 것이 왜 중요할까요?

직관적으로 생각했을 때 도로 네트워크 내 요소들은 여러가지 무작위 요인에 의해 영향을 받곤 합니다. 예를 들어 카이스트 내 서측 카이대로가 어제까진 멀쩡했으나, 오늘 갑자기 도로 보수를 할 수도 있고, 카이스트 정문 앞 삼거리에서 오늘 아침에 사고가 발생해서 예상치 못한 교통 체증이 발생할 수도 있습니다. 이러한 무작위 요인들은 인접 노드 간의 도착 시간 간격에 영향을 미치는 요소가 될 수 있습니다. 또한 기존의 3차선 도로가 도로 확장 공사로 인해 4차선 도로가 되면, 과거에는 정체가 되었던 구간이 미래에는 정체가 발생하지 않는 평범한 도로가 될 수 있겠죠.

반면에 (a)처럼 유사한 기능을 갖는 District(ex. business, industrial, etc) 는 각 District 간의 거리가 떨어져있어도 기능이 유사하다면 비슷한 패턴 을 보입니다. 예를 들어 매일 출근 시간에는 사무실이 밀집된 Business District 지역이 동시에 혼잡해집니다. 여의도와 강남은 서로 물리적으로 떨어져있지만, 아침 7시부터 9시 사이에 동일하게 차로 붐비는 것을 예시로 들 수 있겠습니다. Business District라는 유사한 기능 을 갖고 있기 때문이죠.

이처럼 각 노드에서의 교통 네트워크는 매우 동적이고 복잡한 시공간 요소의 상호 의존적인 패턴 을 보입니다. 그러므로 우리는 Graph 구조를 고려한 효과적인 모델을 설계해 시공간의 상호 의존적인 관계를 포착할 수 있으면서, 동적인 요소를 동시에 고려하는 모델을 구상해야 합니다.

2. Motivation

이를 위해서 여러 아이디어들이 등장했습니다.

시공간적 요소를 동시에 고려하는 고전적인 방법 중 하나는 합성곱 신경망(CNN)과 순환 신경망(RNN)을 연결하는 모델을 구축 하는 것입니다. (Zhang et al., 2016; Li & Shahabi, 2018)

특히 CNN은 지역적인 공간 상관관계를 포착하는 데 적합하지만, Graph 구조인 도로 네트워크의 특징을 잡아내는 데 적합하진 않습니다. 그렇다면 GCN(Graph Convolution Network) 은 어떨까요? GCN은 비유클리디안 공간인 Graph 구조의 특징을 잘 잡아낼 수 있는 좋은 모델이라는 점에서 도로 네트워크에 적합한 모델입니다. (Li et al., 2017; Yu et al., 2017; Zhao et al., 2019)

그럼에도 불구하고 대부분의 기존 GCN 모델은 동적인 관계를 잡아내기엔 어려움이 있습니다. 왜냐하면 기존 GCN 모델들은 미리 정의된 Static adjacency matrix 를 사용해서 Spatial correlation을 모델에 반영하기 때문에 도로 네트워크 내의 Spatial dependency의 동적인 변화를 잡아내기에 한계가 있습니다.

즉 Adjacency matrix는 그래프 구조에서 단순히 이웃 노드와의 연결 여부에 따라 1 혹은 0으로 연결 관계를 나타내는데, 연결된 노드 중에서도 더 중요한 노드가 있고 그렇지 않은 노드가 있음에도 불구하고 Static Adjacency Matrix는 이러한 관계를 포착하는 데 어려움이 있다는 것입니다.

Time Series Data의 similarity를 포착하기 위해 Dynamic Time Warping(DTW) 의 개념 (Berndt & Clifford, 1994) 을 이용해서 GCN에 반영한 SFTGCN 라는 모델도 등장했었으나, 이는 데이터 시퀀스 자체의 similarity만 포착한다는 점에서 semantic relevance를 고려하기엔 한계가 있습니다. (Li & Zhu, 2021)

이처럼 Time Series Traffic Data는 다음과 같은 특징이 있는데요. Dynamic similar pattern과 Random irregular pattern이라고 하겠습니다.

직관적으로 생각해보면 차가 붐비는 대부분의 도로는 요일별로 명확한 패턴이 구분됩니다. 단순히 이번 한 주만 보는 게 아닌, 한달 간의 데이터, 혹은 1년 이상의 데이터를 고려하는 경우를 생각해보죠.

카이스트 앞 삼거리는 출근 시간대, 혹은 퇴근 시간대만 되면 항상 붐빕니다. 이는 관찰한 기간에 상관없이 패턴이 유사함을 알 수 있습니다. 즉 이 시간대를 제외하고는 낮 시간대, 혹은 주말의 경우엔 차가 거의 없다는 것이죠.

그러나 우리가 예측하지 못하는 이벤트들이 간혹 발생할 수 있습니다. 때로는 학교 앞 삼거리에서 도로 보수공사로 인해 특정 차로가 통행이 제한되면 예상치 못하게 차가 막히지 않는 시간대임에도 차가 막힐 수도 있고, 평일임에도 개교기념일로 인해 학교 교직원들이 출근을 하지 않는다면 출퇴근 시간대에도 차가 막히지 않을 수 있겠죠.

도로의 보수 공사같은 불규칙한 이벤트들은 short-term이든 long-term이든 irregular pattern이겠지만, 개교기념일은 과거부터 쭉 관측했을 때 long-term에서는 분명 pattern이 있을 겁니다. 즉 우리는 short-term과 long-term 모두 temporal correlation을 동시에 고려할 필요가 있습니다.

이를 위해 본 논문에서는 다른 연구에서 사용한 Pre-trained static adjacency matrix를 사용하지 않고, 장기간의 time-series data로부터 노드 간의 spatial association의 동적인 속성을 고려한 모델을 설명했습니다.

바로 Dynamic Spatial-Temporal Aware Graph Neural Network(DSTAGNN) 이라는 모델입니다.

다른 모델들과 차별화되는 점은 서두에 계속 강조되었던 ‘동적인 관계’를 포착하기 위해 노력했다는 점에서 흥미로운 연구라고 할 수 있겠습니다.

3. Preliminary

본격적으로 설명하기에 앞서, 두 가지 사항을 짚고 넘어가겠습니다.

논문에서 사용된 주요 Notation과, 논문에서 제안한 아키텍처를 이해하기 위한 주요 개념들에 대해 다루겠습니다.

3.1 Notation

Graph $G = (V, E)$, $V$ : a set of N nodes, $E$ : a set of Edges
$A \in \mathbb{R}^{N \times N}$ : Adjacency Matrix ( $A_{ij} = 1 \,\; if \;\; v_i, v_j \in V \; and \; (v_i, v_j) \in E$ )
$X^t \in \mathbb{R}^{N \times C_p}$ : Traffic Status(Graph Signal) i.e. Traffic volume, speed
$X^{(t-M+1):t} \in \mathbb{R}^{N \times 1 \times M}$ : Recorded Data(t-M+1시점부터 t 시점 까지의 M 기간의 데이터)
$X^{(t+1):(t+T)} \in \mathbb{R}^{N \times 1 \times T}$ : Data predicted for T time steps
$\mathcal{F}$ : Model to predict for T time steps
$X^{(t+1):(t+T)} = \mathcal{F}[X^{(t-M+1):t}\; ; \,G]$ : Model $\mathcal{F}$를 이용해 과거 데이터로 미래 데이터를 예측
$W\,[u, v] = \inf\limits_{\gamma \in \Pi_{[u, v]}} \int_{x}\int_{y} \gamma(x,y)d(x,y) \, dxdy$ : Wasserstein Distance
- s.t. $\int \gamma(x,y)dy = u(x)$ and $\int \gamma(x,y)dx = v(y)$ : Marginal Distribution
- $\gamma(x,y)$ : Joint Distribution $\Pi[u,v]$
- $d(x,y)$ : cost of moving the unit mass from $x$ to $y$

3.2 Conceptual Background

이 챕터에서는 본격적인 아키텍처에 대해 다루기 전에, 이해를 돕고자 아키텍처와 관련된 기본 개념들에 대해 소개하고자 합니다.

3.2.1 Graph Convolution

Graph Convolution Networks(GCN)

Graph Convolution Networks(GCN)은 그래프 구조 데이터를 처리하기 위해 설계된 신경망 아키텍처 중 하나입니다. 전통적인 Neural Network나 Convolution Neural Networks(CNN)이 유클리드 데이터(Ex. Tabular Data, Image, Text 등)를 처리하는 데 특화되어 있는 아키텍처라면, 노드(Node)와 노드들 사이의 연결 관계를 나타내는 엣지(Edge)로 구성되는 비유클리드 데이터인 그래프 구조 데이터를 효율적으로 다루기 위해 GNN을 사용합니다.

GNN 중 GCN(Graph Convolution Networks)은 합성곱 신경망의 아이디어를 빌려서 그래프 상의 노드들을 주변 노드의 정보를 통합하여 새로운 특성 공간으로 매핑 하는 것입니다. 즉 이미지 데이터에서 합성곱 신경망을 적용하는 프로세스를 예로 들면, 한 픽셀로부터 주변 픽셀의 정보를 이용해 합성곱 연산을 수행하는 것처럼, 그래프 구조에서는 한 노드로부터 주변 노드의 정보를 통합해 연산한다는 점에서 기존 CNN과 유사한 역할을 합니다.

GCN에서 합성곱 연산은 각 노드가 주변 이웃 노드들의 특성 정보를 수집하고 통합하는 과정으로 이루어집니다. 이때 노드의 특성 정보와 그래프의 구조 정보를 모두 반영하여 각 노드에 대한 새로운 특성 표현을 생성합니다. 그 순서는 다음과 같습니다.

(1) 이웃 수집 : 각 노드는 자신과 연결된 이웃 노드들의 특성을 수집합니다.

(2) 통합 및 변환 : 수집된 이웃 노드들의 특성과 자신의 특성을 통합합니다. 이때 그래프의 노드들 사이의 연결 관계를 나타내는 인접 행렬(Adjacency Matrix)을 이용합니다.

(3) 비선형 활성화 : 변환된 특성에 대해 비선형 활성화 함수를 적용합니다.

이를 수식으로 표현하면 다음과 같습니다.

$H^{(l+1)} = \sigma(\hat{A}H^{(l)}W^{(l)})$
- $H^{(l)}$ : $l$번째 층에서 노드 특성 행렬
- $W^{(l)}$ : $l$번째 층에서 가중치 행렬
- $\hat{A}$ : 정규화된 인접 행렬
- $\sigma$ : 비선형 활성화 함수(ex. ReLU)
[Figure 2. The Architecture of GCN]
Chebyshev-Polynomial Expansion

체비셰프 다항식(Chebyshev Polynomials)은 삼각 함수의 항등식에서 등장하는 직교 다항식열로, Chebyshev Polynomial Expansion은 이러한 체비셰프 다항식을 이용해서 복잡한 함수를 주어진 범위 내에서 다항식의 형태로 함수를 근사하는 데 사용되는 방법론입니다.
특히 그래프 신호 처리에서는 그래프 라플라시안의 고유값(Eigenvalue)을 기반으로 한 스펙트럼 필터를 체비셰프 다항식으로 근사화하여 효율적인 계산을 가능하게 합니다.

GCN은 크게 Spectral-type GCN과 Spatial-type GCN으로 구분되는데, 이중 스펙트럼 그래프 컨볼루션은 그래프의 구조적 정보를 처리하기 위해 그래프 라플라시안의 스펙트럼 분석을 활용합니다. 다시 말해서 스펙트럼 그래프 컨볼루션은 그래프 라플라시안의 고유벡터를 사용해서 정의되는데, 이는 전체 그래프에 대한 고유값 분해(Eigen Decomposion)를 필요로 합니다. 하지만 고유값 분해는 계산 비용이 매우 큰 작업입니다.

이 문제를 해결하기 위해 Chebyshev Polynomial Expansion이 사용됩니다. 이는 고유값 분해 없이 스펙트럼 필터를 근사할 수 있게 해줌으로써 대규모 그래프에서도 효율적으로 GCN을 수행할 수 있게 합니다.
구체적으로 스펙트럼 필터를 체비셰프 다항식의 선형 조합으로 근사하고, 이를 그래프 라플라시안에 적용함으로써 노드의 이웃 정보를 효과적으로 추출할 수 있습니다.
Graph Attention Networks(GAT)

그래프 어텐션(GAT)는 그래프 구조 데이터를 처리하기 위해 설계된 신경망 아키텍처로, Attention 매커니즘을 사용하여 그래프의 노드 간 상호작용을 모델링합니다.
Attention에서 핵심적으로 쓰인 아이디어가 ‘더 중요한 정보에 가중치를 두자’였던 것에 기반해서 GAT 또한 한 노드로부터 연결된 모든 이웃 노드의 정보를 동일한 기여도로 받아들이는 게 아닌 특정 상황에서 더 중요한 이웃 노드의 정보에 더 많은 가중치를 두어 정보를 통합합니다.

직관적으로 생각해서 도로 네트워크에서도 A 노드(교차로)로부터 4개의 도로가 연결돼있는 사거리인 상황을 가정할 때, 모든 도로가 동일한 교통량을 갖고 A 노드를 통과하는 게 아니라 좀 더 유동인구가 많은 지역으로부터 오는 도로가 교통 체증을 유발하는 데 더 크게 기여하는 상황을 생각해보면 GAT의 접근이 합리적임을 이해하실 수 있을 거라 생각합니다.

GAT는 다음과 같은 과정을 통해 그래프 데이터의 구조적 특성과 노드 간의 관계를 더 잘 반영할 수 있게 해줍니다.

(1) 어텐션 계수 계산 : GAT는 먼저 각 노드 쌍에 대해 어텐션 계수를 계산합니다. 이 계수는 해당 이웃 노드가 현재 노드의 새로운 특성 표현을 생성하는 데 얼마나 중요한지를 나타냅니다. 어텐션 계수는 노드의 현재 특성과 가중치를 사용하여 계산되며, softmax 함수를 통해 정규화됩니다.

(2) 가중 특성 통합 : 계산된 어텐션 계수를 사용하여, 각 노드는 이웃 노드들의 특성을 가중평균하여 자신의 새로운 특성 표현을 생성합니다. 이 과정에서 중요도가 높은 이웃 노드의 특성이 더 큰 영향을 미치게 됩니다.

(3) Multi-Head Attention : 다중 어텐션 헤드(Multi-Head Attention)를 사용하여 정보를 수집함으로써 모델의 복잡도와 표현력을 증가시킵니다. 다중 어텐션 헤드에서 각 어텐션 헤드는 독립적으로 이웃 노드로부터 정보를 수집하고, 최종적으로 이들의 출력을 결합하여 노드의 새로운 특성 표현을 생성합니다.

3.2.2 Measuring Differences in Probability Distributions

Dynamic Spatial Dependency in Road Networks

도로 네트워크에서 노드 간 Dynamic Spatial Dependency(동적 공간 의존성) 을 식별하는 과정은 도로 네트워크 내의 각 노드 간의 상호작용과 연결성의 변화를 이해하는 데 중요한 과정입니다.
도로는 시간에 따라 변합니다. 특정 지점에서 예상치 못하게 도로 공사를 하거나, 사고가 발생해서 교통량의 영향을 주는 경우, 다른 인접 노드의 교통량까지 영향을 주는 연쇄 효과가 발생하기 때문입니다. 그리고 이러한 이벤트들은 시간에 따라 발생하는 경우도 있고 발생하지 않는 경우도 있으며, 시간에 따라 서로 영향을 주는 노드 또한 달라지게 됩니다. 그러므로 Spatial Dependency는 정적이 아닌 동적인 요소로 간주하고, 이를 동적으로 모델링해야 합니다.

이러한 의존성을 모델링하기 위해, 각 노드에서 관찰된 데이터를 바탕으로 확률 분포를 생성하고, 이 확률 분포들 간의 거리를 계산하는 방법론을 사용할 수 있습니다. 예를 들어 특정 시간 동안 해당 노드를 통과하는 차량 수의 분포를 확률분포로 나타내는 경우를 떠올려보면 되겠습니다.

두 노드의 확률 분포가 주어지면, 이 두 분포 간의 거리(차이)를 계산하여 노드들 사이의 관계를 정량화할 수 있습니다. 직관적으로 생각했을 때 두 노드가 비슷하다는 것은 두 노드의 확률분포가 유사하다는 것 으로 이해할 수 있겠죠. 그렇다면 거리를 계산할 때 거리가 작을 것이고요. 그러므로 이러한 거리 측정은 두 노드 간의 상호작용과 연결성의 강도를 정량적으로 평가할 수 있는 매커니즘을 제공한다는 점에서 유용합니다.

확률분포 간의 거리를 계산하는 방법론은 대표적으로 KL-Divergence(Kullback-Leibler Divergence) 가 있는데요. 두 확률분포의 차이를 계산할 때, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피의 차이를 계산하는 방법론입니다. 이 연구에서는 KL-Divergence 대신 Wasserstein Distance 라는 Metric을 사용했습니다.
Wasserstein Distance

Wasserstein Distance(바서슈타인 거리)는 두 확률 분포 사이의 최소 비용으로 확률 질량을 한 분포에서 다른 분포로 이동시키기 위해 필요한 작업, 또는 에너지의 양을 구하는 metric 입니다. 이 개념은 한 지점에서 다른 지점으로 질량(mass)을 옮기는 데 필요한 최소 비용을 계산하는 문제에서 유래했습니다.

공식은 다음과 같습니다.
- $W\,[u, v] = \inf\limits_{\gamma \in \Pi_{[u, v]}} \int_{x}\int_{y} \gamma(x,y)d(x,y) \, dxdy$ : Wasserstein Distance
  - s.t. $\int \gamma(x,y)dy = u(x)$ and $\int \gamma(x,y)dx = v(y)$ : Marginal Distribution
  - $\gamma(x,y)$ : Joint Distribution $\Pi[u,v]$
  - $d(x,y)$ : cost of moving the unit mass from $x$ to $y$
여기서 $u$, $v$는 각각 두 확률공간 $X, Y$ 위의 확률분포이고, $d(x, y)$는 확률공간 내 두 점 $x, y$ 사이의 거리를 나타냅니다.
그리고 $\Pi_{[u, v]}$ 는 두 확률분포 $u, v$의 결합확률분포(Joint Distribution)를 모은 집합이고, $\gamma$는 그 중 하나입니다.

즉 Wasserstein Distance를 다시 쓰면 다음과 같습니다.
- $W\,[u, v] = \inf\limits_{\gamma \in \Pi_{[u, v]}} \mathbb{E}^{\gamma}[d(x,y)] \,$
즉 모든 결합확률분포 중에서 distance $d(x,y)$ 의 기댓값을 가장 작게 추정한 값, 최소 거리를 찾는 연산 이라고 할 수 있습니다.

아래 Figure 2-2를 보시면 직관적으로 이해하실 수 있을 것이라 생각합니다.

[Figure 2-2. Wasserstein Distance]

4. Methodology

이번 챕터에서는 Chapter 3의 내용을 바탕으로 연구에서 제안한 모델의 아키텍처에 대해 다뤄보겠습니다.

Traffic Forecasting은 단순히 Tabular Data를 기반으로 예측하는 것에 중점을 둔 문제가 아닌, 도로 네트워크의 시공간적 요소들 동시에 고려한 예측 문제라는 점에서 시공간 예측(Spatial-Temporal Forecasting) 에 대해 먼저 알아야 합니다.

4.1 Spatial-Temporal Forecasting

: Spatial-Temporal Forecasting은 공간적 및 시간적 데이터를 기반으로 미래의 상태나 패턴을 예측하는 과정입니다. 이러한 종류의 예측은 공간적인 요소와 시간적인 요소가 모두 중요한 역할을 하는 데이터에서 특히 중요합니다.

우리가 본 리뷰에서 다루고 있는 교통 흐름 예측(Traffic Flow Forecasting) 문제 가 대표적인 문제이고, 이뿐만이 아니라 기후 변화, 전염병 확산, 에너지 수요 등 분야들의 데이터 모두 Spatial-Temporal 특성을 갖고 있습니다.

이러한 데이터의 특징은 공간적 의존성(Spatial Dependence), 시간적 의존성(Temporal Dependence)을 갖고 있다는 것 입니다.
공간적 의존성은 특정 위치의 데이터가 주변 위치의 데이터와 상호 연관되어 있는 특성을 의미하고, 시간적 의존성은 현재 시점의 데이터가 과거의 데이터에 의존하는 특성을 말합니다.
공간적 의존성은 위 챕터에서 설명한 도로 네트워크의 교차로 상황을 생각하면 되겠으며, 시간적 의존성은 주식을 예로 들 때, 오늘의 주가는 어제의 주가와 무관하지 않다는 상황을 생각하면 되겠습니다.

또한 시공간적 요소가 상호 의존성을 갖는 경우 또한 존재할 것입니다. 예를 들어 출퇴근 시간에 주요 도로에서 발생하는 정체는 주변 도로로 퍼져나가며, 이러한 패턴은 일일 단위, 혹은 주간, 월간 등 특정 시간 패턴에 따라 반복될 수 있습니다.

GCN에서 이러한 시공간적 요소의 상관관계를 포착하고자 다양한 방법론들이 제시되었습니다. 그래프 구조에서는 공간적 의존성을 포착하는 방법은 바로 인접 행렬(Adjacency Matrix)를 사용하는 것인데요. 대부분 선행연구에서도 인접 행렬을 사용했습니다.

그러나 인접행렬의 한계는 ‘정적인 관계’만을 나타낸다는 것 입니다. 시간의 흐름에 따라 도로가 새로 연결되기도 하고, 끊어졌다가 다시 복구되기도 하고, 다양한 요인에 의해서 연결 여부의 변화가 생기는데, 정적인 인접행렬(Static Adjacency Matrix)은 잠재적인 동적 의존성 정보를 놓칠 수 있습니다.

또한 인접행렬은 단순히 연결되었으면 1, 연결되지 않았으면 0을 부여하는 행렬입니다. 하지만 위에서 attention network에 대해 설명하면서 다뤘듯이, 연결된 이웃 노드들 중에서도 노드마다의 중요한 정도가 상이하므로 연결 여부로만 공간적 의존성을 모델링하는 것은 적절하지 않습니다.

그러므로 이 연구에서는 시간의 흐름에 따라 변하는 동적인 관계를 모델링하면서도, 시공간적 의존성을 잘 나타낼 수 있는 아키텍처를 제시해야 한다고 주장합니다.
즉 Dynamic Spatial-Temporal Dependency 를 잘 나타낼 수 있는 모델이 바로 Dynamic Spatial-Temporal Aware Graph Neural Networks(DSTAGNN) 입니다.

4.2 Network Architecture

본 연구에서 제안하는 DSTAGNN 모델의 아키텍처는 다음과 같습니다.

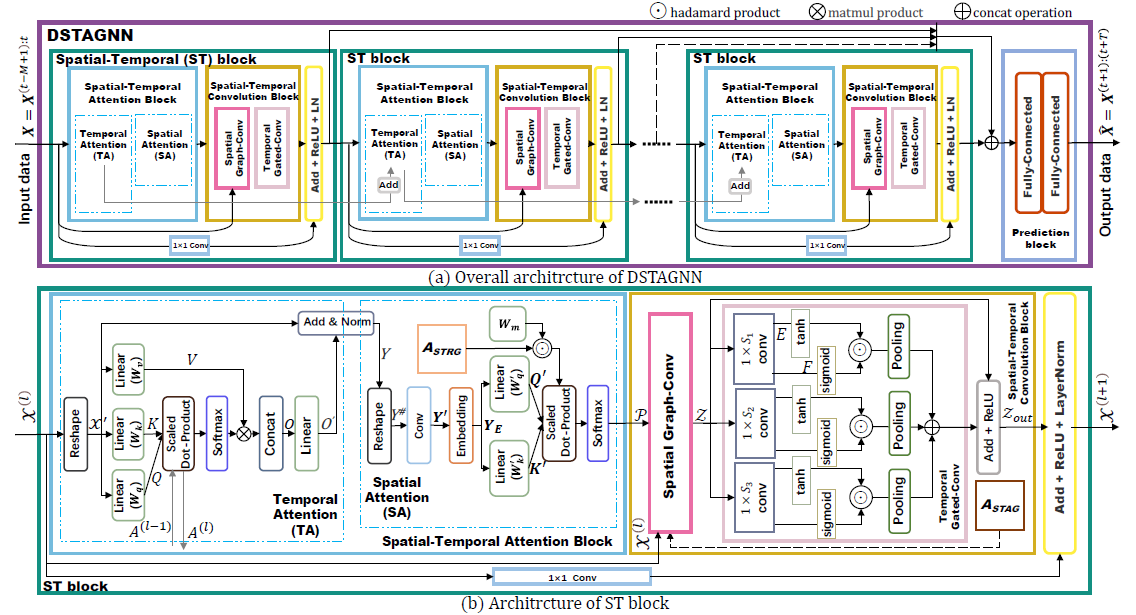
[Figure 3. Detailed Framework of DSTAGNN]

위 (a)는 DSTAGNN의 전체적인 구조를 설명하는 이미지입니다.
DSTAGNN 은 여러 개의 ST Block(Spatial-Temporal(ST) Block) 와 Prediction Block 으로 구성된 아키텍처입니다.

그리고 하단의 (b)는 ST Block(Spatial-Temporal Block)의 세부적인 아키텍처를 설명하는 이미지입니다.
ST Block 은 크게 STA Block(Spatial-Temporal Attention Block) 과 STC Block(Spatial-Temporal Convolution Block) 으로 구성돼있습니다.

각 블럭 모두 Spatial한 요소와 Temporal한 요소를 파악하려고 했다는 점이 포인트입니다.

4.2.1 Spatial-Temporal Aware Graph Contruction

: 도로 네트워크에서 노드 간 연결성(connectivity)를 잘 나타내는 것은 중요합니다. 이러한 연결성은 Spatial Dependency(공간적 의존성)이라고 했었습니다.

기존 GCN에서는 이를 나타내기 위해 인접 행렬(Adjacency Matrix)을 사용했었지만, 다음과 같은 한계가 있다고 했었습니다.
(1) 인접 노드 간의 Traffic Flow 전파의 동적인 효과를 잘 표현하지 못함. (2) 노드 간 거리가 떨어져 있어도 기능적으로 유사한 노드의 유사한 패턴을 잘 포착하지 못함.

이를 위해 각 노드의 확률 분포(Probability Distribution)를 이용해서 Dynamic Spatial Dependency를 파악 하고자 합니다.
바로 앞에서 다루었던 Wasserstein Distance를 이용하려는 것이죠. Wasserstein Distance는 다른 metric에 비해 확률분포의 형태가 다르거나, support가 다르더라도 유용하게 거리를 계산할 수 있는 metric입니다.

먼저 각 노드의 Probability Distribution을 생성 합니다. 이때 우리가 어떤 Graph signal을 사용하냐에 따라 다르겠지만, 본 연구에서는 Traffic volume(교통량)을 예측하고자 하므로, 노드별 Traffic volume에 대한 확률분포를 생성합니다.

이후 Wasserstein Distance를 이용해 각 노드별 확률분포 간의 거리를 계산 합니다. 여기서 ‘거리’는 두 분포의 유사성을 의미한다고 했었습니다.
직관적으로 거리가 가까울수록 두 노드의 Traffic volume의 패턴이 유사하여 서로 의존성이 높은 노드라고 이해한다고 했습니다.

이렇게 계산한 거리를 Spatial-Temporal Aware Distance(STAD) 라고 합시다.
그리고 이 거리를 바탕으로 한 그래프 구조를 Spatial-Temporal Aware Graph(STAG) 라고 하겠습니다.

본격적으로 개념을 정의해보겠습니다.
N개의 노드 로부터 D days동안 수집한 Traffic volume 데이터 $X^{f} \in \mathbb{R}^{D\times d_t \times N}$을 가정하겠습니다. 여기서 $d_t$는 일별 recording times의 수 입니다. 만약 5분 간격으로 수집했다면, 1일 동안의 $d_t$는 288(=12x24)입니다.
이를 벡터 시퀀스로 표현하면 $\mathbf{X}^f_n = (w_{n1}, w_{n2}, \ldots, w_{nD}), w_{nd} \in \mathbb{R}^{d_t}, d \in [1, D]$ 입니다.
여기서 $w_{nd}$는 d번째 일에 n번째 노드에서 측정된 Traffic volume이 되겠죠.

이를 바탕으로 각 노드에서의 daily traffic volume information을 구해보겠습니다. $m_{nd} = \frac{\left\|w_{nd} \right\|_{2}}{Z_n} \,, \; \; \; Z_{n} = \sum^{D}_{d=1} \left\|w_{nd} \right\|_{2}$

위 과정을 통해 n번째 노드의 벡터 시퀀스는 확률 분포 $P_{n}(X_{d} = m_{nd})$ 으로 변환될 수 있는 것이죠.

우리는 이 $m_{nd}$를 일종의 각 일별(d) 확률 질량이라고 해석할 수 있습니다. 그러므로 0과 1 사이의 값을 갖고, 이 질량의 총합은 1을 만족하는 것이죠. 즉 각 노드의 교통량 데이터를 일종의 확률 분포로 변환하여 각 노드의 교통상태를 표현할 수 있고, 이는 하루 중 해당 노드를 통과하는 차량의 상대적인 통행량의 비율이라고 할 수 있습니다.

$m_{nd}$는 시간의 흐름, 즉 d일에 따라 바뀝니다. 그러므로 한 타임 스텝에서 다른 타임 스텝으로의 확률 분포 변화를 수치적으로 측정해볼 수 있겠죠. 일종의 변환 비용이라고 할 수 있겠습니다. 이를 위해서 앞에서 다룬 Wasserstein Distance를 사용하겠습니다.

$d_{STAD}(n_1, n_2) \overset{\text{def}}{=} STAD(\mathbf{X_{n1}}, \mathbf{X_{n2}}) = \inf\limits_{\gamma \in \Pi[P_{n1}, P_{n2}]} \int_{x} \int_{y} \gamma(x,y) \left(1 - \frac{w^T_{n_{1}x} \cdot w_{n_{2}y}}{\sqrt{w^T_{n_{1}x}w_{n_{1}x}} \times \sqrt{w^T_{n_{2}y}w_{n_{2}y}}}\right)dxdy$

그리고 다음과 같은 제약조건을 joint pdf에 추가합니다.

Wasserstein Distance 는 모든 결합확률분포 중에서 distance $d(x,y)$ 의 기댓값을 가장 작게 추정한 값, 최소 거리를 찾는 연산 이라고 했습니다. 이때 STAD에서는 이 $d(x,y)$ 로 cosine distance 를 사용했다는 것이 특징입니다.

즉 두 벡터가 유사할수록 거리는 작게 측정이 되겠죠. 이는 일종의 비용 함수(cost function) 으로 생각해볼 수 있습니다. 거리가 작다는 것은 비용도 작다는 것이겠죠. Wasserstein Distance는 한 지점에서 다른 지점으로 질량(mass)을 옮기는 데 필요한 최소 비용을 계산하는 metric이니깐요.

그래서 이렇게 구한 $d_{STAD}$로부터 다음 행렬을 정의하겠습니다. $\mathbf{A}_{STAD} \in \mathbb{R}^{N\times N}, \; \; \mathbf{A}_{STAD}[i,j] = 1 - d_{STAD}(i,j) \in [0, 1]$

이는 각 노드 간의 상관 정도를 나타내는 행렬이라고 이해할 수 있습니다. 즉 두 노드가 유사할수록 1에 가까운 값을 갖겠죠. 그러므로 이 행렬에서 i번째 행은 i번째 노드와 연결된 N개의 노드들 간의 연결성을 의미하겠죠. 여기서 특정 기준(Sparsity Level) $P_{sp}$에 따라 중요한 값만 유지하고 중요하지 않은 노드들은 0으로 설정하겠습니다. 즉 i번째 행(i번째 노드)에서 각 column을 의미하는 $N$개의 노드 중 $N_{r} = N \times P_{sp}$ 개의 높은 값들만 value를 유지하고, 나머지 값들은 0으로 변환하겠습니다.

이를 통해 새로운 행렬인 Spatial-Temporal Relevance Graph $A_{STRG}$를 얻을 수 있습니다. 이 행렬을 Spatial-Temporal Attention Module 에서 prior knowledge 으로 활용할 예정입니다.

그리고 $A_{STRG}$를 binarizing함으로써 $A_{STAG}$ 행렬을 얻을 수 있습니다. 이는 행렬 원소의 값이 0이 아니면 1을 부여하고, 그렇지 않으면 0인 행렬입니다. 이 행렬은 Graph Convolution 단계에서 adjacency matrix를 대신해서 사용할 수 있겠죠.

결국 $A_{STAD}$에서 $A_{STRG}$로 넘어가는 과정은 Spatial-Temporal Data에서 중요한 $N_{r}$개의 이웃 관계만을 간추림으로써 Attention과 Graph Convolution에서 중요한 이웃 노드들만의 특성을 효과적으로 집약할 수 있게 하는 매커니즘이라고 할 수 있겠습니다.

4.2.2 Spatial-Temporal Attention Block

: STAD는 기존의 Adjacency matrix를 사용하는 것보다 노드 간의 상호 의존성을 좀 더 정확하게 표현해줄 수 있었습니다. 이 STAD를 이용하여 Dynamic한 특성을 좀 더 반영하기 위해 Spatial-Temporal Attention 을 정의하겠습니다.
이는 Temporal Attention 에 Spatial Attention 을 연속적으로 결합한 형태라고 이해하시면 되겠습니다.

Temporal Attention

Temporal한 특성을 파악하기 위해서는 time series data의 장기간의 상관관계(Long-range Correlation)을 효과적으로 파악하는 아키텍처를 설계해야 합니다. 이를 위해 Multi-Head Self Attention 을 이용하겠습니다.

$H$ 개의 Head가 존재하는 Multi-Head Attention에 대해, 다음과 같은 변수들을 정의하겠습니다.
$\mathcal{X}^{'(l)}W^{(l)}_{q} \overset{\text{def}}{=} Q^{(l)}, \; \; \mathcal{X}^{'(l)}W^{(l)}_{k} \overset{\text{def}}{=} K^{(l)}, \; \; \mathcal{X}^{(l)}W^{(l)}_{V} \overset{\text{def}}{=} V^{(l)}$

여기서 $\mathcal{X}^{‘(l)} \in \mathbb{R}^{c^{(l-1)}\times M \times N}$ 은 $l$번째 ST Block의 input인 $\mathcal{X}^{(l)} \in \mathbb{R}^{N \times c^{(l-1)}\times M}$ 의 Transpose입니다. 그리고 $W^{(l)}_{q, k, v}$ 는 어텐션 네트워크에서 Query, Key, Value에 대한 가중치 행렬이라고 이해하시면 되겠습니다.

그리고 다음과 같이 Attention Score 를 정의할 수 있습니다.

$ Att(Q^{(l)}, K^{(l)}, V^{(l)}) = Softmax(A^{(l)})\,V^{(l)}, \;\; A^{(l)} = \frac{Q^{(l)}K^{(l)^{T}}}{\sqrt{d_h}} + A^{(l-1)} $

여기서 Residual Learning 의 아이디어를 활용하기 위해 $A^{(l)}$을 정의합니다. $A^{(l)}$은 Query와 Key의 내적에 기반한 Score인데요. $\sqrt{d_h} = \frac{d}{H}$ 은 일종의 스케일링을 위한 텀입니다.

잔차 학습(Residual Learning) 은 심층 신경망의 학습을 용이하게 하는 기술로, 특히 깊은 네트워크에서 Vanishing Gradient 문제를 완화하는 데 도움을 줍니다. 즉 $A^{(l)}$ 에 이전 레이어의 어텐션 맵 $A^{(l-1)}$ 을 더함으로써 레이어 간 정보의 흐름을 향상시키고, 깊은 레이어에서 그래디언트가 소실되는 문제를 방지합니다.
또한 잔차 연결을 통해 얕은 특성(Low level)과 깊은 특성(High level)을 모두 효과적으로 활용할 수 있는 아이디어입니다.

위에서 H개의 head를 갖고 있는 Multi-Head Attention 구조를 설명했습니다. 그러므로 각 어텐션 헤드로부터 얻은 H개의 output을 다음과 같이 정의할 수 있습니다.

$ O^{(h)} = Att(QW^{(h)}_q, KW^{(h)}_k, VW^{(h)}_v ) \; , \; h = 1, 2, \cdots , H$

그리고 이 H개의 Output을 concatenation해서 $O$ 를 다음과 같이 정의할 수 있습니다. 이 과정은 서로 다른 어텐션 헤드로부터 얻은 정보를 축약하는 과정이라고 보시면 되겠습니다.

$ O = [O^{(1)}, O^{(2)}, \cdots, O^{(H)}] $

그러면 이를 Linear Layer(Fully-connected Layer)의 input으로 활용함으로써 output인 $O^{‘} \in \mathbb{R}^{c^{(l-1)} \times M \times N}$ 을 얻게 되고, 이 $O^{‘}$와 $\mathcal{X}^{‘(l)}$의 잔차 연결을 통해 Normalization층을 통과시킴으로써 output $Y \in \mathbb{R}^{c^{(l-1)} \times M \times N}$ 를 얻게 됩니다.

$ Y = LayerNorm(Linear(O^{‘} + \mathcal{X}^{‘}))$

이 $Y$는 다음 단계인 Spatial Attention(SA) Module의 Input 이 됩니다.
Spatial Attention

앞선 TA Module을 통해 모델의 input인 Time series data의 전역적인 dynamic temporal dependencies를 갖는 feature representation을 추출할 수 있었습니다. 이 feature representation인 $Y$ 을 바탕으로 SA Module에서는 공간 의존성(Spatial Dependency)을 파악하기 위한 self-attention을 고안 하였습니다.

먼저 Input인 $Y$를 $Y^{\text{#}} \in \mathbb{R}^{c^{(l-1)} \times N \times M}$ 로 Transpose하겠습니다. 그리고 time dimension $M$을 고차원 공간인 $d_E$로 매핑하고, 1차원 컨볼루션을 통해 Feature dimension $c^{(l-1)}$을 집계하여 새로운 행렬 $\mathbf{Y}^{‘} \in \mathbb{R}^{N \times d_{E}}$을 생성합니다. 즉 $\mathbf{Y}^{‘}$ 는 각 Node의 Embedded Vector Representation 이라고 할 수 있습니다.

여기에 노드의 위치 정보를 추가하기 위해 $\mathbf{Y}^{‘}$에 임베딩 레이어를 적용하여 $\mathbf{Y}_E$ 를 얻습니다. 이는 Positional Encodding을 추가 한 것으로 이해할 수 있습니다.

$\mathbf{Y_E}$ 와 3.2.1절에서 제안한 $A_{STRG}$ 를 이용해 H개의 헤드를 가진 새로운 Spatial Attention 을 다음과 같이 제안하였습니다.

$W^{‘(h)}_k, W^{‘(h)}_q \in \mathbb{R}^{d_E \times d_h}, W^{(h)}_m \in \mathbb{R}^{N \times N}$ 은 모두 가중치 행렬입니다. 핵심은 위 어텐션 네트워크에서 $\mathbf{Y} W^{‘(h)}_k$ 는 Key로, $\mathbf{Y} W^{‘(h)}_q$ 는 Query로서 역할을 한다면 Value의 역할을 $A_{STRG}$ 가 한다는 것 입니다.

Spatial-Temporal Relevance Graph, $A_{STRG}$ 는 도로 네트워크에서 각 노드마다 가장 관련성 높은 노드들의 중요도를 제공하는 행렬이었습니다. 즉 Spatial Dependency를 의미하는 것이었죠. 기존 트랜스포머에서 쓰였던 Value를 $A_{STRG}$ 로 대체함으로써 Spatial Attention의 성능을 향상시키는 것이 핵심입니다.

H개의 어텐션 헤드를 결합하면 다음과 같은 $\mathcal{P} \in \mathbb{R}^{H \times N \times N}, \; P^{(h)} \in \mathbb{R}^{N \times N}$ 이 도출됩니다.

$ \mathcal{P} = [P^{(1)}, P^{(2)}, \cdots , P^{(H)}] $

이 output $\mathcal{P}$ 는 TA module과 SA module을 통과해서 나온 Dynamic Spatial-Temporal Attention Tensor 입니다. 이를 활용해 Graph Convolution Layer에서 Input으로 활용하겠습니다.

4.2.3 Spatial-Temporal Convolution Block

: 기존 GCN에서는 도로 네트워크 내에서 노드 간의 connectivity를 표현하기 위해 adjacency matrix를 활용했고, 이를 이용해 이웃 노드들의 정보를 집약해서 node feature를 추출했다고 했었습니다. 하지만 이는 단순히 이웃하였다고 중요한 노드가 아니라는 점, 그리고 이웃하지 않더라도 기능적으로 유사하다면 충분히 dependent한 노드라는 점 등의 이유로 adjacency matrix는 효과적이지 않다고 했었습니다.

Spatial Graph Convolution

이러한 한계를 근거로 Spatial-Temporal Aware Graph 를 새롭게 정의했었습니다. STAG는 1 아니면 0으로 이루어진 행렬이었죠. 이를 활용해 Spatial Graph Convolution을 정의하겠습니다.

먼저 Chebyshev Polynomial Expansion 을 활용하기 위해 Scaled Laplacian Matrix 를 정의하겠습니다.
$ \tilde{L} = \frac{2}{\lambda_{max}}(D - A^{*}) - I_{N} $

여기서 $A^{*} = A_{STAG}$이고, $I_{N}$은 Identity Matrix입니다. 그리고 $D \in \mathbb{R}^{N \times N}$ 은 degree matrix, 즉 각 노드의 degree(차수)를 나타내는 대각행렬으로, 대각성분 $D_{ii} = \Sigma_{j}A^{*}_{ij}$ 와 같습니다.
$\lambda_{max}$는 Laplacian Matrix의 maximum eigenvalue입니다.

Laplacian Matrix를 스케일링한 이유는 라플라시안 행렬의 고유값 범위를 조절하기 위함입니다. K차 체비셰프 다항식은 재귀적으로 연산을 하는데, 이때 라플라시안 행렬의 거듭제곱시 각 원소의 값이 커지는 것을 조절하고, 안정적이고 효율적인 연산을 가능하게 합니다.

이제 Scaled Laplacian Matrix에 K차 체비셰프 다항식 $T_{k}$ 을 이용해 Spatial Graph Convolution을 정의하겠습니다.
$g_{\theta} \, * \, G_{x} = g_{\theta}(L)x = \sum^{K-1}_{k=0}\theta_{k}(T_{k}(\tilde{L}) \; \odot \; P^{(k)} )\,x$
- $g_{\theta}$ : Approximate Convolution Kernel
- $*G$ : Graph Convolution Operation
- $\mathbf{\theta} \in \mathbb{R}^{K}$ : Polynomial Coefficient
- $P^{(k)} \in \mathbb{R}^{N \times N}$ : ST Attention of k-th head
- $x$ : Graph signal(traffic volume)
위 Graph Convolution 연산에 앞에서 정의한 Dynamic Spatial-Temporal Attention Tensor를 입력으로 사용하여 각 체비셰프 항에 대한 Attention 가중치를 element-wise로 연산하는 과정은 그 항이 갖는 정보의 중요도를 조절하는 과정입니다.

즉, 어떤 노드에 대해 바로 인접한 이웃(k=1)의 정보가 특히 중요하다고 판단될 경우, 해당하는 체비셰프 다항식 항에 높은 attention 가중치를 할당함으로써 그 영향력을 강조할 수 있습니다. 이를 통해 각 노드는 0부터 (K-1)차항의 이웃 노드들의 정보를 시간과 공간에 걸쳐 효과적으로 집약할 수 있습니다.

Temporal Gated Convolution

앞선 Spatial Graph Convolution 에서 노드 간의 공간적인 의존성을 파악하고자 했다면, Temporal Gated Convolution 에서는 장기 및 단기 기간의 Temporal Dynamic Information을 포착하기 위해 Multi-Scale Gated Tanh Unit(M-GTU) 을 제안했습니다.

이 방법은 기존의 GTU(Gated Tanh Unit)을 확장하여 만들었으며, 서로 다른 크기의 수용 영역(Receptive Field)을 가진 세 개의 GTU 모듈을 사용 합니다.

기존 GTU는 다음과 같이 정의됩니다. $\Gamma \, * \, Z^{l} = \phi(E) \, \odot \, \sigma(F)$
- $\Gamma \in \mathbb{R}^{1 \times S \times c^{(l)} \times 2c^{(l)}}$ : Convolution kernel with kernel size $1 \times S$
- $Z^{(l)}$ : l-th layer’s input
- $\phi, \, \sigma$ : Activation Function(Tanh and Sigmoid)
- $E, F$ : first half and second half of $Z^{(l)}$
즉 GTU는 tanh 함수와 sigmoid 함수를 이용하여 입력의 gating 매커니즘을 구현하는 것입니다. 이는 네트워크가 입력 데이터에서 중요한 정보를 선택적으로 통과시키도록 합니다.

이 GTU를 기반으로 본 연구에서 제안한 M-GTU(Multi-Scale Gated Tanh Unit) 을 정의하겠습니다.
$Z^{(l)}_{out} = M-GTU(Z^{(l)}) = ReLU(Concat(Pooling(\Gamma_1 \, *_{\tau} \, Z^{(l)}), Pooling(\Gamma_2 \, *_{\tau} \, Z^{(2)}), Pooling(\Gamma_3 \, *_{\tau} \, Z^{(3)})) + Z^{(l)})$
- $\Gamma_{1,2,3}$ : Convolution Kernels with size $1 \times S_{1,2,3}$
M-GTU는 다양한 크기의 수용 영역을 가진 세개의 GTU 모듈의 출력을 결합하여 장기 및 단기의 시간적 패턴을 모두 포착할 수 있게 합니다.
추가적으로 입력과 M-GTU 출력에 $Z^{(l)}$을 더해주는 Skip Connection 을 적용함으로써, 네트워크가 깊어질 때 발생할 수 있는 Vanishing Gradient 문제를 완화하도록 설계하였습니다.

이러한 구조를 통해 다양한 범위의 Temporal Dependency를 효과적으로 모델링할 수 있습니다.

5. Experiments

그러면 본 연구에서 제안한 Model인 DSTAGNN의 성능은 얼마나 좋을까요? 이번 챕터에서는 실제 데이터를 바탕으로 DSTAGNN의 퍼포먼스를 확인해보겠습니다.

5.1 Experiment settings

: 본 연구에서는 Califonia의 실제 도로 네트워크에서 측정된 4개의 데이터셋 을 활용했습니다. 데이터는 5분 간격으로 수집되었으며, 평균이 0이 되도록 정규화를 진행하였습니다.

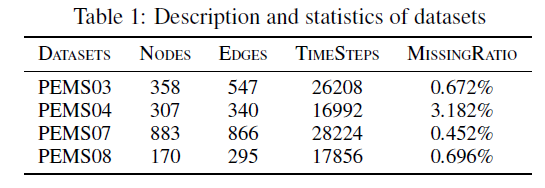
[Table 1. Description and Statistics of Datasets]

평가 지표로는 RMSE, MAE, MAPE 3개의 지표 를 활용하였습니다.
그리고 다음과 같이 Hyperparameter를 설정하였습니다.

$K = 3$ : The number of terms of the Chebyshev Polynomial
${S_{1}, S_{2}, S_{3}} = {3,5,7}$ : The size of M-GTU Convolution kernel
$W = 2$ : Window size of pooling layer
$H = 3$ : The number of attention heads in the TA Module
$d_{h} = 32$ : Scailing Term
32 Convolution Kernels in All Graph Convolution layers
4 ST Blocks
Loss function : Huble Loss
Optimizer : Adam
Epochs : 100
Learning rate : 0.0001
Batch size : 32
$P_{sp} = 0.01$ : Hyper-Parameter of Sparsity

DSTAGNN 모델과 성능을 비교하기 위해 다음과 같은 Baseline methods 를 설정하였습니다.

(1) FC-LSTM : Special RNN
(2) TCN : Applied learning local and global temporal relations
(3) DCRNN : Integrated graph convolution into a gated recurrent unit
(4) STGCN: Integrated graph convolution into a 1D convolution unit
(5) ASTGCN(r) : Spatial-Temporal attention machanism in the model
(6) STSGCN : Local Spatial-Temporal subgraph modules
(7) STFGNN : Spatial-Temporal fusion graph to complement the spatial correlation
(8) STGODE : Applied continuous graph neural network to traffic prediction in multivariate time series forecasting
(9) Z-GCNETs : Applied concept of zigzag persistence into time-aware graph convolutional network
(10) AGCRN : Exploited learnable embedding of nodes in graph convolution

5.2 Experiment results and analysis

: 실험 결과는 다음과 같습니다.

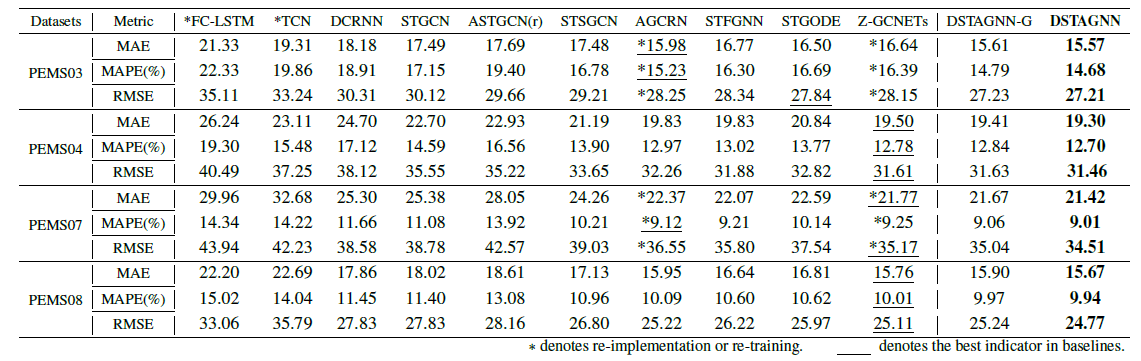
[Table 2. Performance comparison of our DSTAGNN and baseline models on PEMS datasets]

위 테이블을 통해 우리는 DSTAGNN 모델이 모든 데이터셋과 metric에서 베이스라인 모델에 비해 좋은 Performance를 보여주고 있음을 알 수 있습니다.

DSTAGNN-G는 $A_{STAG}$ 대신 adjacency matrix를 사용한 DSTAGNN 모델입니다. 하단의 결과를 통해 알 수 있듯이, Spatial-Temporal Aware Graph는 예측 성능을 향상시키는 데 주요한 역할을 하고 있음을 알 수 있습니다.

대체로 베이스라인에서는 AGCRN과 Z-GCNETs 모델이 좋은 성능을 보여주었는데, 이는 두 모델이 다른 모델에 비해 Spatial-Temporal 특성을 잘 추출했기 때문입니다. 그럼에도 DSTAGNN은 데이터의 동적 변화와 Spatial-Temporal 특성을 더욱 잘 추출하기 위해 Spatial-Temporal Aware Graph를 활용하였으며, ST Block이라는 아키텍처를 통해 이러한 성능을 크게 향상시킴으로써 좋은 퍼포먼스를 보였음을 직관적으로 확인할 수 있습니다.

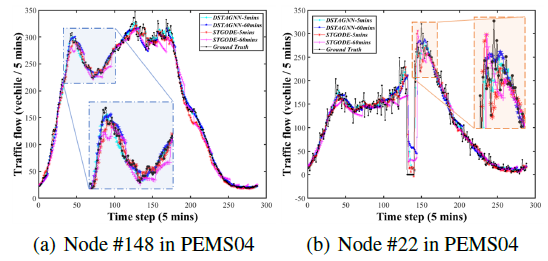
[Figure 4. Comparison of prediction curves between STGODE and DSTAGNN in PEMS04]

위 Figure 4를 통해 STGODE와 DSTAGNN의 예측 성능을 직관적으로 확인할 수 있습니다. 대체로 Ground Truth의 Trend는 두 모델 모두 잘 포착하고 있으나, 일부 변칙적인 패턴을 보이는 구간에서는 STGODE가 잘 파악하지 못하는 경향이 있습니다. 그러나 DSTAGNN은 그러한 구간에서도 잘 예측하는 것을 알 수 있으며, 특히 (b)에서 불규칙하게 바뀌는 구간에서도 최대한 패턴을 잘 추척하고 있음을 알 수 있습니다.

본 연구에서 제안하는 각 개별 구성요소의 효과를 검증하기 위해, 각 요소를 하나씩 제거함으로써 성능을 비교하는 실험 또한 진행하였습니다.

(1) RemSTA : ST Attention Module을 제거
(2) RemM-A : Multi-Heads Attention Module을 제거
(3) RemM-GTU : M-GTU를 제거 (traditional convolution으로 대체)
(4) RemRC-OUT : 각 ST Block의 Residual Connection을 제거

결과는 다음과 같습니다.

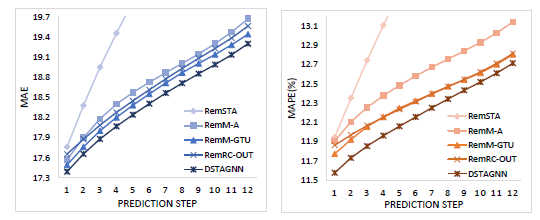
[Figure 5. Ablation experiment of module effectiveness]

즉 Prediction step이 증가함에도 각 요소를 제거한 모델의 성능보다 DSTAGNN의 성능이 더욱 좋음을 알 수 있습니다.

흥미로운 점은 RemSTA의 성능이 제일 떨어진다는 것 인데요. 이를 통해 DSTAGNN 모델에서 Spatial-Temporal Attention Module이 차지하는 역할이 크다는 것 을 알 수 있겠습니다.

5.3 Visualization of Spatial-Temporal Dependency

: DSTAGNN으로부터 얻은 Spatial-Temporal Dependency를 확인하기 위해 다음과 같이 시각화된 도로 네트워크 이미지를 확인해보겠습니다.

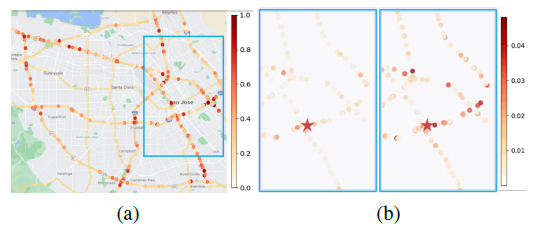
[Figure 6. Spatial-Temporal Dependency obtained by DSTAGNN on the PEMS-BAY Dataset]

(a)는 도로 네트워크의 교차로와 같은 복잡한 교통 상황을 식별할 수 있음 을 직관적으로 보여줍니다. 즉, Target Node에서 발생하는 교통량 증가가 인접 노드뿐만 아니라 먼 거리에 있는 노드에도 영향을 줄 수 있음을 의미합니다. 이는 1번째 Attention Head로부터 획득한 전역적인 정보입니다.

(b)는 모델이 Target Node(Red Star로 도식)에 대해 Dynamic Spatial Dependency를 어떻게 획득하는지 보여줍니다. 시간의 흐름에 따라 Target Node와 주변 노드와의 의존성이 달라짐을 확인할 수 있으며, 이는 2번째, 3번째 Attention Head로부터 획득한 정보입니다. 이 의존성 정보는 특정 시간대에 목표 노드에 가장 큰 영향을 미치는 주변 노드들을 식별하는 데 도움을 줍니다.

6. Conclusion

본 논문에서 제안한 DSTAGNN은 기존 GCN에서 활용하던 사전 정의된 정적인 인접행렬을 사용하지 않고, 과거의 데이터로부터 획득한 Spatial-Temporal Aware Distance(STAD)를 새롭게 정의 후 사용함으로써 도로 네트워크 내 노드 간의 Dynamic Association 속성의 특징을 잘 추출하고 표현 할 수 있었습니다.

또한 STAD로부터 생성된 Spatial-Temporal Aware Graph 위에서 작동하는 그래프 컨볼루션은 도로 네트워크의 사전 정보에 대한 의존성을 줄일 수 있었습니다. 즉, 단순히 인접한 이웃 노드의 정보를 집계하는 것이 아닌, 인접하지 않더라도 관련성이 높은 노드들까지 이웃의 범위를 확장함으로써 Spatial Dependency를 적극적으로 고려하였습니다.

이뿐만 아니라 Spatial-Temporal Attention Module과 M-GTU 아키텍처를 통해 Traffic Forecasting 성능을 비약적으로 높였습니다. 이를 통해 지금까지의 Traffic forecasting을 위한 연구들에서 고려하지 못한 Dynamic Spatial-Temporal Dependency를 고려하는 것이 중요함을 강조함으로써, 앞으로의 교통 분야에서의 Graph Neural Networks의 발전 방향에 이정표를 제시했다고 생각합니다.

Author Information

Minwoo Jeong (GSDS)
- Affiliation : TRUE Lab(Transportation Research and Urban Engineeting LAB)
- Research Topic : Graph Neural Network, Urban Air Mobility, Spatial-Temporal Data Mining
- Contact : minwoo5003@kaist.ac.kr

Reference

[ICML 2022] DSTAGNN: Dynamic Spatial-Temporal Aware Graph Neural Network for Traffic Flow Forecasting
Berndt, D. J. and Clifford, J. Using dynamic time warping to find patterns in time series. In KDD workshop, volume 10, pp. 359–370. Seattle, WA, USA:, 1994.
Li, M. and Zhu, Z. Spatial-temporal fusion graph neural networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pp. 4189–4196, 2021.
Li, Y. and Shahabi, C. A brief overview of machine learning methods for short-term traffic forecasting and future directions. Sigspatial Special, 10(1):3–9, 2018.
Li, Y., Yu, R., Shahabi, C., and Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv preprint arXiv:1707.01926, 2017.
Yu, B., Yin, H., and Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv preprint arXiv:1709.04875, 2017.
Zhang, J., Zheng, Y., Qi, D., Li, R., and Yi, X. Dnn-based prediction model for spatio-temporal data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, pp. 1–4, 2016.
Zhao, L., Song, Y., Zhang, C., Liu, Y., Wang, P., Lin, T., Deng, M., and Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE Transactions on Intelligent Transportation Systems, 21(9):3848–3858, 2019.