DAGAD: Data Augmentation for Graph Anomaly Detection

1. Problem Definition

Classification 등의 downstream task에 악영향을 미치는 anomalous sample을 탐지한다.

한 그룹 내에서 다른 대다수의 경우와 동떨어진 behavior를 보이는 무언가를 anomaly라고 부릅니다. Real-world에서의 예시로는 가짜 뉴스, SNS 상의 허위/스팸 계정, 불법 거래 등이 있습니다. 이러한 real-world scenario는 각각의 data sample(ex. SNS 사용자)을 node로, sample 간의 관계(ex. 팔로우 유무)를 edge로 정의해 graph data로 표현할 수 있습니다. Graph data 내에서 real-world anomaly는 anomalous node(ex. 스팸 유저와 같은 single object)나 anomalous edge(ex. 불법 거래와 같은 interaction) 등으로 묘사됩니다. 이 논문은 graph data 속에서 anomalous node를 찾는 Graph Anomaly Detection task에 대해 설명합니다.

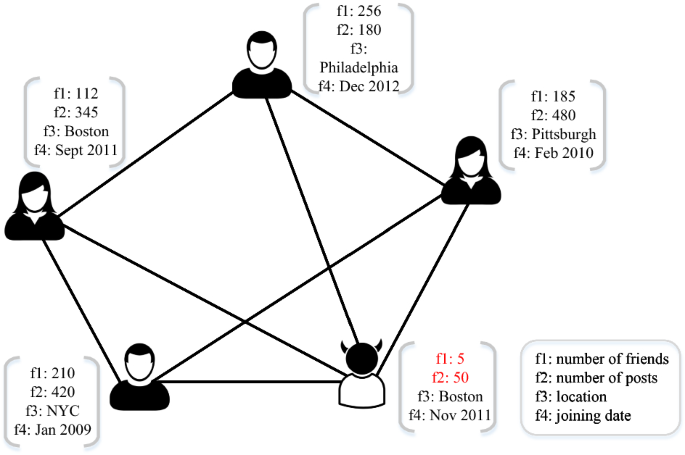
image



2. Motivation

Graph Anomaly Detection에서 흔히 발생하는 문제를 해결한다.

Graph anomaly detection(이하 GAD)을 다룬 이전 연구들은 이미 존재하는 graph topological information(node들이 edge로 어떻게 연결되어 있는지에 관한 정보)과 attribute information(node 각각의 정보)을 통해 anomaly를 찾습니다. 하지만 이러한 method는 data에 내재되어 있는 두 가지 문제에 직면합니다.

첫 번째 문제는 anomalous sample scarcity입니다. Real-world anomaly에 대한 sample을 얻는 것은 쉬운 일이 아닙니다. 예시로 Alipay라는 결제 사이트에서 피해를 본 사례의 약 90%는 보고되지 않았다고 합니다. 이러한 상황에서 GAD 모델은 적은 양의 anomaly밖에 관측할 수 없습니다.

두 번째 문제는 class imbalance입니다. Anomalous sample의 양은 적은 반면 상대적으로 normal(즉 anomaly가 아닌) sample의 양은 훨씬 많은 경우가 대부분입니다. 이 때문에 GAD는 anomaly의 관점에서 굉장히 skewed 된 distribution에서 수행되게 됩니다.

이 두 가지 문제로 인해 이전 연구들은 subpar한 performance를 보입니다. 이를 해결하기 위해 이 논문은 Data Augmentation-based Graph Anomaly Detection framework(DAGAD)을 제안합니다. DAGAD는 data sample을 추가로 생성해 training set에 추가하고 class-wise loss를 통해 학습하는데, 이 두 방법을 통해 앞서 설명한 두 가지 문제가 끼치는 악영향을 완화할 수 있습니다.



3. Method

Preliminaries

논문에서 제안한 방법론을 이해하기 위해서 problem formulation을 포함해 몇 가지 definition에 대해 소개하겠습니다.

$\mathcal{G} = (\mathcal{V}, \mathcal{E}, \mathcal{A}, \mathcal{X})$는 $n$개의 node를 가진 attributed graph, 즉 각 node가 attribute 정보를 가진 graph를 의미합니다. 여기서 $\mathcal{V}, \mathcal{E}$는 각각 node set ${v_ i}_ {i = 1}^ {n}$, edge set ${e_ {ij}}$를 나타내고, $e_ {ij} = (v_ i, v_ j)$는 두 node $v_ i$와 $v_ j$ 사이를 잇는 edge가 있음을 뜻합니다. $\mathcal{A} \in {0,1}^ {n \times n}$은 $\mathcal{G}$의 topological structure를 나타내는 adjacency matrix인데, $\mathcal{A}$의 각 element $a_ {ij}$에 대해 $e_ {ij} \in \mathcal{E}$라면 $a_ {ij} = 1$, 그렇지 않다면 $a_ {ij} = 0$입니다. Attribute matrix $\mathcal{X} \in \mathbb{R}^ {n \times k}$에는 각 node $n_ i$의 $k$-dimensional attribute $x_ i$가 들어갑니다.

Attributed graph $\mathcal{G}$가 주어졌을 때, GAD task는 binary classification task로 치환될 수 있습니다. 이는 각 node $v_ i$에 대해 $v_ i$가 anomaly라면 1을, 그렇지 않다면(즉 normal node라면) 0을 label로 부여하는 것을 의미합니다(i.e. $\mathcal{V} \to Y \in {0,1}^ n$). 이 논문에서 DAGAD는 label이 무엇인지 아는 소수의 node를 통해 나머지 node의 label을 예측하는 task를 수행합니다.



Proposed Framework

이제 본격적으로 DAGAD에 대해서 살펴보겠습니다. 먼저 전체 framework를 간략히 소개하겠습니다.

image

위 figure에서 볼 수 있듯이, DAGAD는 3개의 module의 collaboration으로 이루어져 있습니다. 먼저 Information Fusion Module은 2개의 GNN encoder를 통해 graph topology와 node attribute, 2개의 관점에 대해서 각각 node representation을 구합니다. 그 다음 Data Augmentation Module이 앞서 학습한 representation을 기반으로 추가 sample을 생성해 training set에 추가합니다. 이후 Imbalance-tailored Learning Module은 anomaly와 normal node의 차이가 드러나도록 학습하고, 이때 class-wise loss를 통해 class imbalance 문제를 완화할 수 있습니다. 이 3개의 module로 구한 output을 기반으로 각 node의 label(normal 또는 anomalous)을 최종적으로 예측하게 됩니다.

아래에서 각 module에 대해 더 자세히 설명하겠습니다.



A. Information Fusion Module

Node attribute 정보의 방대함과 graph topology 정보의 복잡성으로 인해, 기존 graph data를 그대로 가지고 GAD를 수행하는 것은 쉽지 않습니다. 때문에 DAGAD는 encoder를 통해 구한 low-dimensional representation으로 anomaly와 normal node를 구분합니다. 이때 encoder는 $\phi : {\mathcal{A,X}} \to H \in \mathbb{R}^ {n \times d}$의 형태를 띄는데, 여기서 $H$는 각 node $v_ i$에 대해 $d \ll k$를 만족하는 $h_ i \in \mathcal{R}_ d$로 이루어져 있습니다.

DAGAD는 graph 정보 representation에서 좋은 성능을 보이는 GNN 모델을 encoder로써 차용해 neighborhood 정보를 aggregate하는데, 그 형태는 다음과 같습니다:

image

위 식에서 $h_ i ^ l$은 GNN의 $l$번째 layer에서 node $v_ i$의 representation을 의미하고, set $\mathcal{N}(i)$는 $v_ i$의 neighborhood에 있는 나머지 node들로 이루어져 있습니다. 또한 $f_ {AGG}(\cdot)$는 node representation을 aggregate(sum, mean 등)하는 역할을 하고, 이때 initial representation은 node attribute입니다(i.e. $h_i ^ 0 = x_ i$).



B. Data Augmentation Module

Information fusion module에서 학습한 representation만을 바탕으로 GAD를 수행한다면 suboptimal한 performance에 맞닥뜨리게 됩니다. 이는 소수의 기존 anomalous sample에서 얻은 한정된 정보만을 사용하는 anomaly detector는 anomaly와 normal node를 확실하게 구분하기 어렵기 때문입니다. 여기서 DAGAD의 data augmentation module가 이 anomalous sample scarcity 문제를 완화할 수 있습니다. Graph 구조나 node attribute에 변형을 가하는 다른 augmentation technique과는 달리, DAGAD는 node representation을 바탕으로 새로운 sample을 생성하여 training set에 anomaly에 대한 정보를 풍부하게 하는 것을 목표로 하고 있습니다.



1. Augmentation on Representation

DAGAD의 target은 anomaly와 normal class 간의 boundary를 학습하는 것입니다. 이를 위해 두 classifier $C_ a, C_ b$를 쓰는데, 여기서 $C_ a$는 anomalous class에 overfit하여 anomaly-related feature를 얻는 것을 목적으로 하고, 이를 통해 최종 classifier $C_ b$의 성능을 강화합니다.

우선 training set에 있는 기존 sample을 augment하기 위해 Eq. (1)으로 얻은 representation에 random permutation을 가하는데, 형태는 다음과 같습니다:

image

위 식에서 $\tilde{H}$는 $PERMUTE : h_ i \to \tilde{h_ j} \in \tilde{H}$를 통해 얻은 permuted representation으로 이루어져 있습니다. 다음으로 두 classifier $C_ a, C_ b$가 함께 작동하도록 하기 위해 두 representation을 concatenate하는데(즉 information fusion module에서 2개의 GNN encoder를 학습), 형태는 다음과 같습니다:

image

위 식에서 $h_ i ^ {C_ a}, h_ i ^ {C_ b}$는 각각 $C_ a, C_ b$에 쓰일, 앞선 module에서 학습된 representation을 의미합니다. 같은 논리로 augmented sample은 $C_ a$의 기존 representation과 $C_ b$의 permuted representation을 concatenate하여 구합니다:

image

이때 augmented representation도 $C_ b$의 학습에 쓰이기 때문에, augmented sample의 label도 $\tilde{y} = PERMUTE(y)$에 따라 부여됩니다. 즉 $\tilde{h_ i}^ {C_ b}$의 label이 $\tilde{\mathrm{h}_ i} ^ {C_ b}$의 label이 됩니다.



2. Complementary Learning

이제 augmented representation이 포함된 training set에 대해 두 classifier $C_ a, C_ b$를 complementary하게 학습합니다. 여기서 complementary란 두 classifier가 정보를 주고받으며 상호보완적으로 학습됨을 뜻합니다. 각 classifier에서 fully-connected layer가 2개인 MLP $f^ {MLP}(Z; \theta)$를 통해 각 node의 최종 representation을 구하는데, 여기서 $Z$는 앞서 구한 concatenated representation이고 $\theta$는 학습 가능한 parameter set입니다. Input $\mathrm{h} \in \mathbb{R}^ {2d}$에 대해 MLP의 각 layer는 다음과 같은 형태입니다:

image

위 식에서 $W \in \mathbb{R}^ {D \times 2d}, b \in \mathbb{R}^ D$는 각각 학습 가능한 weights와 bias를 의미하고, 이를 통해 기존 sample과 augmented sample 각각에 대해 최종 representation $\mathrm{h}^ * \in \mathbb{R}^ 2, \tilde{\mathrm{h}}^ * \in \mathbb{R}^ 2$를 구할 수 있습니다. 이후 다음과 같이 softmax function으로 각 node가 anomaly이거나 아닐 확률을 구하고 이를 바탕으로 각 node에 label을 부여합니다:

image image

앞서 언급했듯이 $C_ a, C_ b$는 complementary하게 학습됩니다. 기존 training sample에 대해서 $C_ a$에는 cross entropy (CE) loss를, $C_ b$에는 generalized cross entropy (GCE) loss를 적용합니다. 여기서 $C_ a$는 anomaly class와 가장 연관이 있는 feature를 학습하도록 overfit 시켜, $C_ b$가 anomaly와 normal class를 구분하는 feature를 잘 학습하여 더 좋은 detection 결과가 나오도록 합니다. 요약하자면 $C_ a$는 anomaly를 더 잘 드러내는 feature에 훨씬 집중하도록 학습되어 이 정보를 $C_ b$에 전달하고, $C_ b$는 이 정보를 활용해 anomalous class와 normal class를 더 잘 구분하도록 학습됩니다. 즉, 실제 detection은 $C_ b$에 의해 이루어집니다. 이를 위해 $C_ a$는 anomaly에 더 bias될 수 있도록 weight가 조정된 CE loss로 학습되고(weight에 대한 설명은 다음 module에서 이루어집니다), $C_ b$는 anomaly라는 noise에 좀 더 robust한 GCE loss로 학습됩니다. 이 합쳐진 objective의 형태는 다음과 같습니다:

image

위 식에서 $\psi_ {CE}, \psi_ {GCE}$는 각각 CE loss function과 GCE loss function을 의미하고, $\omega$는 $C_ a, C_ b$ 간에 complementary 정보 교환이 일어나도록 하는데 형태는 다음과 같습니다:

image

$C_ b$는 augmented sample 또한 GCE loss에 넣는데, 이 objective의 형태는 다음과 같습니다:

image

앞서 나온 부분을 모두 통합한 DAGAD의 overall loss function은 다음과 같습니다:

image

이때 $h^ {C_ a}, h^ {C_ b}$가 각각 $C_ a, C_ b$에 의해서 학습이 주로 되도록 하기 위해, $C_ b$에서의 loss는 $h_ i ^ {C_ a}$를 학습하는 encoder로 backpropagate되지 않고, $C_ a$에서의 loss는 $h_ i ^ {C_ b}$를 학습하는 encoder로 backpropagate되지 않습니다.



Imbalance-tailored Learning Module

Imbalanced training data 문제로 인해, GAD에서 normal class에 대한 bias와 anomaly에 대한 under-training이 주로 발생합니다. 학습 과정에 두 class로부터의 contribution의 균형을 맞추기 위해 DAGAD는 Eq. (11)을 기반으로 한 class-wise loss function을 제안합니다. 모든 training sample을 동일하게 취급하지 않고 class별로 다른 weight를 부여하는데, 형태는 다음과 같습니다:

image

위 식에서 $\vert \mathcal{V}_ {train} ^ {anm} \vert, \vert \mathcal{V}_ {train} ^ {norm} \vert$은 각각 training set 내에서 anomaly와 normal sample의 개수를 의미합니다. 이와 비슷하게 새로 class-wise GCE loss를 정의할 수 있는데, 형태는 다음과 같습니다:

image

이를 통해 다음과 같이 Eq. (11) 대신에 새로운 overall loss를 정의할 수 있습니다:

image

이때 $\hat{\mathcal{L}}_ {org} ^ {C_ a}, \hat{\mathcal{L}}_ {org} ^ {C_ b}, \hat{\mathcal{L}}_ {aug} ^ {C_ b}$는 각각 $\mathcal{L}_ {org} ^ {C_ a}, \mathcal{L}_ {org} ^ {C_ b}, \mathcal{L}_ {aug} ^ {C_ b}$에 instance-wise CE loss 와 GCE loss 대신에 Eqs. (13)과 (14)를 적용한 것입니다.



Algorithm

image

위 pseudocode는 앞서 설명한 3개의 module이 DAGAD에서 어떻게 돌아가는지 보여줍니다.



4. Experiment

이 논문은 여러 종류의 실험과 ablation study를 통해 다음 3개의 research question에 답하고자 합니다:

  • Q1: DAGAD는 SOTA baseline method와 비교해 우위를 가지는가?
  • Q2: Data augmentation module이 anomaly detection에 도움을 주는가?
  • Q3: Imbalance-tailored learning module이 anomaly detection에 도움을 주는가?
  • Q4: DAGAD가 sensitive한 hyper-parameter가 있는가?



Experimental Setup

Datasets

다음과 같이 3개의 real-world dataset에 anomaly를 inject해 실험에 사용합니다. 여기서 injection은 DOMINANT라는 논문에서 제안한 scheme에 따라 이루어지는데, 더 자세한 내용은 맨 아래 reference를 통해 확인할 수 있습니다. 이때 training set에는 전체 node의 20%, test set에는 80%를 넣고, 각 set에서 anomaly의 비율은 전체 dataset에서의 비율과 같도록 합니다.

image

Baselines

다음과 같이 10개의 deep graph learning 기반 anomaly detector과 비교합니다.

  • Semi-supervised: GCN-Detector, GAT-Detector, GraphSAGE-Detector, GeniePath-Detector
  • Unsupervised: FdGars, DONE, AdONE, DOMINANT, AnomalyDAE, OCGNN

DAGAD의 경우 GNN encoder로 사용한 모델에 따라 DAGAD-GCN과 DAGAD-GAT로 나누었습니다.

Evaluation Metrics

다음과 같이 5개의 metric으로 detection performance를 측정합니다.

  • Macro-Precision, Macro-Recall, Macro-F1-score, ROC curve, AUC score

이때 semi-supervised detector와는 Macro-Precision, Macro-Recall, F1-score를 비교하고, unsupervised detector와는 ROC curve와 AUC score를 비교합니다.



Detection Performance (Q1)

1. Comparison with Semi-supervised Detectors

image

F1-score의 경우 다른 detector보다 DAGAD의 성능이 높은 것을 확인할 수 있습니다. 이는 DAGAD에서 class imbalance 문제를 완화해주는 class-wise loss function이 효과적임을 의미합니다. Recall의 경우에도 DAGAD의 성능이 월등한데, normal node로 misclassify되는 anomaly의 비율이 훨씬 적다는 것을 알 수 있습니다. Precision의 경우 다른 detector의 성능이 더 좋지만, 이를 위해 recall이 희생됐다고 해석할 수 있습니다.

2. Comparison with Unsupervised Detectors

image image

위의 차트와 표에서 각각 ROC-curve와 AUC-score를 확인할 수 있습니다. BlogCatalog와 Flickr dataset에서는 월등히 높은 성능, ACM dataset에서는 상위권의 성능을 보입니다.



Ablation Study (Q2, Q3)

Data augmentation module과 Imbalance-tailored learning module의 기여도를 확인하기 위해 앞서 소개한 3개의 dataset에 4개의 DAGAD variant에 대한 실험을 하였습니다.

  • $\mathrm{DAGAD-GCN_ {-IMB} ^ {-AUG}}, \mathrm{DAGAD-GAT_ {-IMB} ^ {-AUG}}$는 두 module 모두 제외합니다. 즉 augmented sample 없이, 그리고 instance-wise CE loss로 학습합니다.
  • $\mathrm{DAGAD-GCN_ {-IMB}}, \mathrm{DAGAD-GAT_ {-IMB}}$는 imbalance-tailored learning module을 제외합니다.

image

위 표에서 볼 수 있듯이, module이 하나 또는 2개 모두 제외된 variant에 비해 원본이 월등히 성능이 높습니다. 따라서 data augmentation module과 imbalance-tailored learning module 모두 anomaly detection performance에 효과적으로 기여한다고 할 수 있습니다.



Sensitivity to Hyper-Parameters (Q4)

Eq. (15)에서 $\alpha, \beta$의 값이 $C_ a, C_ b$ 각각의 training loss의 균형을 맞추는 데 중요한 역할을 한다는 것을 확인할 수 있습니다. 따라서 DAGAD가 두 parameter에 얼마나 sensitive한지 알아보기 위해, BlogCatalog dataset에서 값을 바꿔가며 결과를 뽑았습니다. 이때 $\alpha \in {1.0, 1.2, 1.4, 1.5, 1.6, 1.8, 2.0}, \beta \in {0.1, 0.3, 0.5, 0.7, 0.9, 1.1}$입니다.

image

가장 결과가 좋은 $\alpha, \beta$ 값은 각각 1.6, 0.9 근처임을 확인할 수 있습니다.



5. Conclusion

Summary

이 논문에서는 Graph Anomaly Detection에서 흔히 문제가 되는 anomalous sample scarcity와 class imbalance 문제를 다루었습니다. 소개된 DAGAD 모델은 각각 data augmentation을 통한 sample generation과 class-wise loss function을 통해 두 문제를 해결하려 합니다. 널리 쓰이는 3개의 real-world dataset에 대해 여러 metric에서 10개의 baseline과의 비교를 통해 성능이 높음을 확인할 수 있습니다. 앞으로 class-imbalanced data에서의 발전이 기대가 됩니다.



생각 및 발전 방향

Anomaly에 해당하는 sample의 개수가 너무 부족하다는, 단순하지만 치명적인 문제에 접근해 해결책을 찾으려 시도한 점이 인상 깊었습니다. 주로 몇 개 없는 sample에서 어떻게든 정보를 더 얻으려 하는 다른 method에 비해, 그저 있는 정보를 잘 짜깁기하여 생성한 sample을 추가한 DAGAD가 성능이 훨씬 좋은 것이 흥미로웠습니다. 글도 읽기 쉽게 쓰여 있어 이해하기 어렵지 않은 논문이었습니다.

다만 몇 가지 의문점이 있습니다. 가장 먼저 논문에서 제기한 두 가지 문제, 즉 anomaly의 ‘절대적인’ 개수가 부족하다는 점과 normal node와 비교했을 때의 ‘상대적인’ 개수가 부족하다는 점이 과연 별개의 문제로 취급될 만한지 궁금합니다. 어떻게 보면 결국 같은 말이니까요.

위 의문점의 연장선으로, data augmentation module에서 왜 normal sample도 추가로 생성하는지 의아합니다. 논문에서의 설명대로라면 anomaly sample이 2배, normal sample도 2배로 늘어나는 것인데 이러면 결국 비율은 그대로이기 때문에 class imbalance는 해결되지 않는 것으로 보입니다. 물론 뒤의 imbalance-tailored learning module에서 class imbalance는 따로 다루지만, 이왕 생성하는 김에 anomaly만 더 생성해 애초에 비율을 늘리고 넘어가면 성능이 더 향상되지 않았을까 싶습니다.

마지막으로 hyper-parameter sensitivity analysis에서 왜 $\alpha, \beta$의 범위(1 - 2 vs 0 - 1)이 다른지 궁금합니다. 식에 넣으면 무조건 $C_ a$의 loss가 훨씬 중요하게 작용하는데, fair한 실험인지 의문입니다.

위 의문점을 해소하면서 실험하는 것도 괜찮은 발전 방향인 것 같습니다.

Thank you for reading!



Author Information