CALIBRATING TRANSFORMERS VIA SPARSE GAUSSIAN PROCESSES

0. Summary

Transformer에서 Multi-head attention blocks (MHAs)가 uncertainty calibration을 하지 못하는 점을 지적하며 이것의 output space에서 직접적으로 베이지안 추론을 할 수 있는 Sparse Gaussian Process Attention (SGPA) 라는 개념을 처음으로 제안하였음.

1. Introduction

MHA의 구조를 가진 Transformers는 다양한 분야에서 성공적으로 사용되지만, calibrated uncertainty quantification(UQ)에 대해서는 많이 다루어 지지 않고 있었다. UQ에서는 베이지안 추론이 가장 강력한 방법론 중 하나이고, 다양한 뉴럴네트워크 모델에서 이미 UQ를 위해 사용 되어왔다. 그러한 베이지안 방법론 중 Gaussian Process (GP)는 reliable function-space uncertainty estiamtes에서는 가장 많이 쓰이는 방법론이기 때문에, 이 논문에서는 SGPA 방법론을 제안하는 것이다.

이 논문의 핵심적인 contribution 은 (1) kernel-based attention 이 posterior mean of an sparse variational GP(SVGP)와 동치 관계에 있기 때문에, SGPA를 사용한 Transformer은 deep kernel 이 각각의 GP layer에 사용된 sparse deep GP라고 생각이 될 수 있고 (2) naive extension of SVGP 의 계산 비효율성을 해결하였고 (3) 실험적으로 in-distribution calibration, (out-of-distribution) OOD robustness, 그리고 OOD detection 에서 다른 모델보다 좋은 성능을 보였다.

2. Preliminaries

2.1 Multi-Head Self-Attention(MHSA)

$T$ 개의 queries $\boldsymbol{q} \in \mathbb{R}^{T \times d_q}$, keys $\boldsymbol{k} \in \mathbb{R}^{T \times d_k}\left(d_k=d_q\right)$ 그리고 values $\mathbf{v} \in \mathbb{R}^{T \times d_v}$ 에 대해서, dot-product attention 은 nonlinear activation 함수 $\omega$에 대해 다음과 같이 계산이 된다. $\boldsymbol{F}=\omega\left(\boldsymbol{q} \boldsymbol{k}^{\top}\right) \mathbf{v}$. MHSA는 이러한 self-attention block 을 H개 합친 것이라 이해할 수 있다. Input 에 대해 key, queries, values 에 각각 projection matrix를 사용하여 값을 구해서 최종적으로 다음의 값을 구한다:

$\boldsymbol{F}=\operatorname{concat}\left(\boldsymbol{F}_1, \cdots, \boldsymbol{F}_H\right) \boldsymbol{W}_F$.

2.2 Sparse Variational Gaussian Process(SVGP) with Deep Kernel

GP는 infinite-dimensional index set $\mathcal{X}$의 함수 $f$에 대한 분포이다. 베이지안 추론의 관점에서, GP prior over $f$는 mean function(주로 0으로 set) 과 kernel function($K_\psi(\cdot, \cdot)$)으로 나타낸다.

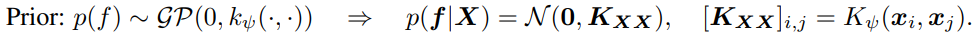
학습 데이터 $(\boldsymbol{X}, \boldsymbol{y})$와 Gaussian likelihood $p(\boldsymbol{y} \mid \boldsymbol{f})=\mathcal{N}\left(\boldsymbol{f}, \sigma^2 \boldsymbol{I}\right)$ 에 대해 새로운 데이터 $\boldsymbol{X}^*$ posterior predictive distribution 은 다음과 같이 표현된다:

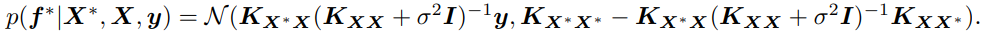
하지만, Gaussian 이 아닌 다른 likelihood 를 사용하거나 데이터 개수 N 이 너무 클때 scalable 하지 않기 때문에 SVGP 방법론을 많이 쓴다. M 개의 inducing variables \((\boldsymbol{Z}, \boldsymbol{u})=\left\{\left(\boldsymbol{z}_m, u_m\right)\right\}_{m=1}^M\)을 사용하여 approximate posterior process 를 다음과 같이 표현할 수 있다:

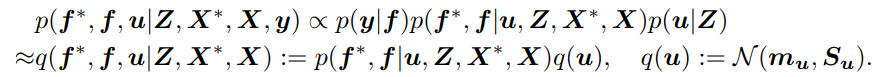
variational parameters를 학습하기 위해서는 evidence lower-bound(ELBO)를 다음과 같이 구해서 계산한다:

\(\mathcal{L}_{E L B O}=E_{q(\boldsymbol{f} \mid \boldsymbol{X}, \boldsymbol{Z})}[\log p(\boldsymbol{y} \mid \boldsymbol{f})]-K L(q(\boldsymbol{u}) \| p(\boldsymbol{u} \mid \boldsymbol{Z}))\).

그리고 나서 approximate posterior predictive distribution 은 다음과 같이 구할 수 있다:

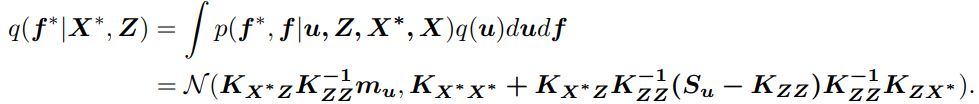
3. Method

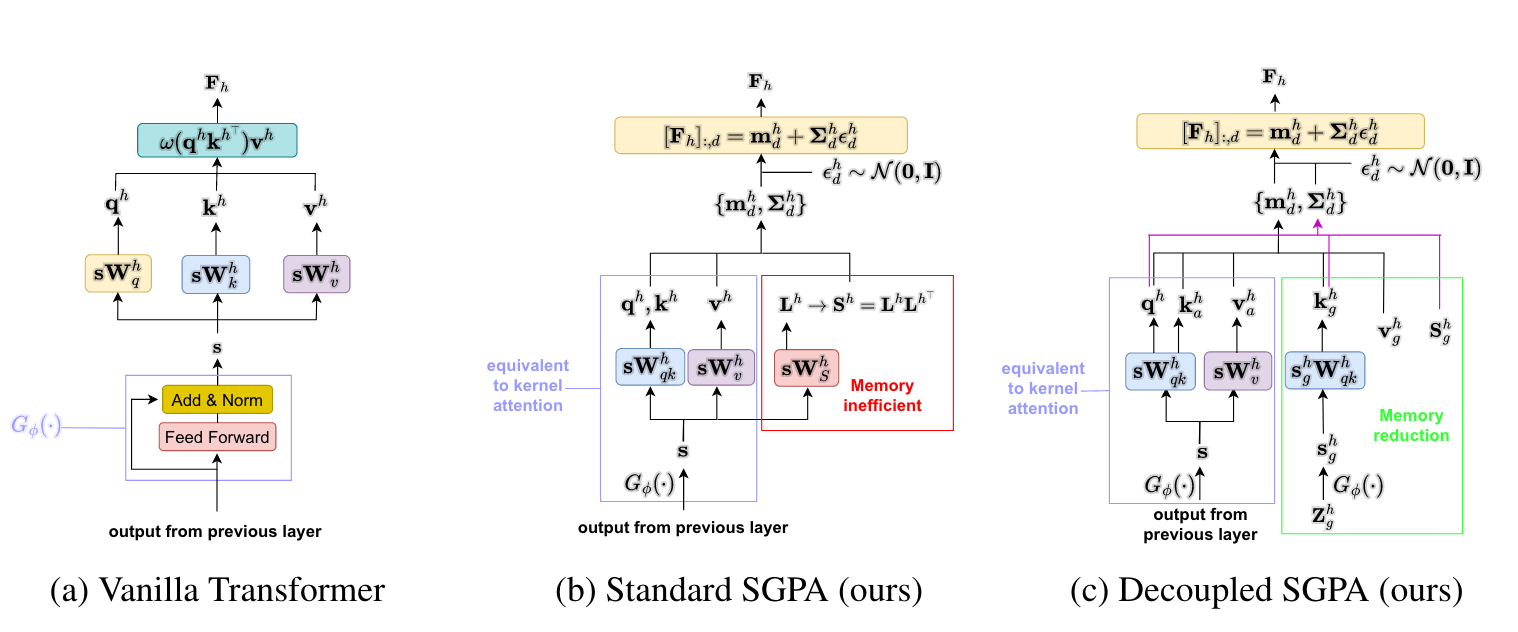
Sparse Gaussian Process Attention(SGPA)의 메인 아이디어는 scaled dot-product attention 을 kernel 로 대체하면서 SGPA 의 평균과 attention 을 연결하는 것이다.

3.1 Attention as the mean of a sparse variational GP

통상적인 Transformers 의 attention block 은 scaled dot-product(SDP) attention 으로 SDP-Attention:

$\quad \boldsymbol{F}=\operatorname{softmax}\left(\frac{\boldsymbol{q} \boldsymbol{k}^{\top}}{\sqrt{d_k}}\right) \mathbf{v}$

으로 표현된다. 이 과정에서 softmax 안은 사실 $\boldsymbol{q}, \boldsymbol{k}$ 사이의 유사성을 찾는 과정이기 때문에, kernel gram matrix \(\boldsymbol{K}_{\boldsymbol{q} \boldsymbol{k}}\left(\left[\boldsymbol{K}_{\boldsymbol{q} \boldsymbol{k}}\right]_{i, j}=K\left(\boldsymbol{q}_i, \boldsymbol{k}_j\right)\right)\) 으로 나타낼 수 있다. 즉, 이러한 kernel attention (K-Attention)은

$K$-Attention: $\quad \boldsymbol{F}=\boldsymbol{K}_{\boldsymbol{q} \boldsymbol{k}} \mathbf{v}$

이렇게 표현이 된다. 이때, $\mathbf{v}$의 각각의 차원에 대 \([\mathbf{v}]_{:,d} :=\boldsymbol{K}_{Z Z}^{-1} \boldsymbol{m}_{\boldsymbol{u}}\)라 하고, $q:=X, k:=Z$로 두면, SVGP posterior mean과 each dimension of the output of a kernel attention block 이 같게 된다.

3.2 Standard SGPA & Its Inefficiency for Self-Attention

위의 동치 관계를 보고, approximate posterior variance computations 에 SVGP 를 사용해 볼 수 있다. 각각의 attention output 의 dimension 에 따라 서로 다른 variational parameters 를 주기 위해 $\boldsymbol{S} \in \mathbb{R}^{T \times T \times d_v}$ 를 a set of variational covariance parameters 라 정의하고 (T는 keys/inducing inputs의 개수), posterior attention output 의 평균과 분산을 다음과 같이 한다:

\(\boldsymbol{m}_d=\boldsymbol{K}_{q k}[\mathbf{v}]_{:, d}, \quad \boldsymbol{\Sigma}_d=\boldsymbol{K}_{q \boldsymbol{q}}+\boldsymbol{K}_{q k}\left(\boldsymbol{K}_{k k}^{-1}[S]_{:,:, d} \boldsymbol{K}_{k \boldsymbol{k}}^{-\mathbf{1}}-\boldsymbol{K}_{k \boldsymbol{k}}^{-\mathbf{1}}\right) \boldsymbol{K}_{k q}\).

이것을 standard SGPA라 부른다. 즉, 각각의 dimension, $d$,들이 같은 kernel 을 공유하지만 서로 다른 variational parameters 를 사용한다는 것이 중요하다. 하지만, 이는 computationally inefficient 한 방법이다. 쉽게 생각해서, covariance parameter 이 input 과 inducing variable 에 dependent 해야한다.

3.1 Improving Time & Memory Efficiencies via Decoupled SGPA

이러한 문제를 “orthogonally decoupled sparse Gaussian process approximation”을 통해서 해결하고자 한다. Input-dependent 한 (amortised) keys/inducing inputs, $\boldsymbol{k}^h_a=s \boldsymbol{W}_k^h$, 에 더해, $M_g$ 개의 “global” keys/inducing inputs, $\boldsymbol{k}^h_g$,를 모든 input sequences 들이 공유한다. 메인 아이디어는, 이 global keys 들만으로 variance of sparse GP 를 계산해 효율성을 개선하고자하는 것이다. 즉, 이렇게 하면 $\boldsymbol{S}^h$가 input-independent 해도 된다. 이것에 의하면, 각각의 head 에 대한 각각의 dimension 에 대한 mean, covariance 는 다음과 같다:

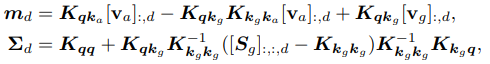
\(\mathbf{v}_g \in \mathbb{R}^{M_g \times d_v}, \boldsymbol{S}_g \in \mathbb{R}^{M_g \times M_g \times d_v}$ 그리고 $\mathbf{v}_a=s \boldsymbol{W}_v \in \mathbb{R}^{T\times d_v}\). 이것을 decoupled SPGA 라 부른다.

Model	Time	Additional Memory
MLE	$O\left(B T^2\right)$	-
Standard SGPA	$O\left(B T^3\right)$	$O\left(T^2\right)$
Decoupled SGPA	$O\left(B T^2M_g + M_g^3\right)$	$O\left(M_g^2\right)$

3.4 Transformer Based on Decoupled SGPA

SGPA 가 Sparse GP 랑 같기 때문에, Transformer model 을 각각의 layer 에 deep kernel 이 있는 deep GP 의 sparse approximation 이라 생각할 수 있다. 전체적인 구조는 우리가 잘 알고있는 Transformer 과 유사하다: $l$th SGPA layer 의 input 은 $l-1$th SGPA의 output, $\boldsymbol{F}^{l-1} \in \mathbb{R}^{T \times d^{l-1}}$, 이고 우선 non-linear mapping, $G_{\phi^l}: \mathbb{R}^{d^{l-1}} \rightarrow \mathbb{R}^{d^l}$,을 한 후 다음을 계산한다.

\(\boldsymbol{q}^{l, h}=\boldsymbol{k}_a^{l, h}=G_{\phi^l}\left(\boldsymbol{F}^{l-1}\right) \boldsymbol{W}_{q k}^{l, h}, \quad \boldsymbol{k}_g^{l, h}=G_{\phi^l}\left(\boldsymbol{Z}_g^{l, h}\right) \boldsymbol{W}_{q k}^{l, h}, \quad \mathbf{v}_a^{l, h}=G_{\phi^l}\left(\boldsymbol{F}^{l-1}\right) \boldsymbol{W}_v^{l, h}\),

$\boldsymbol{Z}_g^{l, h} \in \mathbb{R}^{M_g \times d^{l-1}}$ 은 global inducing locations of the $l$th layer이다. 그리고, variational parameters, $\left(\mathbf{v}_g^{l, h}, \boldsymbol{S}_g^{l, h}\right)$, 을 통해 posterior attention output 의 평균과 공분산을 구한 후, uncertainty propagation 을 위해 reparameterization trick 을 사용해

\(\left[\boldsymbol{F}_h^l\right]_{:, d}=\boldsymbol{m}_d^{l, h}+\boldsymbol{\Sigma}_d^{l, h} \boldsymbol{\epsilon}_d^{l, h}, \quad \boldsymbol{\epsilon}_d^{l, h} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})\).

와 같이 전달 한다. 그리고 나서 최종적으로는 아래의 ELBO 를 학습시킨다:

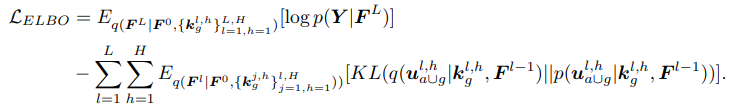
실제 실험에서는, Monte-Carlo 방법을 통해 이 값을 추정한다.

4. Experiment

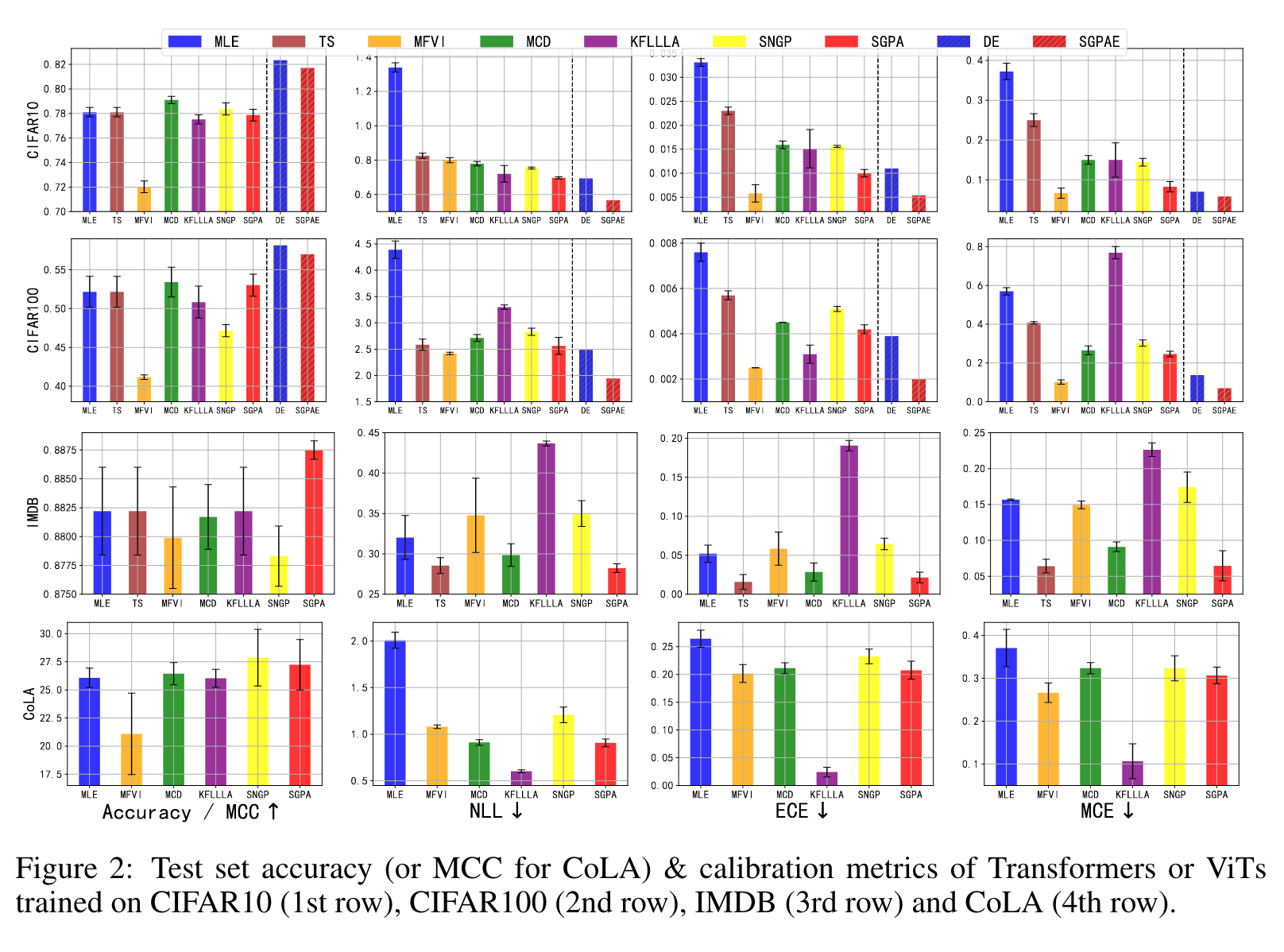
다음과 같은 setup 으로 실험을 진행하였다.

• 데이터 : CIFAR10&CIFAR100 (CV), CoLA (NLP), IMDP (NLP)
• Network 구조 : CV 문제에는 Vision Transformers 사용함. Kernel attention 에는 NLP 에는 exponential kernel, CV 에는 ARD-RBF kernel 사용함.
• Baselines : Maximum likelihood estimation (MLE), Bayesian inference methods including mean-field variational inference (MFVI), Monte-Carlo Dropout (MCD), Kronecker-factored last layer Laplace approximation (KFLLLA), Spectral-normalized Neural Gaussian Process (SNGP). Validation set 이 있는 문제의 경우 temperature scaling (TS)를 사용해 calibration set 으로서 활용. CV 문제에 대해서는 ensemble 도 고려해 SGPA ensemble (SGPAE) with deep ensemble (DE).
• Evaluations & Metrics: 이 세가지를 보았음 in-distribution performance, out-of-distribution (OOD) robustness and OOD detection. 그 외 test set 에서는 다양한 metric 으로 측정하고 5개의 독립적인 run 을 통해 mean +/- two sigma 로 기록하였음.

4.1 In-distribution Calibration

모든 “single model” calibration 이 in-distribution calibration 을 향상시켰다. MFVI 는 가장 낮은 calibration errors 를 갖고 있지만, underfitting 이 보인다. 전반적으로 4가지 데이터셋에서 모두 SGPA 가 다른 single-model baseline 보다 좋은 성능을 보이며 competitive predictive accuracy 도 보였다.

4.2 Robust Prediction on Out-of-distribution

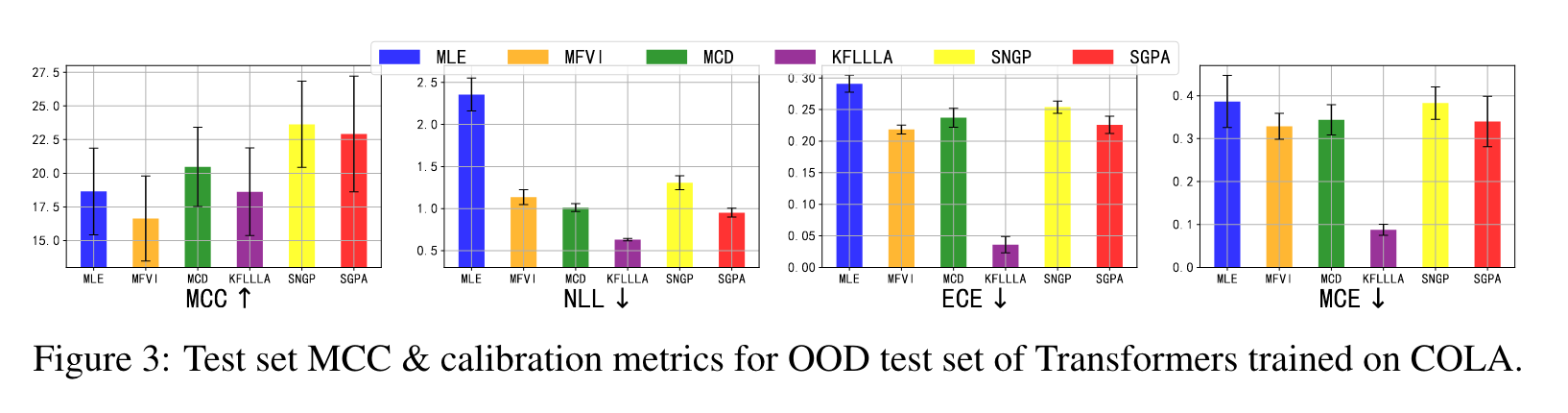
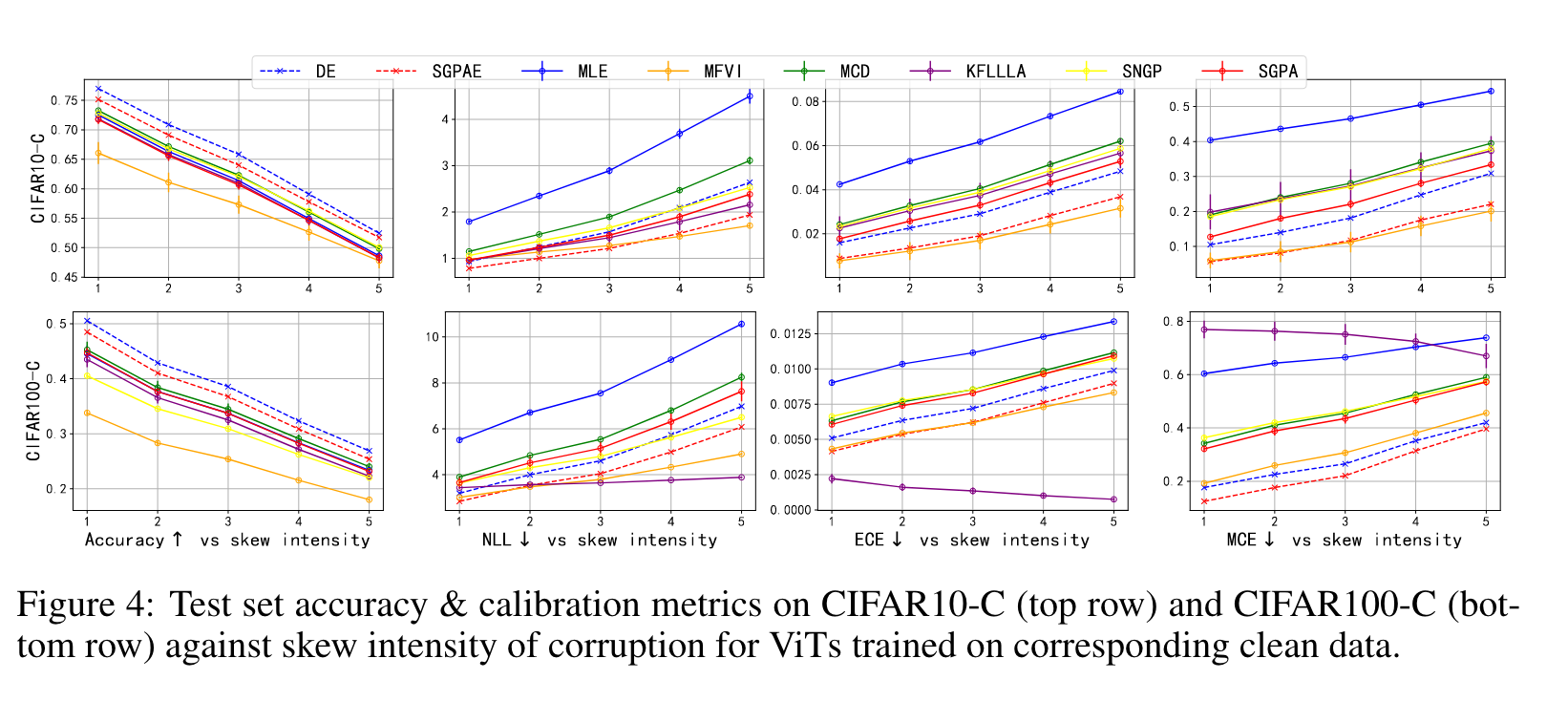
CoLA 와 이미지 분류 문제인 CIFAR10&CIFAR 100 에서 distribution shift 가 있을때의 성능을 분석하였다. 기존의 다른 연구에서 나온 OOD 데이터를 기반으로 실험을 하였을때, SGPA 는 MLE, MCD, SNGP를 NLL, calibration errors 측면에서 향상된 성능을 보였으면서 더욱 좋은 정확도를 보였다. MFVI, KFLLLA 는 더 낮은 calibration error 를 보였지만, predictive accuracy 가 좋지 못했다. OOD robustness 에 대해서도 실험을 했을 때 이와 같은 결과가 나왔다.

4.3 Out-of-distribution Detection

이미지 분류 데이터에 학습된 Transformer 에 대해 OOD detection 문제를 비교해보았다. 전반적으로 다른 베이스라인 모델들보다 SGPA 가 랭크가 높았으며, ensemble 을 이용한 SGPAE 가 그중 가장 좋은 성능을 보였다.

5. Conclusion

SGPA를 제안하며 attention blocks 의 output 에 대해 approximate Bayesian inference 를 할 수 있는 방법론을 제안하였다. 다른 베이스라인에 비해 predictive accuracy 와 calibration 사이의 balance 가 훨씬 좋은 결과를 가져오게 되었다. 추가적으로 이러한 uncertainty quantification 을 잘하는 것은 distribution shift 하에서도 robustness 를 보였고, out of distribution detection 에서도 강점을 보였다.

---

Author Information

• Joohwan Ko
  • Masters student at Industrial Systems and Engineering, KAIST
  • Bayesian Machine Learning, Stochastic Optimization

6. Reference & Additional materials

• Github Implementation https://github.com/chenw20/SGPA
• Reference
  Wenlong Chen and Yingzhen Li. Calibrating Transformers via Sparse Gaussian Processes. International Conference on Learning Representations (ICLR), 2023.