[SIGIR-24] SelfGNN: Self-Supervised Graph Neural Networks for Sequential Recommendation
1. Introduction and Motivation
Recommender systems play a critical role in modern digital platforms, enabling personalized content delivery on services like Amazon, TikTok, and YouTube. A significant branch of this field is sequential recommendation, which models user-item interactions over time to predict future behaviors. For instance, predicting the next movie a user might watch based on their viewing history. Sequential recommendation hinges on capturing both short-term interests and long-term preferences. However, existing approaches often fall short by focusing on either temporal dynamics (e.g., GRU4Rec, SASRec, and Bert4Rec) or collaborative relationships (e.g., NGCF and LightGCN), neglecting their integration (Hidasi et al. 2016; Kang and McAuley 2018; Liu et al. 2019; Wang et al. 2019; He et al. 2020).
Self-supervised learning (SSL) has emerged as a promising paradigm in recommender systems, leveraging unlabeled data to address challenges like data sparsity. However, SSL-based sequential models often depend heavily on high-quality data, making them vulnerable to noise in real-world user interactions, such as misclicks or temporary intents (Xia et al. 2023).
Liu et al. (2024) address these limitations with SelfGNN, a novel self-supervised framework for sequential recommendation. SelfGNN integrates short-term collaborative relationships and long-term user preferences while mitigating noise through personalized self-augmented learning. By effectively encoding and denoising interaction sequences, SelfGNN sets a new standard for robust and accurate sequential recommendations.
2. Preliminary
2.1 Message Passing
Message Passing is the central process of Graph Convolution Networks (GCN) in order to encode graph structural information (Kipf and Welling 2017). The core idea is to send messages of information between the nodes to iteratively update the encoded node representations. Specifically, Liu et al. were inspired by LightGCN (He et al. 2017) where each user-node $\boldsymbol{e}_ {u}^{(k)}$ and item-node $\boldsymbol{e}_ {i}^{(k)}$ encoding are updated by the weighted sum of their neighboring nodes:
$ \boldsymbol{e}_ {u}^{(k+1)} = \sum_ {i\in\mathcal{N}_ u} \frac{1}{\sqrt{\vert\mathcal{N}_ u\vert}\sqrt{\vert\mathcal{N}_ i\vert}}\boldsymbol{e}_ {i}^{(k)} $
$ \boldsymbol{e}_ {i}^{(k+1)} = \sum_ {u\in\mathcal{N}_ i} \frac{1}{\sqrt{\vert\mathcal{N}_ i\vert}\sqrt{\vert\mathcal{N}_ u\vert}}\boldsymbol{e}_ {u}^{(k)} $
Where $\boldsymbol{e}_ {u}^{(0)}$ and $\boldsymbol{e}_ {i}^{(0)}$ are the initial ID embedding for the user and item respectively.
2.2 Self-Attention
Another key operation for propagating information, which has gained significant popularity in graph-based learning, is self-attention (Vaswani et al. 2017). Self-attention is particularly effective at capturing relationships in temporal or sequential data due to its ability to focus on relevant parts of the input sequence, regardless of their position.
The core idea of self-attention is to project the input matrix $\boldsymbol{X} \in \mathbb{R}^{n \times d}$ into the query, key, and value subspaces using learnable projection matrices $\boldsymbol{W}_ Q \in \mathbb{R}^{d \times d_ Q}$, $\boldsymbol{W}_ K \in \mathbb{R}^{d \times d_ K}$, and $\boldsymbol{W}_ V \in \mathbb{R}^{d \times d_ V}$, respectively (where $d_ K = d_ Q$). These projections allow the model to compare elements of the input sequence and determine which parts to focus on.
The (single-head) attention is then computed as:
$ \text{Attn}(\boldsymbol{X}) = \text{Softmax}\left(\frac{\boldsymbol{XW}_ {Q}(\boldsymbol{XW}_ K)^\mathsf{T}}{\sqrt{d_ K}}\right)\boldsymbol{XW}_ V = \text{Softmax}\left(\frac{\boldsymbol{QK}^\mathsf{T}}{\sqrt{d_ K}}\right)\boldsymbol{V} $
By learning dynamic weights through attention, this mechanism excels at modeling long-range dependencies and temporal relationships, making it well-suited for sequential and temporal data such as sequential recommendation, where contextual relevance across time steps is critical.
2.3 Validation Metrics
To validate the effectiveness of their proposed method they used the Hit Rate (HR)@N and Normalized Discounted Cumulative Gain (NDCG)@N where the Hit Rate at $N$ is the fraction of users whose top $N$ recommendations include at least one relevant item.
To calculate the Normalized Discounted Cumulative Gain, we first calculate the Discounted Cumulative Gain (DCG) and then normalize it using the Idealized discounted cumulative gain (IDCG). For a user with predicted item ranking-position order $p_ i$ and ground-truth item-relevance $r_ i$ DCG@N is computed as:
$ DCG@N = \sum_ {i = 1}^N \frac{r_ i}{\log (p_ {i} +1)} $
The idea of NDCG is to normalize the DCG with the ideal discounted cumulative gain (IDCG). The equation for IDCG is almost equivalent to that of DCG, however, we just assume that the item positions $p_ i$ are ordered according to their relevance $r_ i$. This way, the IDCG represents the best possible ranking order the recommender could produce. With this in mind, the final equation for NDCG is:
$ NDCG@N = \frac{DCG@N}{IDCG@N} = \frac{\sum_ {i = 1}^N \frac{r_ i}{\log (p_ i +1)}}{\sum_ {i = 1}^N \frac{r_ i}{\log (p’_ {i} +1)}} \in [0,1] $
In the paper, they set $N = \lbrace 0,20 \rbrace$ for both HR@N and NDCG@N.
3. Method
Given the set of users $\mathcal{U} = \lbrace u_ 1,\dots, u_ I\rbrace$ with $\vert\mathcal{U}\vert = I$ and the set of items, $\mathcal{V} = \lbrace v_ i,\dots,v_ J\rbrace$ where $\vert\mathcal{V}\vert = J$ the time-dependent adjacency matrix $\boldsymbol{\mathcal{A}}_ {t} \in\mathbb{R}^{I\times J}$ represents the user-item interaction at time $t$. Here, the time $t$ is discretized by the hyperparameter $T$ such that each time interval has length $(t_ e - t_ b)/T$ where $t_ b$ and $t_ e$ are the first (beginning) and last (end) observed time stamp. Thus in other words, ${\mathcal{A}}_ {t,i,j}$ is set to 1 if user $u_ i$ interacted with item $v_ j$ at time $t$. Then, giving $\lbrace \boldsymbol{\mathcal{A}}_ {t}| 1\leq t \leq T\rbrace$ the objective is to predict future user-item interactions $\boldsymbol{\mathcal{A}_{T+1}}$. Formally, they define the objective as:
$ \arg\min_ {\Theta_ f,\Theta_ g} \mathcal{L}_ {recom}\left(\boldsymbol{\mathcal{\hat{A}}_ {T+1}},\boldsymbol{\mathcal{A}_ {T+1}}\right) + \mathcal{L}_ {SAL}(\boldsymbol{E}_ s,\boldsymbol{E}_ l) $
$ \boldsymbol{\mathcal{\hat{A}}_ {T+1}} = f\left(\boldsymbol{E}_ s,\boldsymbol{E}_ l\right)\quad \boldsymbol{E}_ s,\boldsymbol{E}_ l = g(\lbrace\boldsymbol{\mathcal{A}}_t\rbrace) $
Where $\mathcal{L}_ {recom}$ is the recommendation error between the true and predicted user-item interactions $\boldsymbol{\mathcal{A}_ {T+1}}$ and $\boldsymbol{\mathcal{\hat{A}}_ {T+1}}$, respectively. $\mathcal{L}_ {SAL}$ is the self-augmentation learning (SAL) loss which uses the long and short-term embeddings $\boldsymbol{E}_ l,\boldsymbol{E}_ s$ which are encoded using the sequential data and encoder $g$. Lastly, the estimated predictions $\boldsymbol{\mathcal{\hat{A}}_ {T+1}}$ is also calculated using these embeddings and prediction function $f$.
3.1 Encoding Short-term user-item interactions
The model begins by modeling the short-term interactions, which are essential to the encoding process. Inspired by LightGCN (He et al. 2017), they project each user $u_ i$ and item $v_ j$ for each timestep $t$ into a $d$-dimensional latent space using their IDs. These embeddings $\boldsymbol{e}_ {t,i}^{(u)}$, $\boldsymbol{e}_ {t,j}^{(v)}$ are assembled to the embedding matrices $\boldsymbol{E}_ t^{(u)}\in\mathbb{R}^{I\times d}$,$\boldsymbol{E}_ t^{(v)} \in\mathbb{R}^{J\times d}$ which are then updated through the following message passing method:
$ \boldsymbol{z}_ {t,i}^{(u)} = \text{LeakyReLU} \left( \mathcal{A}_ {ti,{*}} \cdot \boldsymbol{E}_ t^{(v)}\right), \quad \boldsymbol{z}_ {t,j}^{(v)} = \text{LeakyReLU} \left( \mathcal{A}_ {tj,{*}} \cdot \boldsymbol{E}_ t^{(u)} \right) $
This is repeated for $L$-layers with the embeddings in the $l$-th layer defined as:
$ \boldsymbol{e}_ {t,i,l}^{(u)} = \boldsymbol{z}_ {t,i,l}^{(u)}+\boldsymbol{e}_ {t,i,l-1}^{(u)},\quad \boldsymbol{e}_ {t,i,l}^{(v)} = \boldsymbol{z}_ {t,i,l}^{(v)}+\boldsymbol{e}_ {t,i,l-1}^{(v)} $
Finally, all embeddings for each layer are concatenated together to form the final short-term embeddings $\boldsymbol{e}_ {t,i}^{(u)}$ and $\boldsymbol{e}_ {t,j}^{(v)}$:
$ \boldsymbol{e}_ {t,i}^{(u)} = \boldsymbol{e}_ {t,i,1}^{(u)}| \dots| \boldsymbol{e}_ {t,i,L}^{(u)},\quad\boldsymbol{e}_ {t,j}^{(v)} = \boldsymbol{e}_ {t,j,1}^{(v)}| \dots| \boldsymbol{e}_ {t,j,L}^{(v)} $
3.2 Encoding Long-term user-item Interactions
The long-term user-item information is encoded in two different ways, which are combined for the final prediction in the end. First, they introduce Interval-Level Sequential Pattern Modeling which aims to capture dynamic changes from period to period by integrating the aforementioned short-term embeddings into long-term embeddings using temporal attention. Second, they define Instance-Level Sequential Pattern Modeling which learns the pairwise relations between specific item instances directly (Liu et al. 2024).
Interval-Level Sequential Pattern Modeling To integrate short-term embeddings into long-term ones they use the Gated Recurrent Unit (GRU) (Cho et al. 2014) on the sequential short-term embeddings $\lbrace\boldsymbol{e}_ {t,i}^{(u)}\rbrace$ and $\lbrace\boldsymbol{e}_ {t,j}^{(v)}\rbrace$ for each user $u_ i$ and item $v_ j$. More specifically, each hidden state $\boldsymbol{h}_ {t,i}^{(u)}$ and $\boldsymbol{h}_ {t,j}^{(v)}$ of the GRU model is collected to interval-level sequences $S_ i^{interval}$ and $S_ j^{interval}$:
$ S_ i^{interval} = \left(\boldsymbol{h}_ {1,i}^{(u)},\dots,\boldsymbol{h}_ {T,i}^{(u)}\right),\quad S_ j^{interval} = \left(\boldsymbol{h}_ {1,j}^{(v)},\dots,\boldsymbol{h}_ {T,j}^{(v)}\right) $
where:
$ \boldsymbol{h}_ {t,i}^{(u)} = \text{GRU}\left(\boldsymbol{e}_ {t,i}^{(u)},\boldsymbol{h}_ {t-1,i}^{(u)}\right) ,\quad \boldsymbol{h}_ {t,j}^{(v)} = \text{GRU}\left(\boldsymbol{e}_ {t,j}^{(v)},\boldsymbol{h}_ {t-1,j}^{(v)}\right) $
Then (multi-head dot-product) self-attention is applied for the interval-level sequences to uncover the temporal patterns:
$ \boldsymbol{\bar H}_ i^{(u)} = \text{Self-Att}\left(S_ i^{interval} \right),\quad \boldsymbol{\bar H}_ j^{(v)} = \text{Self-Att}\left(S_ j^{interval} \right), $
Which finally, are summed across time:
$ \boldsymbol{\bar e}_ i^{(u)} = \sum_ {t=1}^T \boldsymbol{\bar H}_ {i,t}^{(u)},\quad \boldsymbol{\bar e}_ j^{(v)} = \sum_ {t=1}^T \boldsymbol{\bar H}_ {j,t}^{(v)} $
Where $\boldsymbol{\bar e}_ i,\boldsymbol{\bar e}_ j\in\mathbb{R}^{d}$ is final the long-term (interval-level) embeddings for user $u_ i$ and item $v_ j$. Note that while short-term embeddings depend on the time interval $t$, long-term embeddings are independent of $t$, as it is effectively integrated out.
Instance-Level Sequential Pattern Modeling However, interval-level embeddings are not the only long-term embeddings used in the SelfGNN. The model also uses instance-level sequential patterns by applying self-attention directly over sequences containing users’ interacted item instances. Given a user $u_ i$ they denote the $m$’th interacted item for that user as $v_ {i,m}$ for $m = \lbrace 1,\dots,M\rbrace$ (for a set maximum interaction length $M$). Then the sequences of items user $u_ i$ interacted with can be modeled as:
$ S_ {i,0}^{instance} = \left(\boldsymbol{\bar e}_ {v_ {i,1}}^{(v)}+ \boldsymbol{p}_ 1,\dots,\boldsymbol{\bar e}_ {v_ {i,M}}^{(v)} + \boldsymbol{p}_ M\right) $
Where $\boldsymbol{\bar e}_ {v_ {i,m}}^{(v)} \in\mathbb{R}^d$ is the aforementioned long-term embedding for item $v_ {i,m}$ and $\boldsymbol{p}_ m\in\mathbb{R}^d$ is learnable position embeddings for the $m$-th position. Then $L_ {attn}$ layers of self-attention (with residual connections) are applied on the instance-level sequence $S_ {i,0}^{instance}$:
$ S_ {i,l}^{instance} = \text{LeakyReLU}\left(\text{Self-Attn}\left(S_ {i,l-1}^{instance}\right)\right) + S_ {i,l-1}^{instance} $
The final instance-level embedding is calculated by summing over the elements of the final sequence $S_ {i,L_ {attn}}^{instance}$:
$ \boldsymbol{\tilde e}_ i^{(u)} = \sum S_ {i,L_ {attn}}^{instance} $
Predicting Future user-item interactions The prediction for new user-item interactions $\mathcal{\hat A}_ {T+1,i,j}$ for user $u_ i$ and item $v_ j$ is now computed using the long-term embeddings (which implicitly uses the short-term embeddings):
$ \mathcal{\hat A}_ {T+1,i,j} = \left(\boldsymbol{\bar e}_ i^{(u)} + \boldsymbol{\tilde e}_ i^{(u)} \right)^{\mathsf{T}} \cdot \boldsymbol{\bar e}_ j^{(v)} $
They optimize with the following loss function (to prevent predicted values from becoming arbitrarily large):
$ \mathcal{L}_ {recom} \left(\mathcal{A}_ {T+1,i,j},\mathcal{\hat A}_ {T+1,i,j}\right) = \sum_ {i = 1}^I \sum_ {k=1}^{N_ {pr}} \max \left(0,1 -\mathcal{\hat A}_ {T+1,i,p_ {k}} + \mathcal{\hat A}_ {T+1,i,n_ k} \right) $
where $N_ {pr}$ is the number of samples and $p_ k$ and $n_ k$ is the $k$-th positive (user-interaction) and negative (no user-interaction) item index respectively.
3.3 Denoising short-term user-item interactions
While short-term user interactions are important for modeling sequential user-item interaction patterns they often contain noisy data. Here noise refers to any temporary intents or misclicks, which cannot be considered as long-term user interests or recent interests for predictions (Liu et al. 2024). An example of this is when an aunt buys Modern Warfare III for her nephew for Christmas because this interaction does not reflect the user $u_ {aunt}$’s interests. Other examples are simple misclicks or situations where a user clicks on something expecting it to be a different thing. Thus to denoise these noisy short-term user-item interactions they propose to filter them using long-term interactions. Specifically, for each training sample of the denoising SSL, they sample two observed user-item edges $(u_ i,v_ j)$ and $(u_ {i’},v_ {j’})$ from the short-term graphs $\boldsymbol{\mathcal{A}}_ {t}$ and calculate the likelihood $s_ {t,i,j}, \bar{s}_ {i,j}, s_ {t,i’,j’}, \bar{s}_ {i’,j’} \in\mathbb{R}$ that user $u_ i$/$u_ {i’}$ interacts with item $v_ j$/$v _ {j’}$ at time step $t$ and in the long-term, respectively. For $(u_ i,v_ j)$ the likelihoods are ($s_ {t,i’,j’}, \bar{s}_ {i’,j’}$ are calculated in the same way):
$ s_ {t,i,j} = \sum_ {k= 1}^d \text{LeakyReLU}\left(e_ {t,i,k}^{(u)}\cdot e_ {t,j,k}^{(v)}\right),\quad \bar{s}_ {t,i,j} = \sum_ {k= 1}^d \text{LeakyReLU}\left(\bar{e}_ {i,k}^{(u)}\cdot \bar{e}_ {t,j,k}^{(v)}\right) $
Where $e_ {t,i,k}^{(u)},e_ {t,j,k}^{(v)},\bar{e}_ {i,k}^{(u)},\bar{e}_ {t,j,k}^{(v)}\in\mathbb{R}$ are the element values of the $k$-th embedding dimension. Thus the SAL objective functions become:
$ \mathcal{L}_ {SAL} = \sum_ {t=1}^T\sum_ {(u_ {i},v_ {j}),(u_ {i’},v_ {j’})} \max\left(0,1- (w_ {t,i}\bar{s}_ {t,i,j} - w_ {t,i’}\bar{s}_ {t,i’,j’})\cdot (s_ {t,i,j} -s_ {t,i’,j’} )\right) $
With learnable stabilty weigths $w_ {t,i’},w_ {t,i’}\in\mathbb{R}$ calculated using the short and long-term embeddings:
$ w_ {t,i} = \text{Sigmoid}\left(\boldsymbol{\Gamma}_ {t,i} \cdot\boldsymbol{W}_2 + b_2\right) $
$ \boldsymbol{\Gamma}_ {t,i} = \text{LeakyReLU} \left( \left( \boldsymbol{\bar{e}}^{(u)}_ {i} + \boldsymbol{e}^{(u)}_ {t,i} + \boldsymbol{\bar{e}}^{(u)}_ {i} \odot \boldsymbol{e}^{(u)}_ {t,i} \right) \boldsymbol{W}_ {1} + \boldsymbol{b}_ {1} \right) $
With learnable parameters $\boldsymbol{W}_ {1}\in\mathbb{R}^{d\times d_ {SAL}}$, $\boldsymbol{W}_ {2}\in\mathbb{R}^{d_ {SAL}\times 1}$, $\boldsymbol{b}_ {1}\in\mathbb{R}^{d_ {SAL}}$, and ${b}_ {2}\in\mathbb{R}$. Thus the final learning objective becomes:
$ \mathcal{L} = \mathcal{L}_ {recom} + \lambda_ {1}\mathcal{L}_ {SAL} + \lambda_ {2}\cdot \vert \Theta\vert _ F^2 $
For weight-importance parameters $\lambda_1$ and $\lambda_2$. The complete procedure is shown in Figure 1.

Figure 1: Overview of the SelfGNN framework
4. Experiment
4.1 Objective
The primary objective of the experiments was to compare SelfGNN with state-of-the-art models in top-$N$ recommendation. Additionally, an ablation study was conducted to evaluate the impact of removing or altering different model modules. To evaluate the model’s robustness, they performed a separate experiment injecting varying levels of noise into the data. Finally, a case study examined how the model identifies potentially noisy items for a specific user.
4.2 Experiment setup
Data sets The SelfGNN model is tested using an Amazon-book dataset (user ratings of books by Amazon) (He and McAuley 2016), Gowalla dataset (user geolocation check-ins) (Cho et al. 2011), Movielens dataset (users’ ratings for movies from 2002 to 2009)(Harper and Konstant 2015), and Yelp data set (venue reviews sampled from 2009 to 2019) (Liu et al. 2024). Furthermore, the 5-core setting is applied which removes all users and items with less than 5 interactions.
Baselines They test their method against a variety of methods. This includes BiasMF (Koren et al. 2009), NCF (He et al. 2017), GRU4Rec (Hidasi et al. 2016), SASRec (Kang and McAuley 2018), TiSASRec (Li et al. 2020), Bert4Rec (Liu et al. 2019), NGCF (Wang et al. 2019), LightGCN (He et al. 2017), SRGNN (Wu et al. 2019), GCE-GNN (Wang et al. 2020), SURGE (Chang et al. 2021), ICLRec (Chen et al. 2022), CoSeRec(Liu et al. 2021), CoTRec (Xia et al. 2021), and CLSR (Zheng et al. 2022).
Evaluation For evaluation, the data sets were split by time such that the most recent observations were used for testing, the earliest observations were used for training, and the remaining (middle) observations were used for validation. Furthermore, 10.000 users were sampled as test users for which negative samples were created by selecting 999 items the test user had not interacted with. Lastly, they use Hit rate (HR)@N and Normalized Discounted Cumulative Gain (NDCG)@N for $N = \lbrace 10,20\rbrace$ as their evaluation metrics.
4.3 Results
Performance The main results are presented in Figure 2:

Figure 2: Results for the top 10 and top 20 recommendations for the SelfGNN and the baselines
These results confirm that SelfGNN consistently outperforms state-of-the-art baselines across multiple datasets. It demonstrates that the model is successfully able to integrate short-term collaborative patterns with long-term temporal sequences while mitigating the impact of noisy interactions. For example, unlike SASRec and Bert4Rec, which primarily model sequential patterns, or NGCF and LightGCN, which focus on collaborative filtering, SelfGNN bridges these approaches with its personalized self-augmented learning framework. This design enables it to capture user behavior comprehensively and adapt to diverse interaction scenarios, including noisy or sparse environments.
Ablation study The ablation study focuses on the techniques for Short-term Learning, Long-term Learning and Long and Short-term Personalized Self-Augmented Learning. The results are shown in Figure 3.

Figure 3: Module ablation study of the SelfGNN model.
Notably, the performance drop is greatest when the GRU-attention is replaced with a feature fusion method based on summation (-GAT) and when the collaborative filtering is removed (-CF) for long-term learning. This demonstrates the importance of encoding long-term user information using sequential encoders and collaborative filtering. Importantly, SelfGNN demonstrates the highest performance among the ablations.
Injecting Noise To analyze the SelfGNN robustness against noise, they conducted experiments where they injected noise into the data by randomly replacing real item interactions with randomly generated fake ones. Figure 4 shows the performance of the SelfGNN and the top baselines (Surge, CoSeTec, Bert4Rec) on the Amazon and Movielens data set as the percentage of fake items increased.
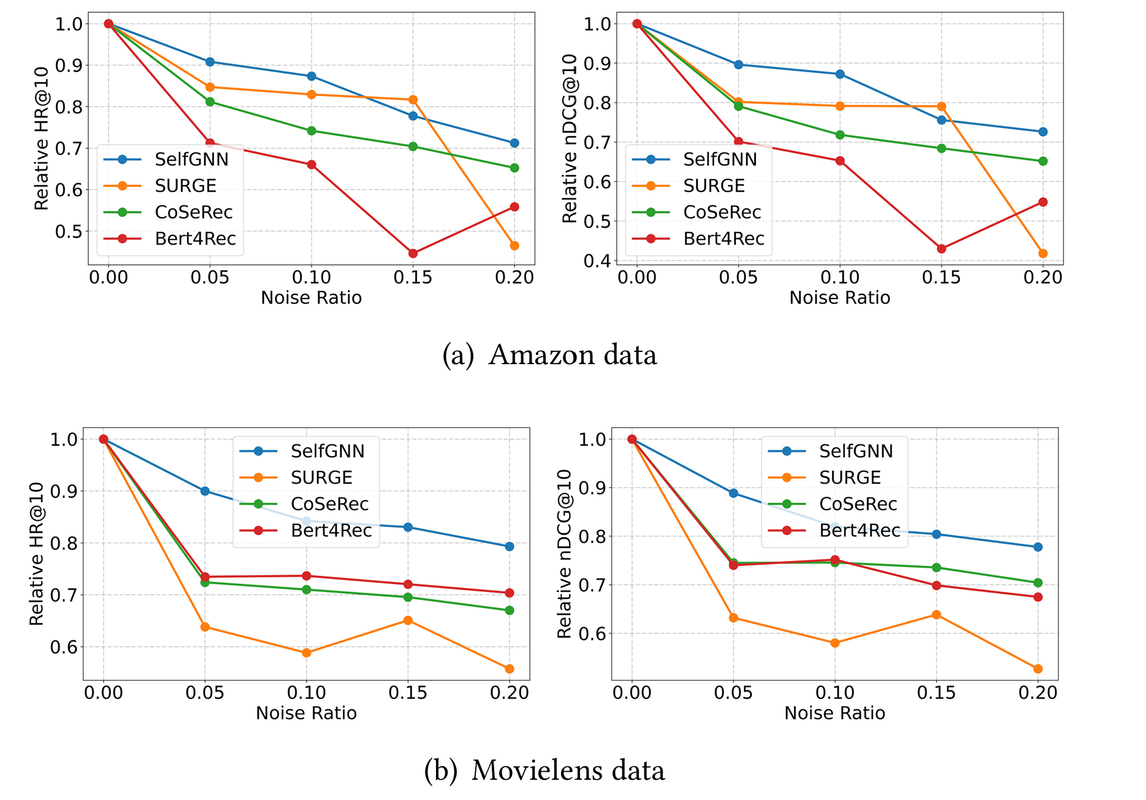
Figure 4: Relative HR@10 as a function of noise ratio for the SelfGNN and top baselines on the Amazon (a) and Movielens (b) data set
From the figure, we observe that performance decreases for all models as noise increases; however, the decline is much slower for SelfGNN, indicating that it is more stable and robust to noise. Notably, the relative HR@10 drop is significantly higher for the other models on the Movielens dataset when only 5% of the data is replaced with noise. Interestingly, the relative performance drop of SURGE for NDCG@10 on the Amazon dataset is slightly less than that of SelfGNN at 15%. However, when noise increases to 20%, the relative performance drop of SURGE becomes the worst among all models. This is likely because the Amazon dataset is sparse, which naturally amplifies the impact of injected noise.
Case Study: Lastly, they examine the effect of personal self-augmentation learning for user-item recommendations. They begin by sampling a user $u_ a$ (6128) and a portion of their item interaction sequence. Then, they randomly select another user $u_ b$ (824) who shares at least 20 item interactions in common with $u_ a$. They calculate the user-item similarity scores $\mathcal{\hat{A}}_ {T+1, i, j}$ for $u_ a$ and the items in their interaction sequence, both with (w-score) and without (wo-score) self-augmented learning (see Figure 5).
Interestingly, the score for item $v_ a$ (6282) drops from 0.8239 to 0.3686 when personal self-augmentation learning is applied. This suggests that the interaction between $u_ a$ and item $v_ a$ may be noise. This hypothesis is supported by the fact that item $v_ a$ belongs to a different category, Mystery, whereas the other items (shown in blue) belong to the Action & Adventure category. Furthermore, user $u_ b$, who shares multiple items with $u_ a$, has not interacted with $v_ a$.
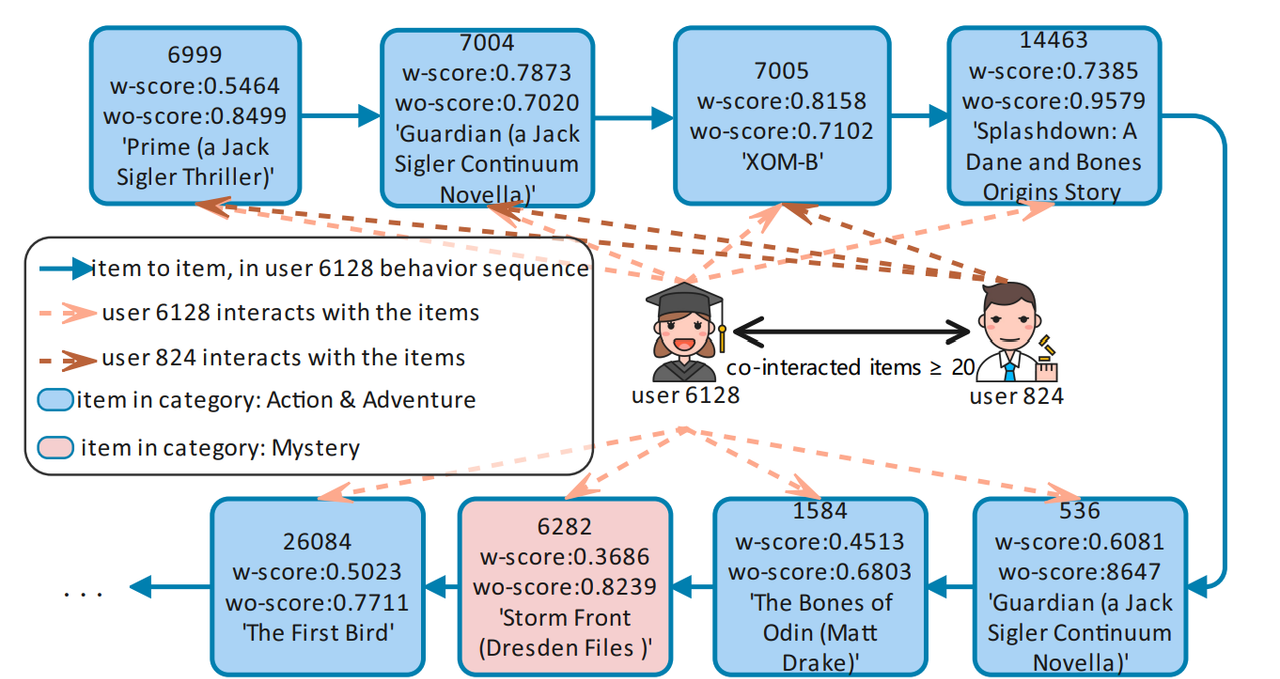
Figure 5: user-item scores for user $u_ a$ (6128) for specific behavior sequence with (w-score) and without (wo-score) self-augmented learning.
5. Conclusion
Liu et al (2024) propose a novel method to encode short and long-term user-item interactions for self-supervised learning by integrating the short-term embeddings into long-term ones. They further empirically show that their method outperforms state-of-the-art recommender system methods in top 10 and top 20 recommendations.
Importantly, they propose denoising short-term information for self-supervised learning by filtering it through long-term embeddings. This is intuitive, as we would expect long-term patterns to shape individual user preferences. Thus, short-term instances that deviate too much from the long-term patterns can safely be assumed to be noise.
A possible direction for future research could be making the time series continuous instead of discretized time intervals using methods like ordinary differential equations.
Author Information
- Author name: Christian Hvilshøj
- Affiliation: KAIST School of Computing
- Research Topic: Sequential Recommendation Learning
7. Reference & Additional materials
- Main paper: Liu, Yuxi, Lianghao Xia, and Chao Huang. “SelfGNN: Self-Supervised Graph Neural Networks for Sequential Recommendation.” Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2024.
- Github Implementation
- Reference
Vaswani, A. “Attention is all you need.” Advances in Neural Information Processing Systems (2017).
Yingqiang Ge, Shuya Zhao, Honglu Zhou, Changhua Pei, Fei Sun, Wenwu Ou, and Yongfeng Zhang. 2020. Understanding echo chambers in e-commerce recommender systems. In SIGIR. 2261–2270.
Wei Wei, Chao Huang, Lianghao Xia, and Chuxu Zhang. 2023. Multi-modal self-supervised learning for recommendation. In WWW. 790–800.
Jinghao Zhang, Yanqiao Zhu, Qiang Liu, Shu Wu, Shuhui Wang, and Liang Wang. 2021. Mining latent structures for multimedia recommendation. In MM. 3872–3880
Mengqi Zhang, Shu Wu, Xueli Yu, Qiang Liu, and Liang Wang. 2023. Dynamic Graph Neural Networks for Sequential Recommendation. IEEE Transactions on Knowledge and Data Engineering (TKDE) 35, 5 (2023), 4741–4753.
Jianxin Chang, Chen Gao, Yu Zheng, Yiqun Hui, Yanan Niu, Yang Song, Depeng Jin, and Yong Li. 2021. Sequential recommendation with graph neural networks. , 378–387 pages
Ruining He and Julian McAuley. 2016. Ups and Downs: Modeling the Visual Evolution of Fashion Trends with One-Class Collaborative Filtering. In WWW. 507–517
Eunjoon Cho, Seth A. Myers, and Jure Leskovec. 2011. Friendship and mobility: user movement in location-based social networks. In KDD. 1082–1090.
F. Maxwell Harper and Joseph A. Konstan. 2015. The MovieLens Datasets: History and Context. ACM Transactions on Interactive Intelligent Systems (TIIS) (2015).
Yehuda Koren, Robert Bell, and Chris Volinsky. 2009. Matrix Factorization Techniques for Recommender Systems. Computer 42, 8 (2009), 30–37.
Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. 2017. Neural Collaborative Filtering. In WWW. 173–182.
Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk.
- Session-based Recommendations with Recurrent Neural Networks. In ICLR
Wang-Cheng Kang and Julian McAuley. 2018. Self-Attentive Sequential Recommendation. In ICDM. IEEE, 197–206.
Jiacheng Li, Yujie Wang, and Julian McAuley. 2020. Time Interval Aware SelfAttention for Sequential Recommendation. In WSDM. 322–330.
Fei Sun, Jun Liu, Jian Wu, Changhua Pei, Xiao Lin, Wenwu Ou, and Peng Jiang.
- BERT4Rec: Sequential Recommendation with Bidirectional Encoder Representations from Transformer. In CIKM. 1441–1450.
Xiang Wang, Xiangnan He, Meng Wang, Fuli Feng, and Tat-Seng Chua. 2019. Neural graph collaborative filtering. In SIGIR. 165–174.
Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, YongDong Zhang, and Meng Wang. 2020. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In SIGIR.
Shu Wu, Yuyuan Tang, Yanqiao Zhu, Liang Wang, Xing Xie, and Tieniu Tan. 2019. Session-based recommendation with graph neural networks. In AAAI, Vol. 33. 346–353.
Ziyang Wang, Wei Wei, Gao Cong, Xiao-Li Li, Xian-Ling Mao, and Minghui Qiu. 2020. Global context enhanced graph neural networks for session-based recommendation. In SIGIR. 169–178
Yongjun Chen, Zhiwei Liu, Jia Li, Julian McAuley, and Caiming Xiong. 2022. Intent Contrastive Learning for Sequential Recommendation. In WWW. 2172–2182.
Xiaohan Li, Mengqi Zhang, Shu Wu, Zheng Liu, Liang Wang, and S Yu Philip.
- Dynamic Graph Collaborative Filtering. In ICDM. IEEE, 322–331.
Ziwei Fan, Zhiwei Liu, Jiawei Zhang, Yun Xiong, Lei Zheng, and Philip S. Yu.
- Continuous-Time Sequential Recommendation with Temporal Graph Collaborative Transformer. In CIKM. 433–442
Jiancan Wu, Xiang Wang, Fuli Feng, Xiangnan He, Liang Chen, Jianxun Lian, and Xing Xie. 2021. Self-supervised graph learning for recommendation. In SIGIR. 726–735.
Zhiwei Liu, Yongjun Chen, Jia Li, Philip S Yu, Julian McAuley, and Caiming Xiong. 2021. Contrastive Self-supervised Sequential Recommendation with Robust Augmentation
Xin Xia, Hongzhi Yin, Junliang Yu, Yingxia Shao, and Lizhen Cui. 2021. SelfSupervised Graph Co-Training for Session-based Recommendation. In CIKM. 2180–2190.
Yu Zheng, Chen Gao, Jianxin Chang, Yanan Niu, Yang Song, Depeng Jin, and Yong Li. 2022. Disentangling Long and Short-Term Interests for Recommendation. In WWW. 2256–2267.
Yuhao Yang, Chao Huang, Lianghao Xia, Yuxuan Liang, Yanwei Yu, and Chenliang Li. 2022. Multi-Behavior Hypergraph-Enhanced Transformer for Sequential Recommendation. In KDD. 2263–2274.
Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks.” arXiv preprint arXiv:1609.02907 (2016).
Cho, Kyunghyun. “Learning phrase representations using RNN encoder-decoder for statistical machine translation.” arXiv preprint arXiv:1406.1078 (2014).
Xia, Lianghao, et al. “Automated self-supervised learning for recommendation.” Proceedings of the ACM Web Conference 2023. 2023.