[NeurIPS-24] SPA: A Graph Spectral Alignment Perspective for Domain Adaptation
Overview
This paper introduces SPA (graph SPectral Alignment perspective), an innovative method for Unsupervised Domain Adaptation (UDA) that leverages graph spectral alignment. UDA addresses the challenge of adapting a model trained on a labeled source domain to perform well on an unlabeled target domain with different data distributions. Traditional UDA methods mainly focus on aligning features between domains and often overlook the rich intra-domain structures within each domain, therefore reducing the model’s ability to discriminate between classes. SPA offers a hierarchical framework that combines coarse graph alignment using spectral regularization with fine-grained message propagation through a neighbor-aware self-training mechanism. By doing so, SPA effectively balances the transfer of features across domains while maintaining discriminability within the target domain.
1. Introduction
The main challenge in UDA is to predict labels for the target domain data without access to labeled target data during training. Existing UDA methods primarily emphasize inter-domain transferability by aligning source and target domains to reduce domain shift. However, the authors claim that there exists trade of between learning a representation that is domain invariant, and learning a representation that results in maximum separabaility of the target domain.
The key innovation of this paper is the introduction of a graph spectral alignment perspective, which allows for an intrinsic and flexible alignment of the source and target domains without the need for restrictive point-wise matching. By casting the UDA problem into graph primitives, the authors aim to capture both inter-domain and intra-domain relations. The alignment of two domains via SPA appears to be more flexible and as a result the neighbor-aware self-training mechanism is able to further refines the target domain representations, improving discriminability.
2. Problem Definition
Formally, given:
-
Source Domain Data: $D_ s = { (x_ i^s, y_ i^s) }_ {i=1}^{N_ s}$, where $x_ i^s$ are the samples and $y_ i^s$ are the labels associated with the given samples, $N_ s$ is the number of labeled samples associated with $C_ s$ categorites.
-
Target Domain Data: $D_ t = { x_ i^t }_ {i=1}^{N_ t}$, where $x_ i^t$ are $N_ t$ unlabeled samples associated with $C_ t$ labels.
The goal of UDA is to learn a model that accurately predicts the labels ${y_ i^t}_ {i=1}^{N_ t}$ for the target domain samples $x_ i^t$. Both domains are assumed to share the same feature space and label space but to have different marginal data distributions.
3. Related Works
3.1 Adversarial Methods
Adversarial methods, such as Domain-Adversarial Neural Networks (DANN)[1], aim to learn domain-invariant features by confusing a domain classifier in an adversarial setup. While effective in reducing domain discrepancies, these methods often neglect intra-domain structures, which can reduce the model’s ability to discriminate between classes within the target domain.
3.2 Discrepancy-Based Methods
Discrepancy-based approaches, like Correlation Alignment (CORAL)[2], focus on minimizing statistical differences between source and target feature distributions. They primarily emphasize inter-domain transferability but often overlook the intra-domain relationships essential for maintaining class discriminability in the target domain.
3.3 Graph-Based Methods
Graph-based UDA methods capture relationships between samples by constructing and aligning graphs based on structural properties. Techniques like Bipartite Spectral Matching (BSP)[3] align domain graphs to enhance transferability. However, these methods rely on explicit, point-wise graph matching, which can be restrictive and computationally intensive, and insufficiently address intra-domain discriminability.
3.4 Novelty of SPA
The proposed SPA (Spectral Alignment Perspective) advances UDA by effectively balancing inter-domain transferability and intra-domain discriminability through a hierarchical framework:
-
Graph Spectral Alignment: SPA introduces a spectral regularizer that aligns source and target domain graphs in the eigenspace by minimizing the spectral distance between their Laplacian eigenvalues. This implicit alignment captures essential topological features without restrictive point-wise matching.
-
Neighbor-aware Self-training: SPA incorporates a neighbor-aware propagation mechanism that enhances discriminability within the target domain. By generating pseudo-labels using a weighted K-Nearest Neighbors (kNN) algorithm, it encourages smoothness among neighboring predictions and maintains class distinctions.
-
Joint Balancing Mechanism: By integrating spectral alignment with neighbor-aware propagation, SPA ensures domain alignment reduces transfer gaps while preserving and enhancing intra-domain structures for high discriminability.
4. Methodology
4.1 Adversarial Domain Adaptation Framework
SPA contains an adversarial domain adaptation framework, which includes a feature encoder $F(\cdot)$, a classifier $C(\cdot)$, and a domain classifier $D(\cdot)$. The feature encoder extracts features from input data, the classifier predicts class labels based on these features, and the domain classifier distinguishes between source and target domain features.
There are four objective functions parallely optimized. The supervised loss and adversarial loss components are defined as follows. The supervised loss component trains the model to learn the label information and the adversarial loss helps regularize this information to be domain invariant.
-
Supervised Classification Loss: $L_ {\text{cls}} = \mathbb{E}_ {(x_ i^s, y_ i^s) \sim D_ s} \left[ L_ {\text{ce}} \left( C(F(x_ i^s)), y_ i^s \right) \right]$, where $L_ {\text{ce}}$ is the cross-entropy loss.
-
Adversarial Loss: $L_ {\text{adv}} = \mathbb{E}_ {x_ i^s \sim D_ s} \left[ \log D(F(x_ i^s)) \right] + \mathbb{E}_ {x_ i^t \sim D_ t} \left[ \log \left( 1 - D(F(x_ i^t)) \right) \right]$
4.2 Dynamic Graph Construction
In order to model relationships between different samples within a give domain, SPA constructs self-correlation graphs for both the source and target domains. The nodes in the graph represent the feature embeddings of the samples from the feature encoder. The edges are weighted similarity between the node features, based on a similarity function such as cosine similarity. The graphs are dynamic in nature as they evolve as the feature encoder updates during training.
-
Nodes: Each node represents a sample’s feature embedding from the feature encoder:
-
Source nodes: $f_ i^s = F(x_ i^s)$
-
Target nodes: $f_ i^t = F(x_ i^t)$
-
-
Edges: Edges are weighted based on a similarity function $\delta(f_ i, f_ j)$, such as cosine similarity.
-
Dynamic Nature: The graphs are dynamic because $f_ i^s$ and $f_ i^t$ evolve as the feature encoder $F$ updates during training.
4.3 Graph Spectral Alignment
Based on the constructed correlation graphs, the domain alignment could be phrased as a graph alignment problem. The graph spectral alignment is achieved by minimizing the spectral distance between the Laplacian eigenvalues of the source and target domain graphs. This implicit alignment avoids the need for explicit, restrictive point-wise matching.
SPA introduces a spectral regularizer to align the source and target graphs:
-
Compute the graph Laplacian $L$ for each graph.
-
Obtain the eigenvalues $\Lambda$ of the Laplacian matrices for both source ($\Lambda^s$) and target ($\Lambda^t$) graphs.
-
Define the Spectral Distance: $L_ {\text{gsa}} = \left\vert \Lambda^s - \Lambda^t \right\vert_ p$ ,where $\left\vert \cdot \right\vert_ p$ denotes the $L_ p$ norm.
- Objective: Minimize $L_ {\text{gsa}}$ to encourage the source and target graphs to have similar spectral properties, aligning them in the eigenspace.
4.4 Neighbor-aware Propagation Mechanism
After the spectral alignment, rich topological information is transfered to the target domain. In order to enhance discriminability within the target domain, SPA introduces a neighbor-aware self-training mechanism. This mechanism generates pseudo-labels for each target sample based on the top k nearest labelled samples using K-Nearest Neighbor (KNN) algorithm.
-
Pseudo-label Generation: Let $p_ i = C(F(x_ i))$ denote prediction probabilities for target samples $x_ i^t$, and $p _i^m$ denote the mapped probability stored in the memory bank.
-
Voting Mechanism: Each target sample $x_ i^t$ considers its $k$ nearest neighbors $N_ i$. The neighbors of the node vote for the class labels, weighted by their predicted probabilities.
-
Compute the weighted vote for class $c$ as $q_ {i,c} = \sum_ {j \in N_ i} p_ {j,c}^m$ and normalize to get the confidence $\hat{q}_ {i,c}$, which is computed as $\hat{q}_ {i,c} = \frac{q_ {i,c}}{\sum_ {m=1}^{C_ t} q_ {i,m}}$
-
Assign the pseudo-label: $\hat{y}_ i = \arg\max_ c \hat{q}_ {i,c}$
-
-
Memory Bank: The Memory Bank plays a vital role in the neighbor-aware propagation mechanism by storing sharpened predictions and normalized features for target samples. Sharpening is achieved through the equation:
-
Sharpening reduces prediction ambiguity: $\tilde{p}_ {j,c} = \frac{p_ {j,c}^{1/\tau}}{\sum_ {x=1}^{C_ t} p_ {j,x}^{1/\tau}}$, where $\tau$ is the temperature parameter.
-
Exponential Moving Average (EMA) updates the stored predictions and features over iterations.
-
-
Neighbor-aware Propagation Loss: $L_ {\text{nap}} = -\alpha \cdot \frac{1}{N_ t} \sum_ {i=1}^{N_ t} \hat{q}_ {i, \hat{y}_ i} \log p_ {i, \hat{y}_ i}$
- $\alpha$ is a scaling coefficient that increases over iterations.
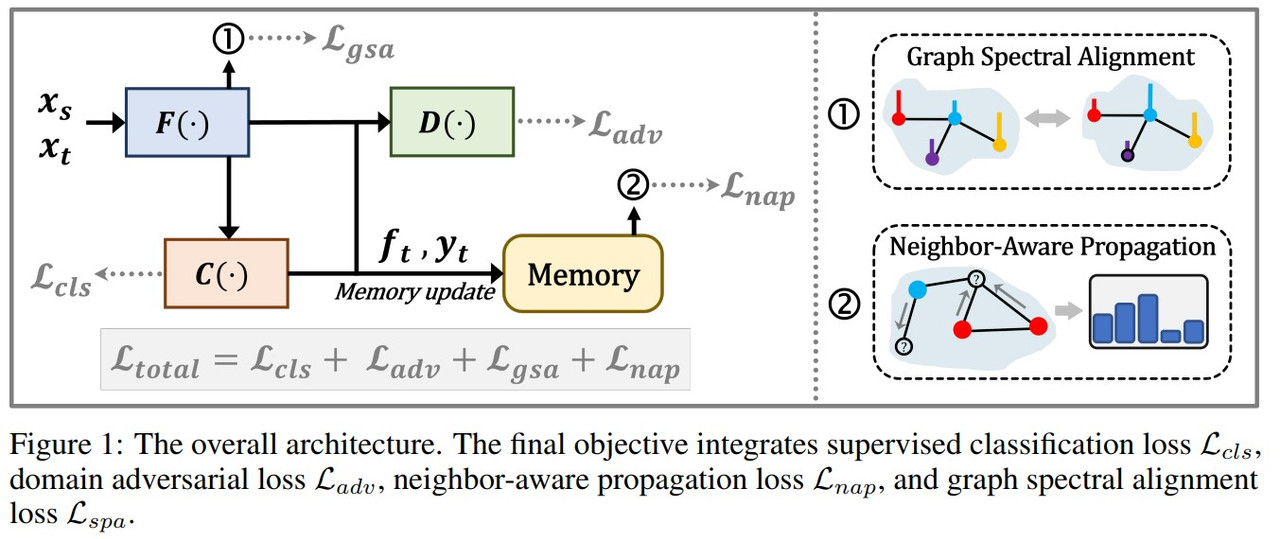
4.5 Final Objective
The overall loss function combines all components:
$L_ {\text{total}} = L_ {\text{cls}} + \lambda_ {\text{adv}} L_ {\text{adv}} + \lambda_ {\text{gsa}} L_ {\text{gsa}} + \lambda_ {\text{nap}} L_ {\text{nap}}$
This objective aims to:
-
Learn discriminative features on the source domain ($L_ {\text{cls}}$).
-
Align the source and target domains ($L_ {\text{adv}}$ and $L_ {\text{gsa}}$).
-
Refine target domain representations through neighbor-aware propagation ($L_ {\text{nap}}$).
5. Experiments
5.1 Experimental Setup
-
Datasets:
-
Office31: 4,652 images, 31 categories, 3 domains (Amazon, DSLR, Webcam).
-
OfficeHome: ~15,500 images, 65 categories, 4 domains (Artistic, Clipart, Product, Real-World).
-
VisDA2017: Over 280,000 images, 12 categories, synthetic-to-real domain adaptation.
-
DomainNet: ~600,000 images, 345 categories, 6 domains (Clipart, Infograph, Painting, Quickdraw, Real, Sketch).
-
-
Baselines: Compared with state-of-the-art UDA methods like DANN, CDAN, MDD, and others.
-
Backbone Networks:
-
ResNet-50 for Office31 and OfficeHome.
-
ResNet-101 for VisDA2017 and DomainNet.
-
-
Optimization:
-
Optimizer: Stochastic Gradient Descent (SGD) with momentum.
-
Learning Rate: Initialized at 0.01 with specific schedules.
-
Weight Decay: Set to 0.005.
-
5.2 Results
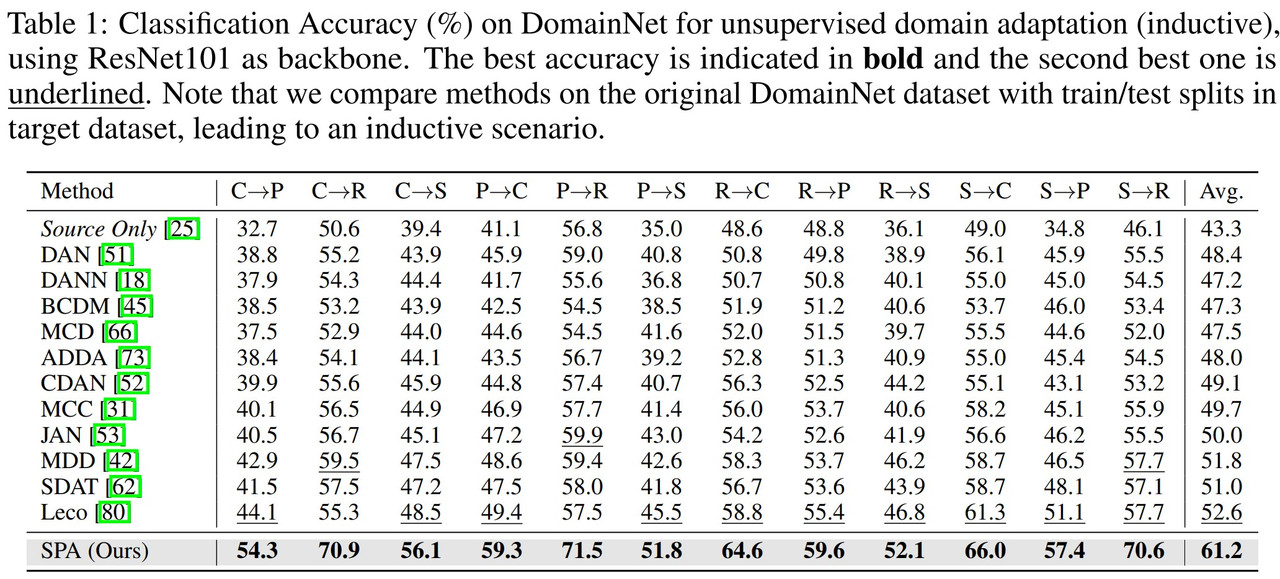
In the DomainNet dataset, Table 1, SPA achieved an 8.6% improvement in accuracy over previous state-of-the-art methods, demonstrating superior performance in handling large-scale datasets with significant domain gaps.
On the OfficeHome dataset, SPA showed approximately a 2.6% improvement in accuracy over existing methods, consistently outperforming competitors in all 12 adaptation scenarios. The results are presented in Table 2.

For the Office31 and VisDA2017 datasets, SPA performed on par with or better than state-of-the-art methods, showcasing its robustness and effectiveness across all domain pairs and tasks. In terms of evaluation metrics, classification accuracy on target domains was used, and SPA consistently showed improvements when compared to methods like DANN, CDAN, and MDD across all datasets. Refer to Table 3 for detailed results.

The authors also conduct t-SNE visualization to show the learning ability of SPA. They present the embeddings of source and target domain performed by SPA and three Baseline models DANN[1], BSP[3], and NPL[4] in figure 2. The authors claim that (i) embedding clusters by SPA are more compact, signifying the better discriminability achieved, and (ii) the source and target domain embeddings are more aligned in SPA, the red markers are closer to the blue markers, indicating better transferability. However, the authors do not present any quantitative evidence to support these claims, leaving their conclusions open to question.

6. Discussion and Conclusion
6.1 Efficacy and Robustness
- SPA effectively balances inter-domain transferability and intra-domain discriminability, making it an efficient method. Its robustness is demonstrated across different datasets and domain shifts, showing that it can adapt well to various scenarios without a significant drop in performance.
6.2 Comparison with Related Works
- SPA distinguishes itself from methods like BSP and SIGMA by using implicit graph alignment through spectral regularization. This approach avoids the limitations of point-wise matching that are present in other techniques. Additionally, SPA’s neighbor-aware propagation mechanism enhances discriminability within the target domain, countering potential reductions that could arise from external regularization.
6.4 Conclusion
- SPA introduces a novel approach to unsupervised domain adaptation by integrating graph spectral alignment with a neighbor-aware propagation mechanism. It effectively addresses the limitations of existing methods by considering both inter-domain and intra-domain relations. The experiments show that SPA outperforms current state-of-the-art methods, significantly improving accuracy while maintaining a balance between transferability and discriminability.
7. Author Information
- Zhiqing Xiao
- College of Computer Science and Technology, Zhejiang University
- Key Lab of Intelligent Computing based Big Data of Zhejiang Province, Zhejiang University
8. References and Additional Materials
Xiao, Z., Wang, H., Jin, Y., Feng, L., Chen, G., Huang, F., & Zhao, J. (2023). SPA: A Graph Spectral Alignment Perspective for Domain Adaptation. arXiv preprint arXiv:2310.17594.
-
GitHub Repository: https://github.com/CrownX/SPA
-
Paper Reference:
-
[1] Yaroslav Ganin and Victor Lempitsky. Unsupervised domain adaptation by back propagation. In Proceedings of the 32th International Conference on Machine Learning (ICML), pages 1180–1189. PMLR, 2015.
- [2] Baochen Sun and Kate Saenko. Deep coral: Correlation alignment for deep domain adaptation. In ECCV 2016 Workshops, 2016.
- [3] Xinyang Chen, Sinan Wang, Mingsheng Long, and Jianmin Wang. Transferability vs. discriminability: Batch spectral penalization for adversarial domain adaptation. In Proceedings of the 36th International Conference on Machine Learning (ICML), pages 1081–1090. PMLR, 2019.
- [4] Lee, Dong-Hyun. “Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks.” Workshop on challenges in representation learning, ICML. Vol. 3. No. 2. 2013.
-