[WWW-2024] On the Feasibility of Simple Transformer for Dynamic Graph Modeling
===
세줄 요약
- 기존 Message passing GNNs(GAT, GCN)들은 모델 구조가 복잡해질수록 Over-smoothing, Over-squashing의 문제가 존재한다.
- 최근 Transformer 기반 모델들이 Static graph (t = T) 에 대해서 이 문제들을 잘 해결하고, 좋은 성능을 나타내고 있다.
- 본 논문은 Static graph에 적용되는 Transformer 기반 모델을 발전시켜 Dynamic graph (t = 1 ~ T) 에 적용하였다.
Introduction
기존 Message Passing GNN의 단점
GNN의 장점은 특정 node에 대해 이웃 node들이 미치는 네트워크 효과를 잘 포착한다는 점이다. 이를 위해 Graph Convolution Network(GCN), Graph Attention Network(GAT)와 같은 모델을 통해 주변 node에서 정보를 추출하는 방법론이 제시되었고, 최근까지 좋은 성능을 보여주었다. 하지만 해당 방법들은 주변 Node에서 정보를 추출하는 과정에서 GNN의 Layer가 증가하여 각 Node의 Embedding이 동일해지는 현상(Over-Smoothing)과 먼 Node에서 정보를 가져오는 과정에서 해당 정보가 손실되는 현상(Over-Squashing)의 단점이 관찰되었다.

Temporality with Transformer
기존 GNN 방법론들에서 Dynamic Graph의 temporality를 다루는 방법에는 크게 두 가지가 있다. Discrete time step GNN은 시간/일/월 등 특정한 시간 단위로 Snapshot을 찍은 후(ex: 1월 snapshot, 2월 snapshot, …) 그에 맞게 Graph를 나누어 다루는 방법이고, Continuous time step GNN은 말 그대로 연속적인 Graph의 변화를 보는 방법이다.
Discrete의 경우에는 Graph가 특정 시간대로 나뉘어 데이터를 다루기가 쉽다는 장점이 있지만, 해당 시간대 이하에서 나타나는 fine-grained temporality를 포착하기 어렵다는 단점이 있다. Continuous는 세부적인 temporality를 잃지 않는 장점이 있지만, 모델이 더 복잡해지고 Gradient vanishing 문제가 발생하여 Graph의 Long-term dependency를 잘 포착하지 못한다고 알려져있다.
Transformer를 사용하면 1. continous의 장점인 fine-grained temporality를 놓치지 않을 수 있고, 2. self-attention을 통해 long-term dependency의 성능이 향상된다. 3. Message passing GNNs의 단점인 Over-smoothing과 Over-squashing의 문제도 덜하다는 장점이 있다.
Related Works
Dynamic Graph Learning
Dynamic graph를 다루기 위해 제시된 주요 방법론은 다음과 같다.
- DySAT (WSDM 2020): GAT, Self-attention
- EvolveGCN (AAAI 2020): GCN, RNN
- TGAT (ICLR 2020): Temporal graph attention
- TGN (ICML 2020): Temporal graph attention
- GraphMixer (ICLR 2022): Temporal graph attention(MLP mixer)
Transfomer 기반 GNNs
최근에는 Transformer 구조를 사용해 Graph 구조를 파악하게 하는 연구들이 활발하게 진행되었는데, 대표적으로는 NeurIPS 2022에 발표된 Pure Transformers are Powerful Graph Learners가 있다. 이 논문에서는, vanila Transformer 구조에 Node, Edge와 같은 그래프 구성물들을 Node, Edge라고 표시해주는 Type identifier들만 추가하여 input으로 넣었을 때, 기존 Message Passing GNN에 기반한 SOTA 모델보다 좋은 성능을 냈다고 보고하고 있다.

Proposed Approach
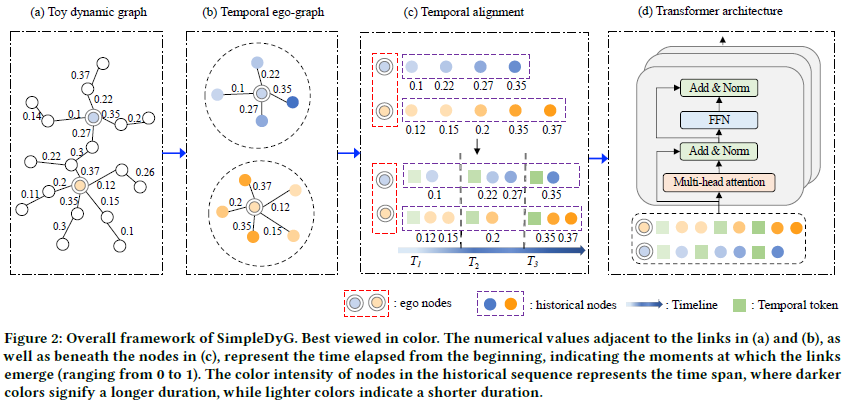
Temporal Ego-graph
Dynamic graph의 특성상 Static graph를 다뤘던 이전 논문 (Pure Transformers are Powerful Graph Learners)처럼 바로 Transformer에 Graph를 input으로 넣을 수 없기에, Temporal Ego-graph라는 subgraph을 Node마다 생성한다. Temporal Ego-graph는 Node $v$ 가 다른 Node들과 상호작용한 기록이 담겨있는 Graph로, 수식으로 표시하면 아래와 같다.
 $v^k_i$는 Node $v$가 Node $k$와 timestep $\tau$에 상호작용한 정보를 담고 있다($v_i, v_k, \tau$). training data $x_i$는 Node $i$에 대해 sequence length $w$만큼의 길이를 가지는 Temporal Ego-graph로, training data임을 Transformer model에 알려주기 위해 앞뒤로 $<\vert hist \vert >$와 $<\vert endofhist \vert >$ token으로 감싸주었다. $y_i$는 Node i의 label data로, 상세 사항은 $x_i$와 같다.
$v^k_i$는 Node $v$가 Node $k$와 timestep $\tau$에 상호작용한 정보를 담고 있다($v_i, v_k, \tau$). training data $x_i$는 Node $i$에 대해 sequence length $w$만큼의 길이를 가지는 Temporal Ego-graph로, training data임을 Transformer model에 알려주기 위해 앞뒤로 $<\vert hist \vert >$와 $<\vert endofhist \vert >$ token으로 감싸주었다. $y_i$는 Node i의 label data로, 상세 사항은 $x_i$와 같다.
Temporal Alignment
Transformer model이 자연적으로 sequence의 상대적 위치에 따라 temporality를 학습하기는 하지만, 서로 다른 Node 간에는 다른 time step을 따르는 맹점이 아직 남아있다. 다음과 같은 예시를 보자
- Node $u$는 24년 1월에 Graph에 추가되어 sequence가 $w_u$ = <$v_u^{24년 1월}$,$v_u^{24년 2월}$, …, $v_u^{24년 10월}$>이고,
- Node $k$는 23년 7월에 Graph에 추가되어 sequence가 $w_k$ = <$v_k^{23년 7월}$,$v_k^{23년 8월}$, …, $v_k^{24년 10월}$>이라면 Transformer model은 해당 sequence들만으로는 $v_u^{24년 1월}$와 $v_k^{23년 7월}$가 같은 time step에 일어났는지 판단할 수 없다. 이에 저자들은 특정 time step마다 다른 Temporal token을 삽입하여, Node전체에 적용되는 universal timeline을 부여하고자 하였다.
Training objectives
Joint Probability 정의
생성한 Temporal Ego-graph에 Temporal Alignment과정을 통해 Temporal token을 추가한 sequence를 $R = <r_1, r_2, …, r_{\vert R \vert }>$이라고 하자($\vert R \vert $은 Sequence R의 길이). 해당 sequence의 joint probability는 아래와 같이 표현할 수 있다.
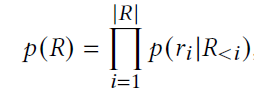
Conditional Probability and Loss
$p(r_i \vert R_{<i})$는 $R_{<i}$까지의 token이 주어졌을 때 step i에서의 token의 probability distribution이다. 이 때 중요한 것은 i번째 token을 예측할 때 미래참조편향을 방지하기 위해 i 혹은 i보다 뒤에 오는 token들은 masking을 한 채로 probability distribution을 생성해야한다는 것이다. 그 결과 아래 식과 같이 놓고 train할 수 있다. $R^l_<i$는 i번째 token 전까지 generated 된 token들의 transformer 속 hidden layer이고, 여기에 learnable matrix인 $W_{vocab}$을 곱해준다.
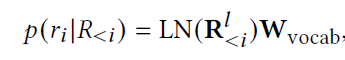 결과적으로 이를 Negative log-likelihood 방식으로 바꾸면 아래와 같이 loss를 정의할 수 있다.
결과적으로 이를 Negative log-likelihood 방식으로 바꾸면 아래와 같이 loss를 정의할 수 있다.
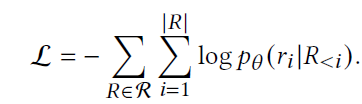
Overall Algorithm
위와 같이 정의한 Probability distribution을 활용한 Training algorithm은 다음과 같다.
- Traning sample에서 batch를 고른다.
- i 직전까지의 generated token을 Masked Transformer를 통과시켜 $R_<i$를 얻는다.
- 위에 보인 식들을 활용해 joint probability를 얻는다.
- loss를 구하고 반복한다.

Experiments
Datasets
- UCI: SNS 상에서 user들간의 message 교환 기록이 있는 dataset
- ML-10M: MovieLens dataset 중 하나로, user들이 각 영화들에 대해 어떤 tag를 부여했는지가 나와있는 dataset
- Hepth: 고에너지 물리학 논문들의 citation network
- MMConv: Multi-turn task oriented dialogue dataset
Evaluation Metrics
저자들은 위의 Dataset을 기반으로, given time step에 link prediction task를 진행하였다. 모델이 제시한 예상 node 결과와 ground truth의 ranking performance, similarity를 분석하기 위해 아래와 같은 두 가지 evaluation metric을 사용하였다.
- NDCG@5: 추천시스템/검색 엔진 평가에 자주 쓰이는 Metric으로, Top 5개의 추천 항목을 기준으로 함
- Jaccard Similarity: 추천 set과 정답 set의 유사도를 측정하는 지표
Results
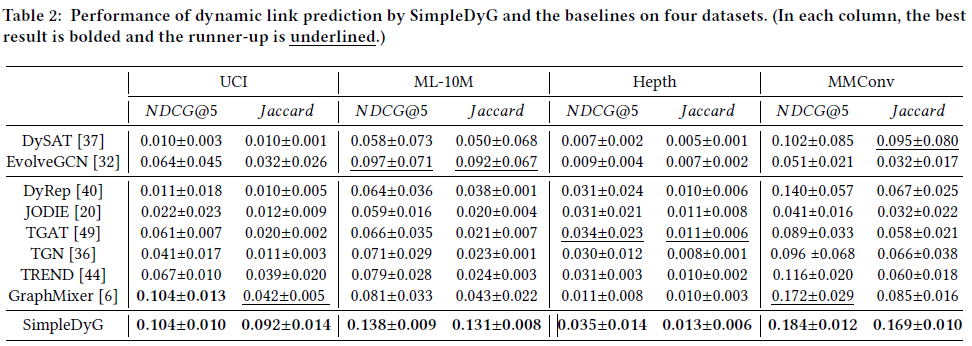 왼쪽이 baseline과 simpleDyG 등 모델, 위쪽이 Dataset의 종류이다.
4개 dataset 모두에서 NDCG@5와 Jaccard 모두 해당 논문의 방법론인 SimpleDyG가 최고 성능을 보였다.
왼쪽이 baseline과 simpleDyG 등 모델, 위쪽이 Dataset의 종류이다.
4개 dataset 모두에서 NDCG@5와 Jaccard 모두 해당 논문의 방법론인 SimpleDyG가 최고 성능을 보였다.
Effect of Extra Tokens
Impact of Special Tokens

Special tokens(“<$\vert$ hist $\vert$ >”, “<$\vert$ endofhist $\vert$ >”, “<$\vert$ pred $\vert$ >”, “<$\vert$ endofpred $\vert$ >”)와 같은 special token의 효과를 알아보기 위해 두 가지 Ablation 실험을 진행하였다.
- SimpleDyG: 원 모델, 각기 다른 special token 사용(ex: hist, endofhist, pred, endofpred)
- same special: 같은 special token 사용(ex: x, x, x, x)
- no special: special token 미사용 결과적으로는 dataset에 따라 SimpleDyG와 same special이 엎치락뒤치락하는 모습을 보여주었다. 특이하게도 Hepth dataset에서는 no special 모델이 가장 좋은 성능을 보였는데, 이는 scientific paper citation network인 Hepth dataset의 특징 때문이라고 생각된다. Test set의 ego-node가 새로운 node(newly published paper)여서, historical information이 큰 영향을 미치지 못했다고 해석할 수 있다.
Impact of Temporal Tokens
 Temporal tokens의 효과를 알아보기 위해 역시 두 가지 Ablation 실험을 진행하였다.
Temporal tokens의 효과를 알아보기 위해 역시 두 가지 Ablation 실험을 진행하였다.
- SimpleDyG: 원 모델, 각기 다른 temporal token 사용(ex: 24년 1월, 24년 2월, …)
- same time: 같은 temporal token 사용(ex: x, x, …)
- no time: temporal token 미사용 결과를 보면, 의외로 same time이나 no time의 결과가 좋은데, 이는 transformer 모델에게 temporality를 자연스럽게 배우게 하는 것이 인위적인 temporal token을 부여하는 것보다 때때로 더 나을 수 있다고 해석할 수 있다.
Performance of Multi-step Prediction
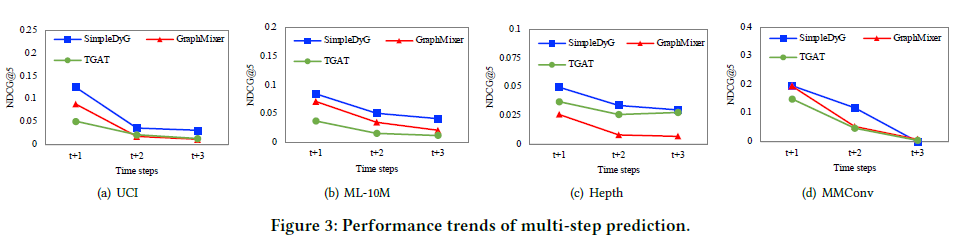 t시점에서 단순히 다음 time step인 t+1만 예측하는 것이 아닌, 그 이후를 예측하는 성능을 검증하기 위해 다른 baseline 모델과 비교 실험을 해본 결과이다. 당연하지만 t+3으로 갈수록 모델의 성능이 낮아지지만, SimpleDyG가 다른 baseline model인 TGAT과 GraphMixer보다 꾸준히 성능이 낫다는 것을 보여준다.
t시점에서 단순히 다음 time step인 t+1만 예측하는 것이 아닌, 그 이후를 예측하는 성능을 검증하기 위해 다른 baseline 모델과 비교 실험을 해본 결과이다. 당연하지만 t+3으로 갈수록 모델의 성능이 낮아지지만, SimpleDyG가 다른 baseline model인 TGAT과 GraphMixer보다 꾸준히 성능이 낫다는 것을 보여준다.
Hyper-parameter Analysis
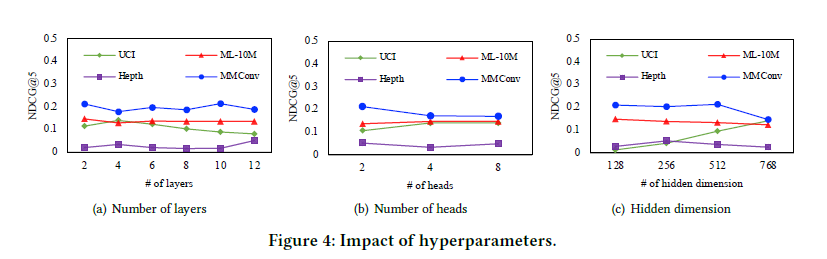 Hyper-parameter에 따른 성능 변화도 꽤나 robust한 결과를 보여주어, 특정한 setting에서만 성능이 좋은 것이 아니라는 것을 입증한다.
Hyper-parameter에 따른 성능 변화도 꽤나 robust한 결과를 보여주어, 특정한 setting에서만 성능이 좋은 것이 아니라는 것을 입증한다.
Conclusion
본 논문은 그래프 분석에 Transformer를 도입하려는 최근의 연구흐름 속에서 Dynamic graph에의 적용을 다룬 논문이다. Dynamic graph의 특징인 Temporality를 도입하기 위해 저자들은 새로운 방법인 Temporal ego-graph과 Temporal alignment를 도입하였고, 4가지 dataset에서 기존 baseline model들보다 성능이 좋다는 것을 여러 실험으로 밝혔다.
저자들이 제안한 방법론은 vanila Transformer 구조를 사용해 구현이 쉽다는 장점이 있고, 추가적인 Transformer 구조의 수정 없이도 SOTA 성능을 보이는 것을 보여주어 Dynamic graph에서의 Transformer 적용가능성을 열었다.
하지만, Temporal ego-graph 구조가 다른 graph dataset에서도 알맞은 구조인지와 Ablation에서 보았듯이 Temporal alignment 구조가 꼭 필요한지에 대한 의문이 있다. 추가로 heterogeneous graph나 knowledge graph와 같은 복잡한 graph에서도 적용가능한지 후속연구가 필요하다.
Author Information
- Donggyu Lee
- Affiliation: Graduate School of Data Science, advised by Jihee Kim
- Research Topic: NLP, GIS, Economics, Finance
Reference & Additional materials
- Arxiv page: https://arxiv.org/abs/2401.14009
- Github repo: https://github.com/YuxiaWu/SimpleDyG
- OpenReview page of paper: https://openreview.net/forum?id=6nnkyxQayj&referrer=%5Bthe%20profile%20of%20Yuxia%20Wu%5D(%2Fprofile%3Fid%3D~Yuxia_Wu1)
- Author’s presentation: https://www.youtube.com/watch?v=7sS0yVRS_jM