[AAAI-24] No prejudice! Fair Federated Graph Neural Networks for Personalized Recommendation
1. Problem Definition
The primary issue addressed by this paper is the challenge of achieving fairness across demographic groups in Federated Learning (FL)-based recommendation systems (RSs), particularly while ensuring user privacy. Traditional, centralized recommendation systems tend to produce biased recommendations that favor certain demographic groups (e.g., gender or age), while also violating user privacy by gathering sensitive data on central servers. FL addresses privacy by decentralizing data processing, but ensuring fairness without demographic information remains unresolved. The goal of this paper is to develop a recommendation system that mitigates demographic biases within FL environments using Graph Neural Networks (GNNs), while preserving the privacy of sensitive user information and maintaining high utility for recommendations.
2. Motivation
2.1 Limitations and ChallengesRecommendation systems are widely used in industries like e-commerce and healthcare, but key challenges persist:
-
Privacy and Security: Traditional RSs rely on centralized data collection, where sensitive user information is stored and processed, leading to privacy violations [2].
-
Fairness Concerns: FL allows for the decentralized training of models on local devices and transmitting the updated model back to the server, to preserve user privacy. However, FL fails to ensure fairness across demographic groups [1] when sensitive data like gender or race, is unavailable for analysis [3].
-
Amplified Bias: GNNs are effective at modeling user-item interactions in RSs but can inherit and exacerbate existing biases in the data, making fairness even harder to achieve in FL environments [4].
The authors introduce F2PGNN (Fair Federated Personalized Graph Neural Network), a novel framework that addresses these issues through three key pillars:
-
Fairness: F2PGNN ensures fairness in recommendations without requiring access to sensitive demographic information.
-
Privacy: By using Local Differential Privacy (LDP), the model maintains user privacy while sharing group-level statistics.
-
Personalization: The system captures both higher-order and explicit user-item interactions through a GNN model, improving recommendation accuracy while reducing bias.
3. Related Work
Extensive research exists on fairness in recommendation systems and FL, but combining fairness with privacy-preserving techniques in FL remains challenging. Previous studies on fairness in centralized recommendation systems, such as those by Yao and Huang (2017) [5] and Li et al. (2021) [6], focus on mitigating bias using demographic data. However, these methods require access to centralized data, which violates privacy norms.
In the federated learning domain, models like FedMF [7] and FedPerGNN [8] have integrated fairness into federated settings, but they either rely on Matrix Factorization, which lacks the ability to model higher-order interactions, or introduce significant computational overhead with encryption techniques.
This paper builds on existing works but proposes a more efficient and scalable solution by utilizing GNNs for recommendation and adding privacy constraints through LDP, ensuring fairness while preserving privacy.
4. Methodology
The proposed F2PGNN is designed to ensure fairness in federated recommendation systems by leveraging GNNs, which allow users to train models locally while preserving privacy. Below are the core components of this framework:
4.1 Inductive Graph Expansion AlgorithmOne of the key innovations in the F2PGNN framework is the Inductive Graph Expansion algorithm, which allows users to incorporate higher-order interactions into their local user-item interaction graphs. Higher-order interactions uncover latent relationships by connecting users who interacted with similar items, improving recommendation quality.
The steps in this algorithm are:
-
Users encrypt their item IDs using a public key.
-
These encrypted IDs are sent to a server, which matches them across different users to find co-interacted items (i.e., items that have been rated by multiple users).
-
The server provides anonymous embeddings for users who share interactions with the same items, allowing users to expand their graphs while maintaining privacy.
These expanded subgraphs allow clients to incorporate higher-order interactions, which significantly enhance recommendation quality.
4.2 Local GNN TrainingOnce users have expanded their local subgraphs, they train a Graph Attention Network (GAT) locally. GATs are particularly suited to recommendation systems as they allow the model to assign varying levels of importance to neighboring nodes (users or items), depending on the strength of their connections. GAT updates embeddings by aggregating information from neighbors, with attention mechanisms determining influence.
Mathematically, the attention coefficient between a user node $v$ and its neighbor $k$ is calculated as:
$e_ {vk} = \text{LeakyReLU}(\mathbf{a}^\top [\mathbf{W}\mathbf{h}_ v \vert \mathbf{W}\mathbf{h}_ k])$
Here, $h_ v$ and $h_ k$ are the feature vectors of nodes $v$ and $k$, respectively, and $\mathbf{W}$ is the weight matrix. The operator $\vert\vert$ denotes concatenation, and $\mathbf{a}$ is the attention weight vector that learns the relative importance of neighboring nodes. This attention score is then normalized across all neighbors $j \in \mathcal{N}_ v$ of node $v$:
$\alpha_ {vk} = \frac{\exp(e_ {vk})}{\sum_ {j \in N_v} \exp(e_ {vj})}$
The final node embedding $\mathbf{h}_ v’$ for node $v$ is updated by aggregating the normalized attention-weighted features from all its neighbors:
$\mathbf{h}’_ v = \sigma ( \sum_ {k \in N_ v} \alpha_ {vk} \mathbf{W}\mathbf{h}_ k )$
where $\sigma$ is a non-linear activation function (e.g., ReLU).
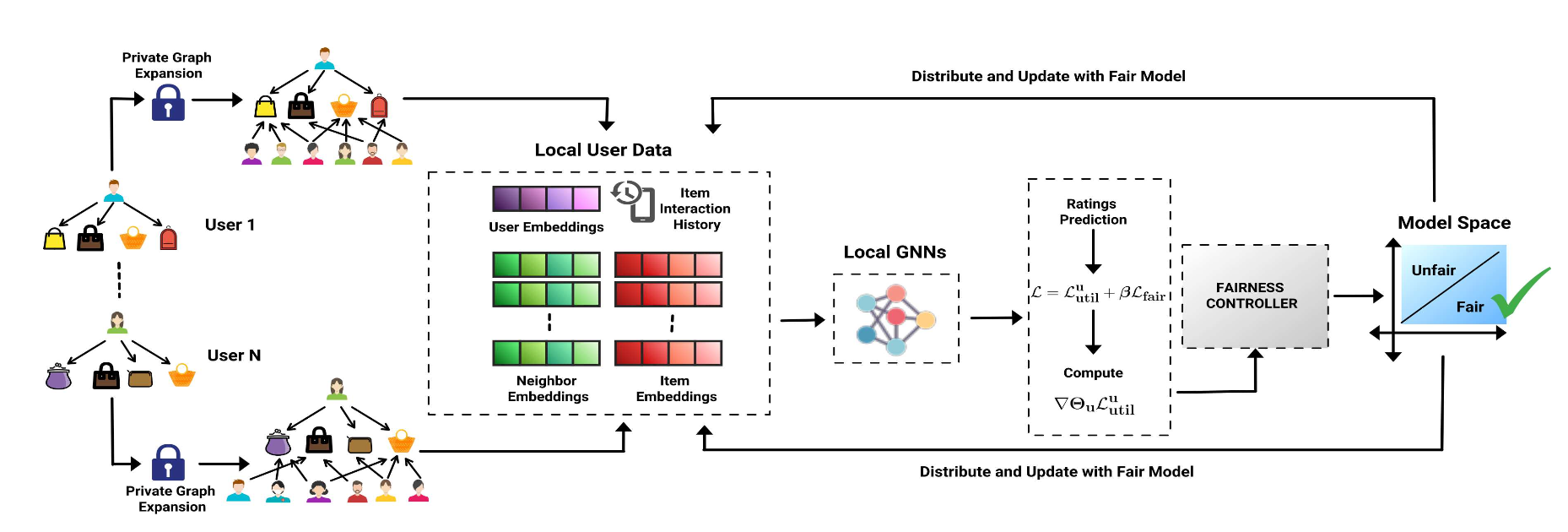
Figure 1: The overall structure of the F2PGNN framework.
4.3 Fairness-Aware Loss FunctionA core innovation of F2PGNN is its fairness-aware loss function, designed to ensure equitable recommendations across different demographic groups. The function balances utility (recommendation accuracy) and fairness (reducing demographic bias).
The overall loss function is defined as:
$L = L_{util} + \beta L_{fair}$
Here, $L_{util}$ is the utility loss, which can be the mean squared error (MSE) between the predicted and true ratings, and $L_{fair}$ is the fairness loss, which penalizes the model for disparities in performance across different demographic groups. The parameter $\beta$ controls the trade-off between utility and fairness, with higher values of $\beta$ placing more emphasis on fairness.
The fairness loss is defined as the absolute difference in the average performance of the model between two demographic groups $S_0$ (e.g., males) and $S_1$ (e.g., females):
$L_ {fair}(M, S_ 0. S_ 1) = \vert\frac{1}{S_ 0}\sum_ {u \in S_ 0}\mathcal{M}(u)-\frac{1}{S_ 0}\sum_ {u \in S_ 1}\mathcal{M}(u)\vert^\alpha$
where $\mathcal{M}(u)$ is the performance metric for user $u$ (e.g., the negative loss for user $u$) and $\alpha$ is an exponent that determines the severity of the fairness penalty (typically set to 1 or 2).
4.4 Fairness-Aware Gradient AdjustmentTo incorporate fairness into the training process, the gradients of the model are adjusted based on the fairness loss. This is crucial because it allows the model to reduce bias during training by controlling the learning speed for different groups.
Overperforming groups have reduced learning rates, while underperforming groups receive increased rates to promote fairness.
The adjusted gradient for user $u$ is computed using the following formula:
$\nabla \Theta_ u = (1 - \beta R\vert P - Q\vert^{\alpha-1}) \frac{\partial L^u_ \text{util}}{\partial \Theta_ u}$
where $\nabla \Theta_ u$ represents the gradient update for user $u$, $\beta$ is the fairness budget determining how much weight is given to fairness during training. $R$ is a scalar determined by the difference in performance between groups and user group membership:
$R = \alpha \cdot (-1)^{1(P<Q)} \cdot (-1)^{1(u \notin S_0)}$
$P$ and $Q$ represent the average performance metrics (e.g., accuracy or utility) for groups $S_0$ and $S_1$ respectively:
$P = \frac{1}{\vert S_ 0\vert} \sum_ {u \in S_ 0} \mathcal{M(u)}, \quad Q = \frac{1}{\vert S_ 1\vert} \sum_ {u \in S_ 1} \mathcal{M(u)}$
Here, $\mathcal{M(u)}$ represents the utility metric for user $u$, such as the recommendation accuracy.
The adjusted gradient ensures that:
-
Overperforming users (i.e., those in group $S_0$ if $P>Q$) experience slower learning, reducing potential biases toward their group.
-
Underperforming users (i.e., those in group $S_1$ if $P<Q$) experience faster learning, helping to close the performance gap.
Thus, fairness is promoted by adjusting the learning rates dynamically, ensuring that both groups are treated equitably during the training process.
4.5 Local Differential Privacy (LDP)To ensure privacy, F2PGNN employs LDP. This mechanism ensures that sensitive information (such as individual interactions or group membership) is obfuscated during model updates. LDP protects model gradients and group statistics used for fairness adjustments.
Model Updates: After computing the adjusted gradients, each user applies gradient clipping to ensure that the updates are bounded, followed by adding noise to the gradients using the Laplace mechanism. This results in differentially private gradient updates, which protect the user’s data even from inference attacks.
The clipped and noisy gradient is computed as follows:
$\nabla \Theta_u^\text{LDP} = \text{clip}(\nabla \Theta_u, \delta) + \text{Laplace}(0, \lambda)$
where $\text{clip}(\nabla \Theta_u, \delta)$ ensures that the gradient norm is bounded by $\delta$, and $\lambda$ controls the variance of the Laplace noise, with larger values of $\lambda$ providing stronger privacy but potentially reducing model accuracy.
Group Statistics Updates: To ensure fairness, the server needs to know the group-level statistics (i.e.,$P$ and $Q$) that measure the performance of different demographic groups. However, directly uploading these statistics could reveal sensitive group membership information. To address this, LDP is also applied to the group statistics updates.
For each user $u$ the server receives the following noisy updates:
$P_u^\text{perf} = \mathbb{I}(u \in S_0)\mathcal{M(u)} + \epsilon_1, \quad Q_u^\text{perf} = \mathbb{I}(u \in S_1)\mathcal{M(u)} + \epsilon_2$
$P_u^\text{count} = \mathbb{I}(u \in S_0) + \epsilon_3, \quad Q_u^\text{count} = \mathbb{I}(u \in S_1) + \epsilon_4$
where:
-
$\mathbb{I}(u \in S_0)$ is an indicator function that equals 1 if user $u$ belongs to group $S_0$ and 0 otherwise.
-
$\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4 \sim \mathcal{N}(0, \sigma^2)$ re noise terms drawn from a normal distribution with variance $\sigma^2$, ensuring privacy.
By adding noise to the group statistics, the server cannot accurately infer which users belong to each group, thus preserving privacy.
4.6 Training ProcessThe overall training process involves the following steps during each communication round:
-
Users receive the global model parameters and group statistics.
-
Each user expands their local graph using the Inductive Graph Expansion algorithm and trains their GNN on the expanded subgraph.
-
Users compute adjusted gradients that incorporate fairness scaling.
-
LDP is applied to both gradients and group statistics to preserve privacy.
-
Updated parameters and statistics are sent back to the server.
-
The server aggregates these updates, computes new global model parameters, and rebroadcasts them to the users.
Example:
In a movie recommendation system with two demographic groups (e.g., males and females), if the average recommendation accuracy for males is higher, the fairness-aware gradient adjustment will slow the learning rate for male users and increase it for female users to reduce group disparity.
5. Experiment
5.1 Experiment SetupThe experiments used three real-world datasets for recommendation tasks:
- MovieLens-100K (ML-100K): Contains 100,000 ratings from 943 users on 1,682 movies.
-
MovieLens-1M (ML-1M): A larger dataset with 1 million ratings from 6,040 users on 3,706 movies.
- Amazon-Movies: A large-scale dataset with approximately 500,000 ratings from 5,515 users on 13,509 movies.
In the experiments, two types of sensitive attributes were considered:
- Gender (G): Used to test gender bias mitigation.
- Activity Level (A): Evaluated fairness for users with different engagement levels.
The authors compare F2PGNN against the F2MF (Fair Federated Matrix Factorization) model, a federated recommendation system that also incorporates fairness constraints. However, F2MF does not utilize the graph structure of user-item interactions, which limits its ability to capture higher-order relationships. The comparison between these models aims to highlight the advantages of GNNs in federated learning environments, particularly in terms of balancing fairness and utility.
5.3 Evaluation MetricsTwo key metrics were used to evaluate the performance of the model:
-
Utility Metric: The accuracy of the recommendations was measured using Root Mean Square Error (RMSE). A lower RMSE indicates better prediction accuracy.
-
Fairness Metric: Fairness was measured using group unfairness, which calculates the absolute difference in average performance (RMSE) between demographic groups. Lower group unfairness scores indicate more equitable treatment of different user groups.
The experiments highlight the following findings:
- Fairness Improvement: F2PGNN significantly reduced group disparity across all datasets, with improvements up to 84% over the baseline (e.g., gender bias in MovieLens-1M).
- Utility Preservation: The model achieved competitive RMSE scores compared to F2MF, with only minor trade-offs under stronger fairness constraints.
- Fairness-Utility Trade-off: Customizable trade-offs were enabled through the fairness budget ($\beta$), making F2PGNN adaptable for fairness-critical applications like healthcare and e-commerce.
The table below summarizes F2PGNN’s performance and fairness compared to F2MF across datasets. _G denotes Gender, A denotes Activity.

Figure 2: Performance vs Fairness comparison with different fairness budget $\beta$.
Disparity vs. Epochs: Group disparity consistently decreased with F2PGNN, especially under higher $\beta$, as shown in the graph below. This highlights its effectiveness in reducing demographic bias over time.
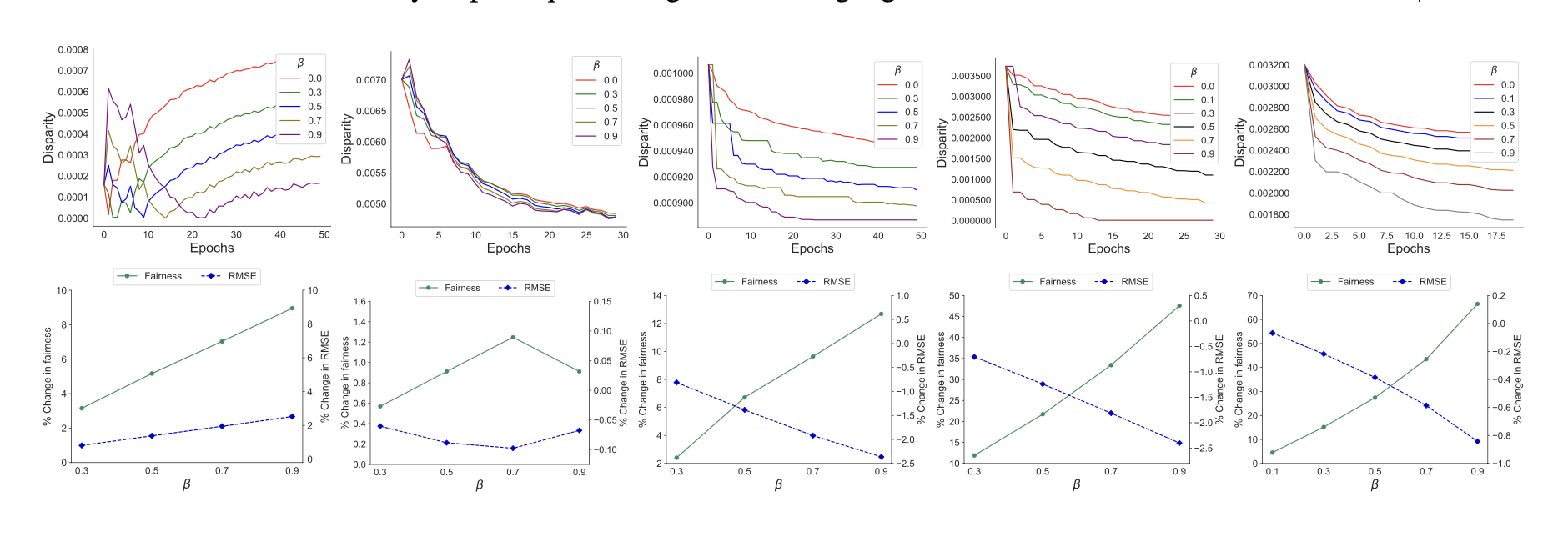
*Figure 3: Top: Disparity vs. epochs for different fairness budgets ($\beta$). Bottom: % change in fairness and RMSE with varying $\beta$.
Privacy-Utility Trade-off: Varying LDP mechanism parameters, such as noise variance ($\lambda$), demonstrated a balance between privacy and utility. While higher $\lambda$ increased privacy through noise, it slightly raised RMSE. Proper tuning of $\lambda$ and the clipping threshold ($\delta$) allowed for effective privacy protection with minimal utility loss.

*Figure 4: Privacy budget ($\epsilon$) and personalization RMSE under varying $\delta$ and $\lambda$.
5.4.1 Analysis of Results-
Fairness vs. Utility: F2PGNN improves fairness significantly while maintaining high utility. Its flexible fairness budget ($\beta$) enables tailored prioritization of fairness or accuracy, making it practical for industries requiring both.
-
Privacy Protection: The integration of LDP safeguards sensitive user data (e.g., gender, activity) while preserving utility. This demonstrates that privacy, fairness, and utility can be effectively balanced in federated learning setups.
6. Conclusion
6.1 SummaryThis paper introduces F2PGNN, a groundbreaking framework that integrates fairness into federated GNN-based recommendation systems (RSs) while safeguarding user privacy. By employing GNNs alongside a fairness-aware loss function, the framework mitigates demographic biases without accessing sensitive user attributes. Additionally, it uses Local Differential Privacy (LDP) to protect model updates and group statistics, ensuring compliance with privacy regulations.
6.2 Key Contributions-
Fair Federated GNNs: F2PGNN is the first framework to address fairness in federated GNN-based RSs, significantly reducing group disparity and ensuring equitable treatment across demographic groups.
-
Privacy-Preserving Techniques: Leveraging LDP for both model updates and group statistics, F2PGNN complies with stringent privacy regulations, making it suitable for applications where privacy is critical.
-
Practical Effectiveness: The framework demonstrates substantial fairness improvements with minimal utility loss, proving scalable and adaptable to large datasets. Its ability to incorporate various sensitive attributes, such as gender and activity levels, enhances its practical applicability.
Despite its advancements, F2PGNN has a few limitations:
- Privacy-Utility Trade-off: The use of LDP introduces noise, which can slightly reduce recommendation accuracy. Further research is needed to optimize this balance.
- Scalability Challenges: Its performance on highly heterogeneous or large-scale federated networks remains untested, limiting applicability to certain real-world systems.
- Bias Generalization: While effective for specific fairness metrics, the framework’s ability to address diverse fairness definitions, such as intersectional biases, requires further investigation.
Author Information
-
Qiuli Jin
-
Affiliation: KAIST, Human Factors and Ergonomics Lab
-
Research Topics: Virtual Reality; Data science
7. References
[1] Gupta, Manjul, Carlos M. Parra, and Denis Dennehy. “Questioning racial and gender bias in AI-based recommendations: Do espoused national cultural values matter?.” Information Systems Frontiers 24.5 (2022): 1465-1481.
[2] Himeur, Yassine, et al. “Latest trends of security and privacy in recommender systems: a comprehensive review and future perspectives.” Computers & Security 118 (2022): 102746.
[3] Kairouz, Peter, et al. “Advances and open problems in federated learning.” Foundations and trends® in machine learning 14.1–2 (2021): 1-210.
[4] Wu, Chuhan, et al. “A federated graph neural network framework for privacy-preserving personalization.” Nature Communications 13.1 (2022): 3091.
[5] Lyu, He, et al. “Advances in neural information processing systems.” Advances in neural information processing systems 32 (2019): 1049-5258.
[6] Li, Yunqi, et al. “User-oriented fairness in recommendation.” Proceedings of the web conference 2021. (2021): 624-632.
[7] Chai, Di, et al. “Secure federated matrix factorization.” IEEE Intelligent Systems 36.5 (2020): 11-20.
[8] Wu, Shiwen, et al. “Graph neural networks in recommender systems: a survey.” ACM Computing Surveys 55.5 (2022): 1-37.
8. Additional Materials
-
Paper Link: Access the full paper on arXiv.
-
GitHub Implementation: Explore the implementation of F2PGNN on GitHub.