[NeurIPS-22] Interaction Modeling with Multiplex Attention
1. Problem Definition
실제 세계에서는 교통 시스템, 팀 스포츠, 분자운동 등 다양한 유형의 multi-agent system이 존재합니다. 이러한 multi-agent system에서는 각 개체가 독립적으로 움직이지 않고 다른 개체들과 상호작용을 통해 영향을 주고받으면서 움직이게 되는데요. 이 때 개체 간의 상호작용을 명시적으로 모델링하는 것은 system의 복잡한 dynamics를 이해하는 데에 도움을 줄 수 있는 중요한 작업입니다. 이 논문에서는 multi-agent system에서 개체 간의 상호작용을 multiplex graph의 형태로 모델링하는 self-supervised learning framework를 제안합니다.
2. Motivation & Proposed Idea
상호작용 모델링의 어려운 점 중 하나는 상호작용 구조에 대한 정답이 존재하지 않는다는 점입니다. 도입부에서 예시로 든 multi-agent system들에서도 각 개체의 시점별 정보(위치 등)는 데이터로 존재하지만, 일반적으로 개체와 개체 간의 관계는 명시적으로 정의하기 어려운 정성적인 정보이기 때문에 label이 존재하지 않습니다. 따라서, 본 논문을 비롯한 주요 선행 연구들에서는 개체 간 상호작용에 대한 정보를 label로 주고 모델을 학습하는 것이 아니라, self-supervised learning을 통해 움직임 데이터만을 기반으로 개체 간 상호작용 구조를 graph 형태로 추론하는 방식을 택하고 있습니다.
또 다른 어려움은 개체 간 상호작용의 방식이 여러 가지일 수 있다는 점입니다. 실제 환경에서 개체들은 단일한 방식으로만 상호작용하는 것이 아니라, 다양한 방식으로 동시에 상호작용할 수 있습니다. 예를 들어, 축구 경기에서 한 선수는 동시에 여러 선수들과 패스, 탈압박, 위치적 협력 등 다양한 상호작용을 합니다. 이런 복합적인 상호작용을 효과적으로 모델링하기 위해서는 multiplex graph와 같이 하나의 node pair에 대하여 여러 종류의 관계를 동시에 표현할 수 있는 구조가 필요합니다. 따라서 본 논문에서는 개체 간 관계를 단일 graph가 아닌 여러 개의 layer를 갖춘 multiplex graph 형태로 모델링해야 한다고 주장합니다.
그러나 기존의 선행 연구[1-4]들은 이러한 상호작용을 각 node pair에 대한 edge-type classification task로 단순화하는 경향이 있었습니다. 즉, 주어진 시스템에서 가능한 상호작용의 유형(edge type)이 A, B, C라면, 기존 연구는 각 개체의 pair가 하고 있는 상호작용의 유형을 이 중 하나로 분류하도록 학습을 진행합니다. 이 방식은 일부 문제에서는 효과적일 수 있지만, 같은 개체의 pair 간에 여러 유형의 상호작용이 동시에 존재할 수 있는 실제 세계의 많은 multi-agent system에는 적용이 어려울 수 있습니다. 위에서 언급한 축구를 다시 예로 들면, 공을 잡은 선수와 각각의 팀 동료에 대한 상호작용을 모델링할 때 특정 동료가 패스를 보내려는 대상이면서 동시에 선수가 직접 접근하고자 하는 대상이 될수도 있습니다.
이런 한계를 극복하기 위해 본 논문에서는 multiplex graph latent structure를 가지고 있는 Interaction Modeling with Multiplex Attention (IMMA) 과 IMMA를 효과적으로 학습하는 기법인 Progressive Layer Training (PLT) 을 제안합니다. IMMA의 결과로 얻어지는 multiplex latent graph의 여러 layer는 서로 다른 상호작용 방식을 표현하며, 이들은 서로 독립적으로 학습되므로 한 node pair가 여러 layer에 대해서 높은 connectivity를 가질 수 있습니다. PLT는 curriculum learning [5]과 유사하게 여러 단계로 나누어 학습을 진행하는 방식으로, 먼저 single-layer latent graph를 학습하여 가장 주요한 상호작용 정보가 추출되도록 한 후, 해당 layer의 weights를 고정한 채 새로운 layer를 추가하여 더 복잡한 상호작용을 학습하도록 network를 확장합니다. 논문에서는 IMMA와 PLT를 통하여 개체 간의 복잡한 관계를 multiplex graph의 형태로 효과적으로 모델링할 수 있다고 이야기하고 있습니다.
3. Method
이제 논문에서 novel points로 제안하고 있는 IMMA와 PLT에 대하여 구체적으로 설명해 드리겠습니다.
Interaction Modeling with Multiplex Attention
IMMA의 목표는 여러 개체들의 이동 궤적을 보고 이들 간의 관계를 나타내는 multiplex graph를 self-supervised learning 방식으로 추론하는 것인데요. 이를 위하여 아래 작업을 수행하는 encoder와 decoder 구조를 사용합니다.
-
Encoder: 개체들의 현재까지의 이동 궤적을 입력으로 받아서 이들 간의 관계를 multiplex graph 형태로 추론합니다. 추론된 multiplex graph는 행/열이 모두 개체의 집합이고 edge weight가 0 이상 1 이하인 K개의 adjacency matrix들로 구성되어 있습니다. 즉, ‘개체들이 이렇게 움직이는 것을 보니 이들 사이에는 이런 관계가 있겠구나’ 라고 추론합니다. (아래 그림에서 왼쪽을 보고 오른쪽을 ‘infer’)
-
Decoder: 개체 간의 관계를 설명하는 multiplex graph를 보고 각 개체의 미래 궤적을 예측합니다. 즉, ‘개체들 간에 이런 관계가 있는 것을 보니 다음 시점에 이들이 이렇게 움직이겠구나’ 라고 예측합니다. (아래 그림에서 오른쪽을 보고 왼쪽을 ‘predict’)
학습은 decoder가 내뱉는 개체의 예측 궤적과 실제 궤적을 비교하여 진행됩니다. 그렇게 되면 개체 간의 관계를 명시적으로 정답으로 주지 않아도 다음 시점의 움직임을 예측하는 과정에서 내재된 관계를 추론할 수 있는 것이죠. GPT [6]에서 다음 단어 예측을 할 때 과거의 어떤 단어가 예측에 영향을 미쳤는지 추론하는 과정과 유사하다고 볼 수 있겠습니다.

좀 더 세부적으로 설명하자면, 시점 t에 대한 N개 개체의 feature vector를 $\mathbf{x}^t = \lbrace \mathbf{x}^t_ 1, \ldots, \mathbf{x}^t_ N \rbrace$라고 하면(즉, $\mathbf{x}^t_ i$는 시점 t에 대한 개체 i의 feature vector), 모델은 과거 시점의 궤적 $X^{1 : T_ h} = \lbrace \mathbf{x}^{1 : T_ h}_ i \vert i = 1, \ldots, N \rbrace$를 입력으로 받아서 미래 시점의 궤적 $X^{T_ h + 1 : T_ h + T_ f} = \lbrace \mathbf{x}^{T_ h + 1 : T_ h + T_ f}_ i \vert i = 1, \ldots, N \rbrace$를 예측하는 task를 수행하게 됩니다. 그 과정에서 latent graph $\mathbf{z} = (z_ {ij})_ {i,j=1}^N$를 학습하게 되며, 이 때 각 $z_ {ij} = (z_ {ij}^1, \ldots, z_ {ij}^K)$는 각 component가 0 이상 1 이하의 실수인 K차원 벡터입니다.
학습 단계에서 IMMA는 기본적으로 Conditional Variational Autoencoder (CVAE) [7, 8]의 방식을 따릅니다. 전체 시점의 궤적을 보고 latent graph를 추론하는 encoder (posterior) $q_ {\phi} (\mathbf{z} \vert \mathbf{x}^{1 : T_ h + T_ f})$ 및 과거의 궤적과 latent graph를 보고 미래 궤적을 추론하는 decoder (likelihood) $p_ {\theta} (\mathbf{x}^{T_ h+1 : T_ h + T_ f} \vert \mathbf{x}^{1 : T_ h}, \mathbf{z})$에 대하여 아래의 CVAE loss를 줄이는 방식으로 학습이 진행됩니다.
$\mathcal{L}(\theta, \phi) = -\mathbb{E}_ {q_ {\phi} (\mathbf{z} \vert \mathbf{x}^{1 : T_ h + T_ f})} \left[ \log p_ {\theta} (\mathbf{x}^{T_ h+1 : T_ h + T_ f} \vert \mathbf{x}^{1 : T_ h}, \mathbf{z}) \right] + D_ {KL} (q_ {\phi}(\mathbf{z} \vert \mathbf{x}^{1 : T_ h + T_ f}) \Vert p(\mathbf{z}))$
여기서 첫 번째 term은 reconstruction error로서 decoder가 출력하는 확률분포로부터 정답 궤적이 발생할 확률(likelihood)이 높아지도록 하는 역할을 합니다. 또한, 두 번째 term은 regularization error로서 posterior 분포 $q_ {\phi} (\mathbf{z} \vert \mathbf{x}^{1 : T_ h + T_ f})$와 (미래 궤적을 보지 않는) prior 분포 $p(\mathbf{z})$가 비슷해지게 하는 역할을 합니다. 이 과정을 거치면 validation이나 test 시 encoder에서 posterior 대신 사용되는 prior가 미래 움직임 정보 없이도 그럴 듯한 latent graph를 출력하게 됩니다.
하지만 일반적인 CVAE 또는 상호작용 추론 관련 선행 연구에 대하여 IMMA는 아래와 같은 구조적 차별점을 가집니다.
-
일반적인 CVAE의 encoder는 각 개체 i마다 agentwise latent vector $\mathbf{z}_ i$를 출력하지만, IMMA를 비롯한 neural relational inference 계열 선행 연구들은 encoder가 pairwise latent graph $\mathbf{z} = ( z_ {ij} )$를 출력하여 개체 간의 관계가 명시적으로 표현되도록 했습니다.
-
Pairwise latent graph를 출력하는 관련 선행 연구들은 상호작용을 edge-type classification 형태로 처리했기 때문에, node pair 별로 $\sum^K_ {k=1} z^k_ {ij} = 1$이 됩니다. 하지만, IMMA에서는 서로 다른 graph layer는 후술할 PLT로 독립적으로 학습하고, 한 layer 안에서 각 node에 연결된 edge outputs에 softmax를 적용함으로써 결과값이 (각각의 graph layer k 및 node i에 대해서) $\sum_ {j \in N_i} z^k_ {ij} = 1$을 만족하게 됩니다. 이 방식은 실제 세계에서 발생할 수 있는 복합적인 상호작용을 표현하기에 더 적합한데요. 예를 들어, 축구 선수들의 상호작용을 표현하는 multiplex graph에서 $z^1_ {ij}$가 ‘i가 공을 잡았을 때 j에게 패스를 줄 확률’을 나타내고 $z^2_ {ij}$가 ‘i가 j에게 접근할 확률’을 나타낸다고 합시다. 기존 방법에서는 $z^1_ {ij}, z^2_ {ij}$ 중 하나만 1에 가까워야 한다는 제약이 생기는데, 실제로는 i가 j에게 패스를 줄 가능성과 j에게 접근하고 있을 가능성이 모두 높을 수 있습니다. 오히려 j에게 패스를 주거나 접근할 확률이 높다면 다른 선수들에게 패스를 주거나 접근할 확률이 낮다는 뜻이므로 IMMA의 세팅처럼 i의 neighbors $N_i$들에 대해서 $\sum_ {j \in N_i} z^k_ {ij} = 1$이 되는 것이 더 합리적입니다.
-
Decoder에서 GraphGRU [9]를 사용하여 graph 구조를 반영하면서 sequential prediction을 수행했습니다. GraphGRU는 시계열 데이터를 다루기 위해 고안된 neural network인 Gated Recurrent Units [10]에 graph 구조를 합친 것으로, 각 개체에 대하여 다음 시점의 hidden state $\tilde{\mathbf{h}}^{t+1}_ j$를 산출할 때 직전 시점의 자기 자신의 hidden state $\tilde{\mathbf{h}}^{t}_ j$ 뿐 아니라, latent graph $\mathbf{z}$ 구조를 참고하여 모든 개체의 직전 시점 hidden state $\tilde{\mathbf{h}}^{t}$로부터 message passing 형태로 적절한 정보를 가져옵니다. 마지막으로 hidden state를 위치 변화로 decode 해주는 readout MLP $f_ {\text{out}}$을 도입하여 다음 시점의 개체의 위치 변화를 예측합니다.
$\tilde{\mathbf{h}}^{t+1}_ j = \text{GraphGRU}(\tilde{\mathbf{h}}^{t}_ j, \tilde{\mathbf{h}}^{t}, \mathbf{z}), \quad \hat{\mathbf{x}}^{t+1}_ j = \hat{\mathbf{x}}^{t}_ j + f_ {\text{out}} (\tilde{\mathbf{h}}^{t+1}_ j)$
아래 그림에 IMMA의 전체적인 모델 구조가 나와 있습니다. Encoder 및 decoder에서 다른 개체의 feature vector 또는 hidden state를 참조하기 위하여 GNN의 message passing 구조를 도입했는데, 이에 대한 자세한 내용이 궁금하시다면 논문의 Appendix B를 참고해 주시기 바랍니다.
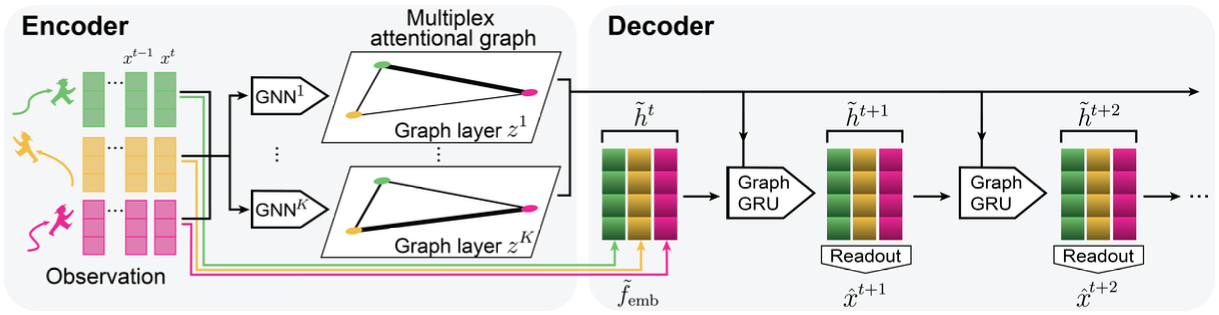
Progressive Layer Training
IMMA는 선행 연구 모델과 달리 서로 다른 graph layer 간에 softmax 등의 의존성이 걸려 있지 않기 때문에, 각 graph layer를 서로 다른 시점에 학습할 수 있습니다. 그래서 논문에서는 학습을 여러 단계로 나누어서 한 번에 하나의 graph layer에 대해서만 학습이 진행되도록 하는 PLT 방식을 제안했습니다. PLT에서는 먼저 single-layer latent graph를 학습하여 가장 주요한 상호작용 정보가 추출되도록 한 후, 해당 graph layer의 weights를 고정한 채 새로운 layer를 추가하여 더 복잡한 상호작용을 학습하도록 네트워크를 확장합니다. 이러한 학습 방식은 먼저 상대적으로 쉬운 문제를 통해 기본적인 패턴을 학습함으로써 나중에 더 복잡한 패턴을 쉽게 배울 수 있도록 돕는 curriculum learning [5]에서 영감을 받았다고 하는데요. 이렇게 K개의 graph layer를 단계별로 나누어 학습함으로써 기본적인 상호작용부터 복잡한 상호작용까지 안정적으로 학습이 가능하고, 가장 중요한 latent graph layer가 어떤 것인지를 알 수 있으니(먼저 학습된 graph layer일수록 더 중요하겠죠?) 해석 가능성도 확보하게 됩니다.
이 때 hyperparameter K를 얼마로 설정하는지에 따라 얼마나 복잡하고 추상적인 상호작용까지 모델링을 할지가 결정되므로, 모델링하고자 하는 데이터에 대한 도메인 지식을 기반으로 K를 결정하면 됩니다. 다만, PLT의 특성상 뒤에 학습되는 graph layer는 앞서 학습된 graph layer에 영향을 미치지 않기 때문에, K의 개수가 결과에 큰 영향을 미치지는 않습니다. (즉, K=4일 때 1–3번째로 학습된 graph layer의 값은 K=3일 때 1–3번째로 학습된 graph layer 값과 완전히 동일합니다. 4번째 graph layer가 학습될 때에는 앞선 3개 layer를 산출하는 encoder weights가 고정되기 때문이죠.)
4. Experiment
논문에서는 다양한 multi-agent system에서 IMMA 모델의 성능을 평가하는 실험을 통해서 (1) 예측된 미래 궤적이 정확한지와 (2) 추론된 latent graph가 실제 관계를 잘 대변하는지의 두 관점에서 성능을 평가하고자 했습니다.
Experiment setup
Datasets: 논문에서는 SNE, PHASE, NBA datasets의 3가지 환경을 실험에 사용했습니다. 모든 실험에서 IMMA는 24개 시점 동안 개체들의 움직임을 관찰하고, 미래 10개 시점에 대한 개체의 움직임을 예측하는 방식으로 학습되었습니다. 아래 그림에서 PHASE와 NBA dataset에 대한 예시를 참고하세요.

-
SNE (Social Navigation Environment): 2D 평면에서 여러 개체가 서로 충돌하지 않도록 움직이는 상황을 모델링한 시뮬레이션 환경입니다. 각 개체는 특정 target friend를 만나기 위해 이동해야 하며, 그 과정에서 다른 개체와의 충돌을 피하기 위해 경로를 조정하게 됩니다.
-
PHASE (Pedestrian and Human Activity Simulation Environment) dataset: 2D 평면에서 두 개체가 두 개의 공과 상호작용하면서 움직이는 시뮬레이션 환경이며, 두 개체는 서로 협력하여 둘 중 하나의 공을 정해진 목적지까지 옮겨야 합니다.
-
NBA (The National Basketball Association) dataset: 실제 미국 프로농구 리그인 NBA 경기에서 취득한 데이터로, 매 0.4초마다(즉, 2.5Hz) 각 선수와 공의 위치가 기록되어 있습니다.
Baselines: 논문에서는 다양한 baseline을 실험에 사용했는데요. 이 중 주요 baseline을 몇 개만 소개해 보겠습니다.
-
MLP: 모든 개체의 모든 시점의 위치를 concatenate해서 만들어진 하나의 긴 feature vector를 입력으로 받는 naive baseline
-
GAT-LSTM: Graph Attention Network (GAT) [11] 기반으로 각 개체의 시점별 features를 node embedding으로 인코딩 후, LSTM으로 시점별 node embedding을 처리하는 네트워크
-
NRI [1]: Recurrent GNN을 기반으로 하는 VAE 모델 (Graph Convolutional Network (GCN) [12]의 저자 Thomas Kipf와 Max Welling이 발표한 이 분야의 가장 중요한 선행 연구입니다.)
-
RFM [9]: NRI와 유사한 구조를 사용하지만, ground truth relational graph을 보고 supervised learning 방식으로 학습되는 모델
-
IMMA-SG: Encoder가 출력하는 latent graph를 single layer로 구성한 IMMA
-
IMMA-MG: 논문에서 제안하는 multiplex latent graph 기반의 IMMA. (PLT를 적용하지 않고 모든 graph layer를 한 번에 학습했을 때와 PLT를 적용해서 한 번에 하나의 graph layer를 학습했을 때의 성능을 비교합니다.)
Evaluation metrics: 실험에서는 아래의 evaluation metric 들을 통해 (1) 예측 궤적의 정확도(ADE & FDE)와 (2) 추론된 latent graph의 유효성(graph accuracy)을 비교평가하고자 했습니다.
-
ADE (average displacement error): 예측 궤적과 실제 궤적간 평균 오차
-
FDE (final displacement error): 마지막 시점의 예측 위치와 실제 위치간 오차
-
Graph accuracy: 내재된 관계에 대한 ground truth가 존재하는 SNE와 PHASE에 대해서, 정답 graph와 모델이 추론한 graph의 유사도(물론, 학습시에는 ground-truth graph가 사용되지 않습니다.)
Results
먼저, (1) 예측 궤적의 정확도 측면에서는 논문에서 제안하는 IMMA가 다른 baseline보다 전반적으로 작은 오차(ADE & FDE)를 보입니다. Single latent graph를 사용하는 IMMA-SG의 경우 SOTA인 EvolveGraph, RFM, fNRI 등보다 성능이 낮은 경우도 있지만, multiplex latent graph를 사용하고 이를 PLT 방식으로 학습하게 되면(MG + PLT) 성능이 큰 폭으로 향상되어 SOTA baseline들의 성능을 크게 앞지르게 됩니다. 이 결과는 개체 간의 복합적인 상호작용을 multiplex graph로 잡아내는 것과 PLT로 이를 단계적으로 학습하는 것이 유의미하다는 것을 보여주고 있습니다.
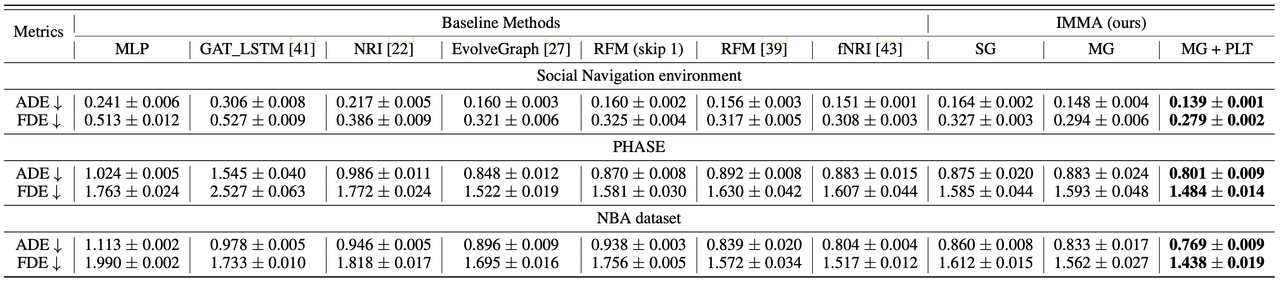
다음 표를 보면, (2) 추론된 latent graph의 유효성 측면에서도 IMMA가 추론한 latent graph가 baseline들의 결과보다 훨씬 높은 graph accuracy를 달성함을 확인할 수 있습니다. Single latent graph를 사용하기만 해도 SOTA baseline과의 graph accuracy 차이가 10% 이상 나는 것을 보면, IMMA의 구조 자체가 개체 간에 내재된 상호작용을 잡아내는 데에 적합하다고 볼 수 있겠습니다.

다음 그림에서는 5개의 개체가 각각 다른 개체 중 하나를 쫓아가는 SNE에서 true latent graph와 모델들이 추론한 latent graph를 비교하여 보여줍니다. 가장 왼쪽의 ground truth가 의미하는 것은 0, 1, 2, 3, 4번 개체가 각각 2, 2, 3, 4, 3을 만나기 위해 이동하는 상황임을 보여줍니다. IMMA는 개체들의 과거 움직임(observed trajectories)만 보고 미래 움직임(predicted trajectories)을 예측하는 동시에, 각 개체가 어떤 개체를 쫓고 있는지에 대한 정보를 상당히 정확하게 추론하고 있음을 확인할 수 있습니다. 반면 RFM은 학습시 true latent graph를 보고 supervised learning을 진행했음에도 불구하고 내재된 상호작용을 잘 추론하지 못하는 것을 보여줍니다.

5. Conclusion
이 논문은 multi-agent system에서 개체 간의 상호작용을 효과적으로 추론하기 위한 모델인 IMMA를 제안합니다. IMMA는 학습시 상호작용을 표현하는 true latent graph가 주어지지 않아도, 개체의 미래 궤적을 예측하는 과정에서 각 개체가 어떤 개체에게 영향을 받아서 움직이고 있는지를 attention 기반의 self-supervised learning 방식으로 학습합니다. 특히, 기존의 상호작용 모델들이 다양한 상호작용의 중첩을 제대로 처리하지 못하는 것과 달리, IMMA는 복수의 독립적인 상호작용을 나타내기 위해 multiplex graph 구조를 활용하여 움직임 예측 성능과 추론된 상호작용의 해석 가능성을 모두 개선했습니다.
다만, 이 연구의 가장 큰 한계점은 개체 간의 관계가 시간에 따라 변하지 않는다고 가정하고, 주어진 시스템에 대하여 고정된 latent graph를 추론한다는 점입니다. 하지만, 실제 세계의 많은 multi-agent system에서 개체들의 상호작용 양상은 시간이 지나면서 바뀔 수 있습니다. 예를 들어, A라는 개체가 처음에는 B를 쫓다가 목표를 바꿔서 C를 쫓아다니게 될 수 있는 것이죠.
현재 제가 주력하고 있는 도메인은 축구 데이터 분석인데, 실제 프로축구 팀에서 전술 분석을 위하여 시점별로 어떤 선수가 어떤 선수를 마크하고 있는지를 자동으로 찾고자 하는 수요가 있습니다. 이 정보로부터 전술 코치는 팀이 효과적인 맨마킹에 실패해서(즉, 아무도 쫓아다니지 않는 상대 팀 공격 선수가 생겨서) 실점 위기를 초래한 장면을 자동으로 검출하거나, 4-3-3 포메이션을 상대할 때 우리 팀이 어떤 전술을 사용해야 대부분의 시간 동안 효과적으로 상대를 마크할 수 있을지 등을 파악할 수 있을 것입니다. 그래서 저는 이 연구를 발전시켜서 시간에 따라서 변하는 상호작용을 모델링할 수 있는 self-supervised learning framework를 만들고, 이를 축구 경기에서 선수들의 움직임 데이터에 적용하여 시점별로 누가 누구를 수비하고 있는지, 그리고 누가 누구와 협력하고 있는지를 자동으로 찾는 모델을 개발해 볼 계획입니다. (관련하여 프리미어리그 노팅엄 포레스트 FC의 데이터 사이언티스트 Sean Groom이 Hidden Markov Model을 기반으로 코너킥 상황에서 이 task를 수행하는 선행 연구[13]를 발표했는데, 관심 있으신 분들은 참고하시기 바랍니다.)
아무쪼록 긴 글 읽어 주셔서 감사하고, 관련하여 궁금한 점이 있거나 아이디어를 나누고 싶으신 분들은 아래 연락처로 문의 부탁드립니다.
Author Information
Hyunsung Kim (20245495)
Ph.D. student at Data Science & Artificial Intelligence Lab, KAIST
-
Email: hyunsung.kim@kaist.ac.kr
-
Research interests: sports analytics, machine learning, graph neural networks
References & Additional Materials
-
Github implementation: https://github.com/sunfanyunn/IMMA.git
-
References:
-
Thomas N. Kipf, Ethan Fetaya, Kuan-Chieh Wang, Max Welling, and Richard S. Zemel. Neural relational inference for interacting systems. In International Conference on Machine Learning (ICML), 2018.
-
Changan Chen, Sha Hu, Payam Nikdel, Greg Mori, and Manolis Savva. Relational graph learning for crowd navigation. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2020.
-
Colin Graber and Alexander Schwing. Dynamic neural relational inference for forecasting trajectories. In IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2020.
-
Jiachen Li, Fan Yang, Masayoshi Tomizuka, and Chiho Choi. Evolvegraph: Multi-agent trajectory prediction with dynamic relational reasoning. Advances in Neural Information Processing Systems (NeurIPS), 2020.
-
Yoshua Bengio, Jérôme Louradour, Ronan Collobert, and Jason Weston. Curriculum learning. In International Conference on Machine Learning (ICML), 2009.
-
Alec Radford, Karthik Narasimhan, Tim Salimans, and Ilya Sutskever. Improving language understanding by generative pre-training. 2018.
-
Diederik P. Kingma and Max Welling. Auto-encoding variational Bayes. 2013.
-
Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning structured output representation using deep conditional generative models. In Advances in Neural Information Processing Systems (NeurIPS), 2015.
-
Andrea Tacchetti, H. Francis Song, Pedro A. M. Mediano, Vinicius Zambaldi, János Kramár, Neil C. Rabinowitz, Thore Graepel, Matthew Botvinick, and Peter W. Battaglia. Relational forward models for multi-agent learning. In International Conference on Learning Representations (ICLR), 2019.
-
Kyunghyun Cho, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Conference on Empirical Methods in Natural Language Processing (EMNLP). 2014.
-
Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. In International Conference on Learning Representations (ICLR), 2018.
-
Thomas N. Kipf and Max Welling. Semi-Supervised Classification with Graph Convolutional Networks. In International Conference on Learning Representations (ICLR), 2017.
-
Sean Groom, Dan Morris, Liam Anderson, and Shuo Wang. Modeling defensive dynamics in football: A Hidden Markov Model-based approach for man-marking and zonal defending corner analysis. In IJCAI Workshop on Intelligent Technologies for Precision Sports Science (IT4PSS), 2024.