Aug. 4th, 2023 Conference: KDD(Knowledge Discovery and Data Mining), 2023 논문_Link

1. Problem Definition

  • 도시에 필수적인 전기, 도로, 통신 등의 인프라는 상호 의존적 네트워크를 형성하며, 결과적으로 하나의 인프라에서 발생하는 변화 및 사고가 다른 인프라에도 영향을 미침.
  • 자연 재해나 기술적 문제로 특정 인프라가 손상될 경우, 그 피해는 해당 인프라에만 국한되지 않고 연결된 네트워크 전체에 연쇄적으로 확산될 가능성 존재.
  • 이러한 도시 인프라 네트워크 간 손상 전파는 21세기 현재도 발생하고 있어, 이에 대한 실질적 피해를 야기 (뉴 올리언즈 2024, 영국, 2019 등).

Figure 1. 전력망 손상으로 인한 교통망 마비의 사례 - 영국 2019년.

  • 추후 차량간 통신을 매개로 도로망과 통신망 간 연결, 통신망을 통한 전력 그리드의 자동화 관리 등 도시 인프라 네트워크 간 연결성은 강화될 전망임.
  • 연쇄적인 피해를 줄이기 위해 인프라 네트워크 내 취약한 노드를 식별, 해당 노드가 손상될 경우 발생할 수 있는 위험을 미리 예측 및 관리할 필요 있음.
  • 본 연구는 도로망과 전력망의 상호 의존적 관계를 바탕으로, 데이터 기반 접근을 통해 취약한 노드를 식별하고, 도시 인프라의 취약성을 분석하여 연쇄적 피해를 줄이는데 기여할 수 있는 방법론을 제시 함.

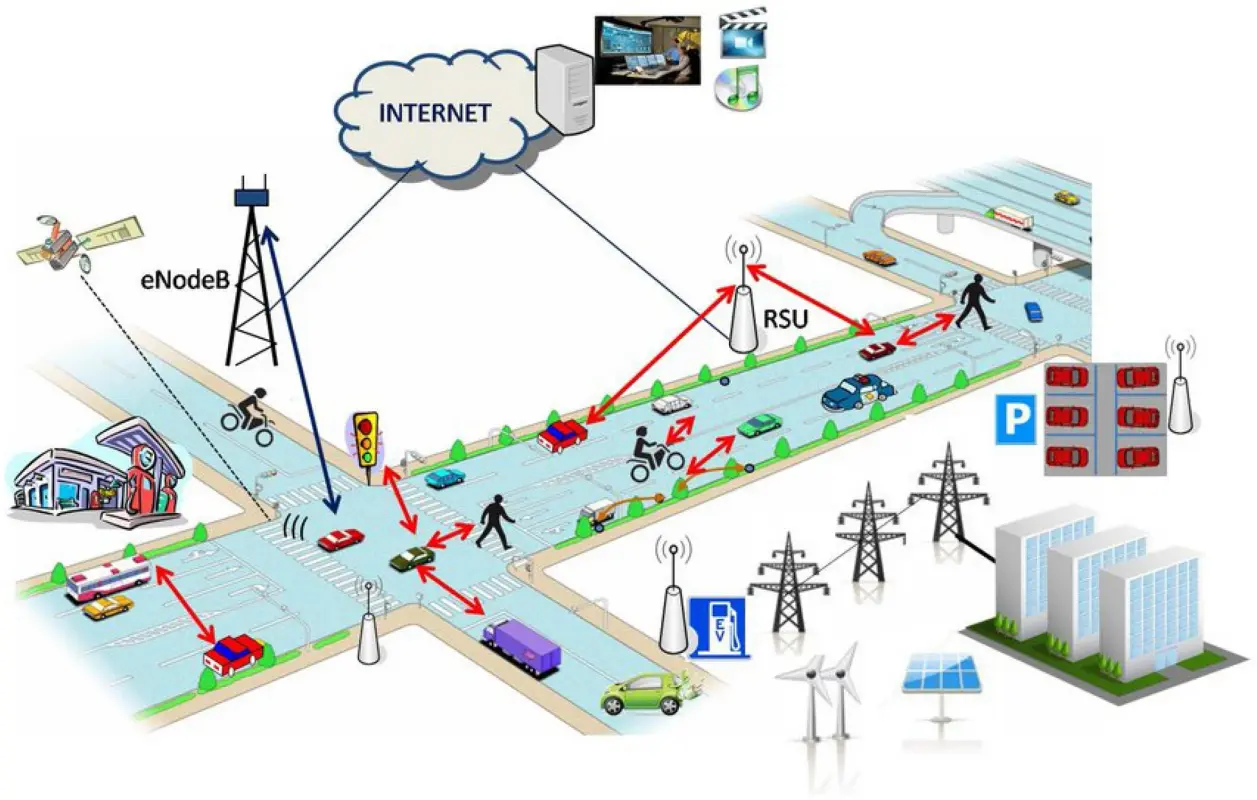
Figure 2. 전기, 도로, 통신 등 도시 인프라 간 상호 의존에 대한 개념도.
※ 도시 인프라 간 상호의존성은 물리적 및 직접적 연결성에 국한되지 않음. 상기 Fig. 2.의 예에서는 도로망과 전력망은 신호등을 통해 연결하고 있으며, 통신망 또한 신호등을 통해 도로망 및 전력망과 연결을 취하고 있음. 본 예시에서, 전력망 또는 통신망의 피해로 인해 신호체계가 오/미작동 할 경우 이로 인해 도로망의 마비 등을 야기할 수 있음.

2. Motivation

2-1. 전통적 접근의 한계

  • 기존 취약성 분석 방법은 주로 도메인 지식을 갖춘 전문가 집단 또는 특정 기능 공학(feature engineering)을 활용한 방식에 의존하고 있음. 이는 인프라 네트워크의 개별적 요소들을 분석하는 데는 효과적이나, 인프라 간의 복잡한 상호 의존성이나 상호작용을 모델링하는 데는 한계를 보임.
  • 이러한 한계는 네트워크의 고차원적이고(상호 연결성) 이질적인 특성을 충분히 반영하지 못하기 때문에 발생.
  • 예를 들어; ㄱ) 도로망과 전력망 사이의 상호작용을 이해하려면 각각의 네트워크뿐 아니라 그들 간의 상호작용을 동시에 분석할 수 있어야 함. ㄴ) 각 개인의 역량에 의존하는 기존의 전문가 시스템의 경우, 대규모 및 다양한 유형의 (교통, 전력 등) 인프라를 동시에 고려하기에 현실적 한계가 존재. ㄷ) 기존의 규칙 기반 모델의 경우, 각 유형별 인프라 네트워크의 운영 및 인프라 간 접점에서의 복잡한 규칙을 단일 모델링 프레임워크에 구현 하는 것에 계산 자원 및 비용적 한계가 존재. ㄹ) 상기 기존 방법론의 한계로 인해, 직접적으로 연결된 인프라 간 피해 전파를 넘어선 간접적 전파를 모사하는데 한계 존재. ㅁ) 기존 방법론의 경우, 향후 강화 될 것으로 예상되는 도시 인프라 네트워크 간 연결에 대응하기 위해 필수적인 확장성에 큰 한계가 존재.

2-2. GNN 기반 취약 노드 분석의 장점

  • GNN은 네트워크에서 노드와 엣지 간의 관계를 학습하며, 각 노드의 속성뿐만 아니라 이웃 노드들의 속성 및 그들 간의 상호작용을 함께 고려할 수 있어, 도시 인프라 네트워크처럼 상호 의존적인 시스템의 분석에 특히 유용하게 활용 가능.
  • 특히 GNN의 semi-supervised 학습을 통해, 소량의 라벨링된 데이터만으로도 네트워크 전체의 노드 특성을 예측하고 분석할 수 있도록 함.
  • GNN과 강화학습(RL)을 결합, 인프라 네트워크의 연속적인 진화 메커니즘을 구현 하여, 네트워크가 손상되었을 때 시스템 전체에 미치는 영향을 보상(reward)으로 설정 함으로서 취약한 노드를 선택하는 과정을 최적화 가능. 이를 통해 상호 의존적인 대규모 인프라 네트워크에서 발생할 수 있는 복잡한 고차원적 손상 패턴을 효과적으로 학습 및 예측.

2-3. 도시 인프라 네트워크의 특성과 semi-supervised 학습 적용 가능성

  • 도시 네트워크에서는 노드들 사이에 명시적으로 연결되지 않은 간접적 상호작용 존재하는 것을 이용 (cascade relationship), 노드 간의 연결이 직접적으로 보이지 않더라도 네트워크의 위상(topology)과 주변 노드 간의 상호작용에서 관계 추정 가능. ※ 예컨데, 두 개의 발전소가 물리적으로 직접 연결되지 않았더라도, 전력 수요를 통해 상호작용할(발전용량 조절 등) 가능성을 유추 가능.
  • 이러한 유사성과 상관성은 supervised 학습에서 활용 가능한 pseudo-label 역할을 하며, 본 연구에서 세미-슈퍼바이즈드 학습의 기반 제공.
  • 네트워크 상의 노드 간 연결을 예측하는 문제를 링크 예측 문제로 변환 가능하며, positive-edge (observed for supervised) 및 negative-edge (not observed)의 형태로 구현.
  • 본 연구에서는, 상기 접근을 통해 일부 라벨링 데이터를 활용하여 복잡한 도시 네트워크를 구현함과 동시에, 명시되지 않은 도시 인프라 네트워크 간 간접적 상호작용 (cascade relationship)을 반영하도록 함.

3. Methodology

본 연구에서는 도시 인프라 네트워크에서 취약한 노드를 식별하기 위해 그래프 신경망(GNN)과 강화학습(RL)을 결합한 데이터 기반 방법론을 제안하고 있음. 이는 크게 1) 상호 의존적 네트워크의 그래프 표현, 2) 그래프 신경망을 통한 취약 노드 분석, 3) 강화학습 기반 취약성 예측 세 가지 주요 단계로 구성.

Figure 3. Illustration of the proposed system - 본 연구에서 제안한 GNN 및 강화학습 기반 모형 개요.

3-1. 상호 의존적 도시 인프라 네트워크의 그래프화

  • 도시 인프라 네트워크는 도로망, 전력망, 통신망과 같은 다양한 인프라들이 상호 의존적으로 연결되어 있는 복잡한 시스템으로, 이를 효과적으로 모델링하기 위해 각 인프라 네트워크를 그래프 $G = (V, E)$로 표현. ($V$: 네트워크의 노드 집합, $V = V_r \cup V_e$, $E$: 노드 간의 엣지 집합 $E = E_r \cup E_e \cup E’$)

  • 본 연구에서는 두 개의 서로 다른 네트워크, 전력망 $e$과 도로망 $r$을 대상으로 각 네트워크 내의 노드와 엣지를 연결하는 그래프를 구성하였으며, 각 네트워크는 그들 사이에 상호작용이 있는 coupled graph로 표현. ※ 전력망과 도로망은 교차로의 신호등과 저전압 발전소가 연결되는 관계를 상정.

    그래프 구성: 전력망은 트리 구조를 기반으로 220 kV, 110 kV, 10 kV의 발전소 레벨로 구성되며, 도로망은 여러 교차로와 도로를 연결한 네트워크로 표현. 두 네트워크는 저전압 발전소와 교차로에 위치한 신호등이 연결되어 있으며, 이들 간의 상호작용을 결합 엣지 $E’$로 표현.

    노드 상태: 각 도시 인프라 네트워크의 노드는 정상(normal), 손상(damaged), 비정상(invalid)의 세 가지 상태로 분류하며, 비정상은 연결된 다른 노드의 손상으로 인해 동작하지 않는 상태를 상정.

    결합 그래프 표현: 결합된 네트워크를 나타내기 위해, 전력망 $G^e$와 도로망 $G^r$이 하나의 통합된 그래프 $G = (V^r ∪ V^e, E^r ∪ E_e ∪ E’)$로 표현.

3-2. 그래프 신경망을 통한 취약 노드 분석

  • GNN은 네트워크 내 각 노드의 구조적 정보를 학습하고, 이를 바탕으로 네트워크의 취약 노드를 예측하는 데 사용.

  • 본 연구에서는 semi-supervised learning을 활용하여 GNN을 학습 시키며, 이 과정에서 네트워크 내의 일부 노드만 라벨링 된 상태에서 나머지 노드의 속성과 관계를 GNN이 예측하도록 학습.

    임베딩 초기화: 각 노드는 네트워크의 구조적 특성을 반영하는 초기 임베딩 값$(f_v)$을 가지며, 전력망과 도로망의 노드들이 서로 다른 임베딩 벡터로 설정. 이 임베딩 값들은 네트워크의 특성을 저차원 공간에서 표현하기 위해 학습.

    ※ 임베딩 초기화 $f_v =\begin{cases} f_{e_v}, & \text{if } v \in V_e \backslash f_{r_v}, & \text{if } v \in V_r \end{cases}$

    GNN 구조: GNN은 각 노드의 이웃 노드들의 임베딩을 종합하여 새로운 임베딩 벡터를 계산하는 방식으로 학습되며, 노드 $V$의 최종 임베딩 벡터는 주어진 깊이 $L$에서 해당 노드의 이웃 노드들이 가진 정보들을 평균하여 업데이트.

    ※ 이웃 노드 정보 집계 $h_l^{N(v)} = AGG\left( { h_l^u, \forall u \in N(v) } \right)$ ※ 임베딩 업데이트 $h_{l+1}^v = \sigma \left( W_l \cdot MEAN\left( { h_l^v, h_l^{N(v)} } \right) \right)$ ※ 최종적 노드 임베딩 $z_v \equiv h_L^v$

    링크 예측을 통한 학습: 이 연구에서는 링크 예측 문제에 기반하여 GNN을 학습시킴. 네트워크 내에서 실제로 연결된 노드들 간의 관계를 예측하기 위해, 존재하는 엣지와 존재하지 않는 엣지들로 양의 그래프$(G^p)$와 음의 그래프$(G^n)$를 구성하고, 두 그래프 간의 차이를 최소화하는 방식으로 GNN을 학습​.

    ※ 노드 임베딩을 활용, 연결 가능성 계산 $S(Z_v, G) = z_v^T \cdot z_u, \forall e_{vu} \in E$ ※ 링크 예측 손실함수 정의 $J_G(Z_v) = MEAN\left( \max\left(0, M - S(Z_v, G_p) + S(Z_v, G_n)\right) + \lambda | \Theta |^2 \right)$

3-3. 강화학습 기반 도시 인프라 취약성 예측

  • 본 연구에서 강화학습은 네트워크 내에서 취약한 노드를 선택하고, 그 선택된 노드가 네트워크에 미치는 영향을 평가하는 데 사용되며, 네트워크 내 취약한 노드를 찾기 위한 최적의 정책을 학습.

    마르코프 결정 과정(MDP): 상태 $S$는 네트워크 내 노드들의 현재 상태(정상, 손상, 비정상)를 나타내며, 행동 $A$는 취약한 노드를 선택하는 작업을 의미한다. 보상 $R$은 손상된 노드가 네트워크에 미치는 영향을 수치화한 값으로 정의.

    ※ 최초 상태정의 (노드 임베딩 $Z_v$) $s_1 = MEAN(Z_v)$ ※ Action ($A(V_k)$)를 통한 특정 노드의 손상 및 이에 대한 보상 $R(v_k) = \begin{cases} a_e P(v_k, G_e) + a_r A(E(v_k, G), G_e), &\text{if } v_k \in V_e \ a_r A(v_k, G_e), & \text{if } v_k \in V_r \end{cases}$ ※ Bellman 방정식을 활용한 각 Action의 가치 계산 $Q^\pi(s, v) = R(v) + \gamma \max_{v’} Q^\pi(s’, v’)$ ※ Action의 가치 및 ϵ-greedy 방식을 사용한 행동 선택 $v_k = \begin{cases} \text{최적 행동 (최대 Q값)}, & \text{확률 } 1 - \epsilon \ \text{무작위 행동}, & \text{확률 } \epsilon \end{cases}$

    Q-러닝 기반 정책 학습: Q-러닝 알고리즘을 사용하여 각 노드들의 상태에서 행동에 대한 가치를 예측하며, epoch마다 네트워크 손상 시 보상을 최대화하는 방향으로 정책을 업데이트.

    ※ Q 값에 기반하여, 행동 및 노드의 선택에 대한 가치 추정 $Q^\pi(s_ k, v_ k; \Theta) = MEAN((\theta_ 2 \cdot (\sigma(\theta_ 1 \cdot Z_ v)))^T \cdot [s_ k, \dots, s_ k]_ {\vert V \vert})$ ※ 손실 함수의 정의 및 손실 함수 최소화 지향 학습 $J_ Q(\Theta) = MEAN\left( \vert (r_ k + \gamma \max_v \hat{Q}(s_ {k+1}, v; \hat{\Theta})) - Q(s_ k, v_ k; \Theta) \vert^2 \right)$

    보상 함수 정의: 보상 함수는 선택된 노드가 네트워크의 전력망 및 도로망에 미치는 영향을 반영할 수 있도록 정의. 전력망의 손상은 감소된 전력량으로 산출하며, 도로망의 손상은 연결성의 감소로 산출됨. 이러한 두 요소는 보상 함수에 가중치 $a^e$와 $a^r$로 반영되어 취약한 노드를 선택하는 데 영향을 미침.

    ※ 보상 함수 정의 및 손상 최소화 $R(v_k) = \begin{cases} a_e P(v_k, G_e) + a_r A(E(v_k, G), G_e), & \text{if } v_k \in V_e \backslash a_r A(v_k, G_e), & \text{if } v_k \in V_r \end{cases}$

    $v_k$ : 선택된 노드
    $G_e$ : 전력망 그래프
    $G_r$ : 도로망 그래프
    $P(v_k, G_e)$ : 전력망에서 노드 $v_k$가 손상되었을 때의 전력 감소량
    $A(v_k, G_e)$ : 도로망에서 노드 $v_k$의 손상으로 인해 발생하는 연결성 감소량
    $E(v_k, G)$ : 노드 $v_k$의 손상이 영향을 미치는 다른 노드(예: 신호등) 집합
    $a_e, a_r$ : 전력망과 도로망의 상대적 중요도를 나타내는 가중치 계수

    취약 노드 선택 과정: 각 epoch마다 네트워크에서 노드를 선택, 그 노드가 손상되었을 때의 상태 변화를 관찰함. 이후, 선택된 노드가 네트워크 전체에 미치는 영향을 보상으로 설정하고, 최종적으로 취약한 노드를 선택하는 정책을 학습.

4. Experiment

본 연구에서는 도시 인프라 네트워크에서 취약한 노드를 식별하기 위해 제안된 GNN 및 강화학습 기반 방법론을 다양한 환경에서 평가함. 해당 실험은 주로 성능 비교, 전이 가능성 평가, 및 각 구성 요소의 유효성을 검증하는 데 중점을 두고 수행됨.

4-1. Experiment Setup

  • 본 실험은 도시 인프라의 상호 의존적 네트워크를 시뮬레이션한 환경에서 수행됨. 각 네트워크는 실제 데이터를 기반으로 하며, 상호 의존적 네트워크의 복잡성을 반영하도록 구성.

    전력망: 10,887개의 노드와 11,438개의 엣지를 가진 전력망을 사용하며, 고전압(220kV), 중전압(110kV), 저전압(10kV) 발전소로 구성된 트리 구조.

    도로망: 주요 도로망$(G^{rp})$은 1,035개의 노드와 1,161개의 엣지로 구성되며, 부차적 도로망$(G^{rt})$은 4,825개의 노드와 5,025개의 엣지를 포함.

    결합 네트워크: 전력망과 도로망이 상호 연결된 결합 네트워크$G = (V^r ∪ V^e, E^r ∪ E_e ∪ E’)$는 15,712개의 노드와 21,191개의 엣지를 포함하며, 전력망의 저전압 발전소와 도로망의 신호등 간의 상호작용을 구현.

  • 제안된 방법론의 성능을 평가하기 위해 하기 평가지표를 사용.

    전력망 성능 지표: 전력망에서 각 노드가 손상되었을 때 남은 전력량을 계산하여 시스템에 미치는 영향을 평가하며, 감소된 전력량을 통해 전력망의 취약성을 측정.

    도로망 성능 지표: 도로망의 연결성 감소 비율(Connectivity Ratio)과 거대 연결 구성 요소(Giant Connected Component, GCC)의 크기를 측정하여, 도로망의 노드 손상에 따른 연결성 변화를 평가.

    결합 네트워크 보상: 전력망 및 도로망의 손상 정도를 보상으로 계산하여, 상호 의존적 네트워크에서의 성능을 종합적으로 평가하며, 전력망의 전력 손실과 도로망의 연결성 손실을 반영하여 보상값을 계산.

  • 제안된 GNN 및 강화학습 기반 방법론을 기존의 전통적인 방법들과 비교하여 그 성능을 평가하였으며, 비교 대상이 된 전통적 방법론들은 아래와 같음.

    차수 기반 선택법(Degree-Based): 노드의 차수를 기준으로 취약 노드를 선택.

    집합 영향력(Collective Influence, CI): 네트워크 내에서 중요한 역할을 하는 노드를 집합적으로 계산하여 제거.

    그래프 해체 기계 학습(Graph Dismantling with Machine Learning, GDM): 기계 학습을 이용하여 네트워크 내 취약한 노드를 분류하고, 이를 기반으로 네트워크를 해체.

4-2. Results

  • 실험 결과, 제안된 GNN 및 강화학습 기반 방법론은 기존의 전통적 방법들에 비해 전반적으로 우수한 성능을 보였으며, 각 네트워크에서의 성능은 아래와 같음.

    전력망 성능: 제안된 방법론은 10,887개의 노드 중 10개 이하의 노드를 손상시켰을 때, 전력량을 약 50% 감소시킴. 이는 CI 방법에 비해 약 50% 더 낮은 전력량을 보여주며, 전력망의 취약 노드 식별에 있어서 높은 성능을 보임.

    도로망 성능: 제안된 방법론은 주요 도로망의 연결성을 약 75%, 부차적 도로망에서는 약 43% 감소시키며, 다른 방법들보다 더욱 효율적으로 취약 노드를 식별.

Figure 4. Performance of different methods on different networks - 전력망 및 도로망에서 제안된 방법론과 기존 방법론의 성능 비교.

  • 도시 인프라 네트워크는 시간이 지남에 따라 변동할 가능성이 상존하여, 새로운 네트워크 환경에 대한 모델의 적응력을 평가하는 것이 중요함. 이에 본 연구에서는 제안된 모델의 전이 가능성을 평가하였으며, 새로운 네트워크 토폴로지에서도 제안된 방법론은 기존 방법론 대비 우수한 성능을 보임.

    전력망 성능: 새로운 전력망 환경에서, 제안된 방법론은 CI 방법 대비 전력량을 약 46% 더 많이 감소.

    결합 네트워크 성능: 결합 네트워크에서 제안된 방법론은 CI에 비해 약 3.4배 높은 보상을 획득.

Figure 5. Transferring ability for different Networks - 새로운 네트워크 토폴로지에서의 전력망 및 결합 네트워크 성능 비교.

  • 제안된 방법론의 각 구성 요소가 성능에 미치는 영향을 평가하기 위해, GNN을 통한 노드 임베딩과 강화학습 기반 최적화가 취약 노드 식별에 얼마나 효과적인지 검증. GNN을 사용하여 사전 학습된 임베딩을 적용한 경우, 랜덤 임베딩을 적용한 경우보다 우수한 성능을 보였으며, 복잡한 상호 의존적 네트워크에서 GNN 임베딩을 사용한 강화학습은 특히 안정적인 성능을 보임.

Figure 6. Ablation experiments for different networks - GNN을 이용한 사전 학습 임베딩과 랜덤 임베딩을 사용한 경우의 성능 비교.

Figure 7. Process of finding vulnerable nodes in interdependent network - 상호 의존적 도시 인프라 네트워크에서 취약 노드를 탐색하는 과정. (전력망의 경우 직접적 손상을 green, 간접적 손상을 yellow로 표현 하였으며, 도로망의 경우 직접적 도로 손상을 light green, 발전소 손상에 의한 도로망 영향범위를 magenta, 일련의 손상으로 인해 주요 도로망과 단절된 도로를 red로 표현)

5. Conclusion

  • 본 연구는 도시 인프라 네트워크의 취약성을 분석하기 위해 그래프 신경망(GNN)과 강화학습(RL)을 결합한 새로운 데이터 기반 방법론을 제안하고 있음. 전력망과 도로망 같은 상호 의존적 네트워크에서 취약한 노드를 효과적으로 식별하고, 그 노드가 네트워크 전체에 미치는 연쇄적 손상을 예측하는 데 있어 제안된 방법론은 기존의 전통적인 접근법보다 우수한 성능을 보임.

    모델 특성: 제안된 GNN 기반 모델은 네트워크 구조의 복잡한 상호작용을 효율적으로 학습하며, 취약한 노드를 정확하게 예측 함. 특히, 강화학습을 통해 네트워크 손상 시의 영향을 보상 함수로 정의하고, 이를 통해 최적의 취약 노드 선택 정책을 학습함으로써, 전통적인 차수 기반 또는 집합 영향력(CI) 기반 방법론보다 뛰어난 성능을 발휘하였다.

    모델 전이 가능성: 제안된 모델은 전이 가능성 평가에서도 우수한 성능을 보였으며, 새로운 네트워크 토폴로지에 적응할 수 있음을 입증함. 이는 도시 인프라 네트워크가 시간이 지나면서 그 구조와 상호 관계가 변할 때도, 본 연구의 방법론이 유연하게 적용될 수 있음을 시사함.

  • 본 연구는 상호 의존적 네트워크에서의 취약 노드 파악 등 분명한 개선점을 시사하나, “그래프 기계학습”의 연구 측면에서 아래와 같은 한계점 및 추후 연구방향을 함께 내포하고 있음.

    그래프 모델링에서의 단순화: 제안된 모델은 전력망과 도로망의 상호작용을 네트워크 노드와 엣지로 표현하며, 상호의존성을 단순화하여 모델링 하고 있음. 그러나 실제 시스템은 훨씬 복잡한 물리적, 운영적, 그리고 시간적 동역학을 포함하며 (전력망의 부하 분산, 도로망의 교통량 변화), 이러한 메커니즘의 반영을 통해 더욱 실효성 있는 결과를 생산할 수 있을 것.

    연쇄적 손상 (Cascade Failure) 메커니즘의 제한: 본 연구에서는 임의의 손상을 부여하여 네트워크의 취약성을 파악. 실제 Cascade Failure는 Gradual Failure (소규모 결함이 시간이 지나면서 큰 영향), Simultaneous Failure (여러 노드가 동시에 손상되어 광범위한 영향) 등 다양한 유형의 기작이 있는 만큼, 이를 상황별로 부여 및 모사할 수 있는 모델의 개발이 추후 과제가 될 수 있음.

    다중 인프라 네트워크 통합: 본 연구는 도로망과 전력망이라는 두 네트워크의 결합에 집중 하였으나, 실제 도시 인프라 시스템은 통신/수도/대중교통 등 여러 네트워크가 상호작용. 제안된 모델은 다양한 네트워크를 추가로 반영할 수 있는 역량을 갖추고 있는 것으로 판단되는바, 추후 이에 대한 고려를 통해 더욱 사실적인 모델을 구현 할 수 있을 것으로 기대됨.

Author Information

  • Hongtak Lee Ph.D Candidate, Moon Soul Graduate School of Future Strategy

References

  1. Chiara, G., Conrad, D. (2019). UK power cuts: Almost a million customers left without electricity as massive National Grid failure causes travel chaos. https://www.independent.co.uk/travel power-cuts-london-south-east-traffic-lights-trains-transport-down-latest-updates-a9050596.html. Independent.
  2. Prakash, J., Murali, L., Manikandan, N., Nagaprasad, N., & Ramaswamy, K. (2024). A vehicular network based intelligent transport system for smart cities using machine learning algorithms. Scientific reports, 14.
  3. Li, Z., Chen, Q., & Koltun, V. (2018). Combinatorial optimization with graph convolutional networks and guided tree search. Advances in neural information processing systems, 31.
  4. Morone, F., & Makse, H. A. (2015). Influence maximization in complex networks through optimal percolation. Nature, 524(7563), 65-68.
  5. Iyer, S., Killingback, T., Sundaram, B., & Wang, Z. (2013). Attack robustness and centrality of complex networks. _PloS one, 8(4), e59613.
  6. Cohen, R., Erez, K., Ben-Avraham, D., & Havlin, S. (2000). Resilience of the internet to random breakdowns. Physical review letters, 85(21), 4626.
  7. Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E., & Havlin, S. (2010). Catastrophic cascade of failures in interdependent networks. Nature, 464(7291), 1025-1028.