1. Problem Definition

개인화 추천시스템 분야에서 대표적인 방법론인 협력 필터링 (Collaborative Filtering) 에서 유저와 아이템의 표현(Representation) 방식을 개선하기 위한 다양한 시도가 이루어지고 있습니다. 특히, 기존의 고전적인 방법론보다 더 풍부하고 협력 필터링에 유의미한 신호를 반영하기 위해, 유저와 아이템의 상호작용 데이터를 그래프로 변환하고, 이를 기반으로 그래프 신경망(Graph Neural Networks) 을 적용하는 연구가 주목받고 있습니다.

이러한 접근법은 기존 방식보다 향상된 유저와 아이템의 표현(벡터)을 생성하는 데 성공하였으며, 이를 활용한 추천시스템의 성능은 크게 개선되었습니다. 이러한 그래프 신경망 기반의 협력 필터링 방법은 일반적으로 Graph-based Collaborative Filtering (GCF) 라고 불립니다.

그러나 GCF의 뛰어난 성능에도 불구하고, 표현 인코딩에 사용되는 상호작용 데이터와 관련된 두 가지 주요 문제점이 존재하여 성능에 제약을 초래하고 있습니다.

1. Popularity bias

사람마다 특정 플랫폼에서 구매하거나 상호작용하는 물품의 수가 다르듯이, 모든 유저와 아이템이 동일한 수의 상호작용 (interaction) 을 가지지는 않습니다. 일반적으로 추천시스템에 사용되는 데이터는 Long-tail 분포를 특징으로 하며, 이는 전체 유저와 아이템 중 일부에 상호작용이 집중되는 경향을 보입니다. 이러한 데이터 분포를 그래프로 변환하고 GCF 인코더에서 표현을 생성할 때, 만들어진 표현(벡터)은 잠재 벡터 공간 (Latent Space) 내에서 인기 있는 유저와 아이템의 표현 벡터 근처로 분포가 집중되는 편향이 발생할 수 있습니다.

이로 인해, 코사인 유사도 점수를 기반으로 추천을 수행하는 시스템은 인기 있는 아이템을 더 자주 추천하고, 상대적으로 덜 인기 있는 아이템은 추천하지 않는 인기 편향(Popularity Bias) 문제가 나타납니다. 이는 다양한 아이템을 추천해야 하는 시스템의 목적에 부합하지 않으며, 추천 품질 저하로 이어질 수 있습니다.

2. Noisy in interactions

추천시스템에서는 유저의 명확한 성향을 반영하는 명시적 상호작용(explicit interaction) 데이터를 확보하기가 매우 어렵습니다. 이에 따라, 일반적으로 클릭 여부와 같은 암묵적 상호작용(implicit interaction) 데이터를 활용합니다. 그러나 이러한 데이터에는 랜덤 클릭이나 실수로 인한 클릭과 같은 노이즈 상호작용(noisy interaction) 이 포함될 수 있으며, 이는 유저의 실제 선호를 제대로 반영하지 못합니다.

이러한 노이즈 상호작용이 포함된 데이터를 기반으로 GNN을 사용하는 GCF 모델이 유저와 아이템의 표현을 생성할 경우, 노이즈 정보가 표현에 반영될 위험이 있습니다. 이는 추천 성능에 심각한 악영향을 미치며, 추천 품질을 크게 저하시킬 수 있습니다.

이러한 GCF의 치명적인 문제를 완화하기 위한 방법으로 대조학습(Contrastive Learning, CL) 을 GCF에 적용하려는 시도가 이루어지고 있습니다. 대조학습은 자기지도 학습(Self-supervised Learning) 의 대표적인 방법 중 하나로, 데이터 증강을 활용하여 인코더가 노이즈에 강인한 표현 벡터를 생성하도록 돕습니다.

또한, 대조학습은 인코더가 증강된 데이터와 원본 데이터에서 공유되는 핵심 특성을 반영한 표현 벡터를 생성하도록 유도하여, 모델이 보다 일반화된 표현을 학습할 수 있도록 기여합니다.

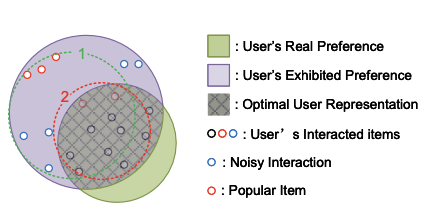
Problems of random_dropout

GCF 분야에서 대조학습을 위해 사용하는 대표적인 데이터 증강 방식은, 사용자(user) 또는 아이템(item) 중 일부의 기존 상호작용 데이터를 랜덤하게 제거하거나, 유저 및 아이템을 데이터에서 제거하고 변형된 상호작용 데이터를 기반으로 새로운 그래프 데이터를 생성하는 방법입니다. 이렇게 생성된 증강 데이터는 변형 이전의 데이터와 함께 그래프 신경망(GNN) 을 활용하여 유저와 아이템의 표현 벡터를 생성하는 데 사용되며, 생성된 표현 벡터는 대조학습의 학습 과정에 활용됩니다.

그러나 이 방식에는 중요한 문제가 하나 있습니다.

GCF는 유저와 아이템의 표현 벡터를 생성할 때, 이 둘 간의 상호작용을 엣지(edge) 로 나타낸 그래프 데이터를 활용합니다. 여기서 유저 벡터를 예로 들면, 최적의 유저 표현 벡터를 생성하려면, 유저가 실제로 선호하는 아이템들(2번 동그라미 안에 있는 아이템들)만이 해당 유저와 엣지로 연결되어 있어야 합니다.

하지만 일반적으로 사용되는 상호작용 데이터에는 노이즈 상호작용(noisy interaction) 이 포함되어 있으며, 이는 유저를 기준으로 보라색 동그라미 안에 포함된 아이템들처럼 유저의 실제 선호를 반영하지 않는 데이터를 포함하게 됩니다. 이러한 노이즈 상호작용은 유저 표현 벡터의 품질을 저하시킬 수 있는 주요 원인이 됩니다.

대조학습에서 데이터 증강으로부터 생성된 표현 벡터가 가장 의미 있게 활용되기 위해서는, 모든 유저와 아이템에 대해 2번 동그라미 안의 아이템(유저) 과의 상호작용만을 남기고, 나머지 아이템(유저)과의 상호작용을 제거한 변형 상호작용 데이터를 기반으로 그래프를 생성해 GNN에 활용해야 합니다. 그러나 랜덤한 방식으로 상호작용을 제거하면, 주어진 유저 및 아이템에 대해 일반적으로 1번 동그라미 형태의 상호작용이 남게 됩니다.

또한, 기존 논문에서는 GCF에 대조학습을 적용하는 방식에도 한계점을 지적합니다. 일반적으로 GCF에서 대조학습은 상호작용 데이터를 변형하여 두 가지 다른 그래프를 생성한 뒤, 각 그래프를 동일한 GNN 인코더를 통해 처리해 생성된 표현 벡터가 같은 노드(유저 및 아이템)에 대해 동일한 표현 벡터로 수렴하도록 학습하는 목적함수를 설정해 모델을 학습시킵니다.

하지만 앞서 언급했듯이 증강된 데이터가 불필요한 상호작용을 다수 포함하고 있을 경우, 이러한 데이터를 기반으로 생성된 두 표현 벡터를 대조하여 동일한 표현 벡터를 만들도록 학습하는 과정은 GNN을 사용하는 데이터 인코더의 학습을 저해할 수 있습니다. 이는 모델 성능을 저하시키는 주요 원인 중 하나로 작용할 수 있습니다.

2. Motivation

논문에서는 위에서 언급한 문제들에 대한 해결 방안으로 머신러닝 기반의 학습 가능한 데이터 증강 방식과 새로운 GCF 대조학습 프레임워크를 제시합니다.

1. 학습가능한 데이터(그래프) 방식

논문에서는 MLP 기반의 학습 가능한 증강 방식을 통해, 상호작용 그래프 내에서 특정 상호작용 또는 노드를 선정해 제거하는 방법을 제안합니다. 이 데이터 증강 함수는 인기 노드의 영향을 줄이고, 비인기 노드의 정보를 보호하는 방향으로 학습되어, 대조학습에 사용할 증강 그래프를 생성합니다. 이를 통해 인기 편향(popularity bias) 을 예방할 수 있다고 주장합니다.

2. 증강데이터와 기존 데이터의 결합

기존의 GCF 대조학습 방식은 증강 함수를 통해 생성된 그래프를 인코더에 통과시켜 얻은 표현 벡터를 대조하는 방식으로 작동합니다. 그러나 논문에서는 각 증강 데이터의 표현과 원래 상호작용 그래프(original interaction graph) 에서 생성된 표현을 통합하는 multi-view representation 아이디어를 제안합니다. 이 접근법은 각 증강 데이터가 가진 정보를 통합함으로써 모델의 견고성을 강화하는 데 기여할 수 있다고 주장합니다.

이 과정에서 중요한 점은, 각 증강 데이터로부터 생성된 표현이 추천 시스템의 본래 목적에 효과적인 표현이어야 하며, 통합된 표현이 최대 효과를 발휘하려면 각 표현이 서로 다른 유용한 정보를 포함해야 한다는 것입니다. 이를 실현하기 위해 논문에서는 정보이론(Information Theory) 의 개념을 활용합니다.

정보 병목(Information Bottleneck, IB) 개념의 적용

논문에서는 Information Bottleneck (IB) 개념을 적용하여, 증강 데이터와 원래 데이터 사이의 상호 정보(mutual information) 를 최소화하면서도, 추천 성능에 효과적인 표현을 생성할 수 있는 증강 데이터를 만들어냅니다. 이를 통해, 각 데이터 표현이 추천 시스템의 성능을 높이는 데 유의미한 정보를 담을 수 있도록 보장합니다.

3. Method

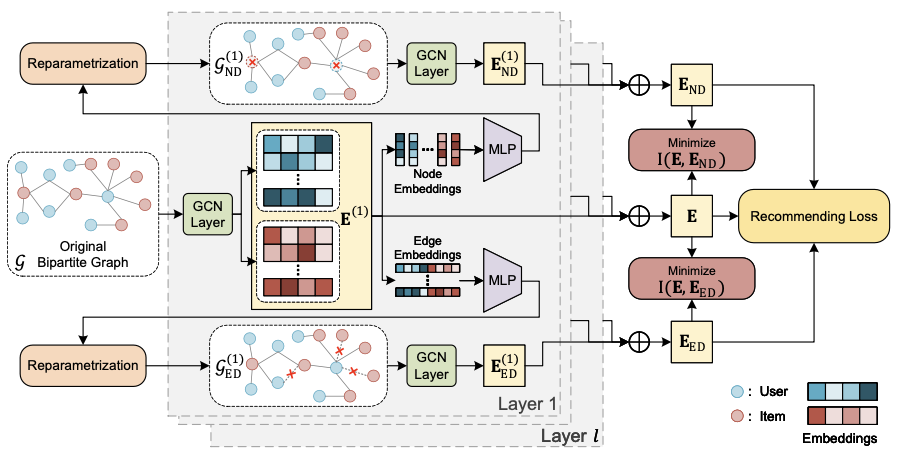
Framework of CGI

3.1 Preliminary

  1. 데이터
    $U \text{(user set)} = {u_{1}, u_2, u_3, …. , u_m}$
    $I \text{(item set)} = {i_{1}, i_2, i_3, …. , i_n}$
    $R \text{(relation matrix)} \in \mathbb{R}^{m*n}$
    $(r_{u,i} = 1\text{ if there’s an interaction between user } u \text{ and item }i \text{ else 0})$

  2. GNN encoder의 동작방식 (LightGCN) GNN 기반 데이터 인코딩을 수행하기 위해, 주어진 데이터를 그래프 $G=(V,E)$로 변환합니다.

    $V = U \cup I \text{ and } E\text{(edge)} = {e_ {u,i} \vert r_ {u,i} = 1, u \in U, i \in I}$

    여기서 $U$는 유저 집합, $I$는 아이템 집합이며, $r_{u,i}$는 유저 $u$와 아이템 $i$ 간의 상호작용 여부를 나타냅니다. 주어진 $R$ 로 부터 인접행렬(Adjacency Matrix) 을 만들어 사용합니다.

    $A =\begin{bmatrix} 0 & R \ R^T & 0 \end{bmatrix}$

    추천시스템에서 GNN 인코더는 일반적인 GCN 인코더와 유사하게, 정해진 GCN 레이어 수만큼 이웃 노드의 표현 정보를 수집하여 최종 노드 표현을 생성합니다. 이 과정을 수식으로 나타내면 다음과 같습니다: $\mathbf{E}^{(l)} = GCN(\mathbf{E}^{(l-1)}, G)$

    이때, 초기 노드의 표현 ($\mathbf{E}^{(0)}$) 는 모델이 학습 가능한 파라미터로 설정됩니다.

    행렬 연산 관점이 아닌 노드 표현 관점에서 이 과정을 재정리하면 다음과 같이 표현할 수 있습니다:

    $e_ {u}^{(l)} = f_ {combine}(e_ {u}^{(l-1)}, f_ {aggregate}^{l}({e_ {i}^{(l-1)} \vert i \in N(u)}))$

    여기서:

    • $N(u)$ : 유저 ( u )의 이웃 노드 집합
    • $f_{\text{aggregate}}$ : 이웃 노드로부터 정보를 집계(aggregation)하는 함수
    • $f_{\text{combine}}$: 집계된 정보를 기존 노드 표현과 결합(combine)하는 함수

    이 과정을 $L$ 번 반복하며, 각 레이어에서 생성된 표현을 저장한 후, $f_{\text{readout}}$ 함수로 최종 표현 $e$를 계산합니다:

    $e = f_ {readout}({e^{l} \vert l = 0,1,2,…L})$

    LightGCN의 경우, 집계(aggregation)는 단순히 이웃 노드의 표현을 선형 결합하는 방식으로 이루어집니다. 이러한 과정을 $L$ 번 반복하며 각 레이어에서 생성된 표현을 $f_{\text{readout}}$을 통해 통합하여 최종 표현을 생성합니다. $f_{\text{readout}}$은 단순히 평균이나 각 레이어 표현의 합을 사용하는 방식으로 구현됩니다. LightGCN의 레이어별 표현은 주어진 행렬 데이터를 기반으로 다음과 같이 계산됩니다:

    $\mathbf{E}^{(l)} = (D^{-0.5}\tilde{A}D^{-0.5}\mathbf{E}^{(l-1)})$

    여기서:

    • $D$ : 그래프 ( A )의 degree matrix (대각 행렬)
    • $\tilde{A}$ : 정규화된 인접 행렬

    LightGCN은 유저와 아이템의 표현을 통해 내적 $r_{ui}​=e_{u}^{T}e_{i}$​을 사용하여 유저의 선호 점수를 예측합니다. 이는 대부분의 추천 시스템에서 널리 사용되는 방식입니다. LightGCN은 Bayesian Personalized Ranking (BPR) 손실 함수 $\mathcal{L}_{rec}$​을 사용하여 모델 파라미터를 최적화합니다:

    $\mathcal{L}_ {rec}=\sum_ {(u,i,j) \in \mathcal{O}} -\ln \sigma(\hat{r}_ { ui} - \hat{r}_ {uj})$

    여기서:

    • $\mathcal{O} = {(u, i, j) \mid (u, i) \in \mathcal{R}^+, (u, j) \in \mathcal{R}^-}$: pairwise 학습 데이터, $\mathcal{R}^{+}$ 는 관찰된 상호작용을 나타내고, $\mathcal{R}^{-}$ 는 관찰되지 않은 상호작용을 나타냅니다.
    • $\sigma$ 는 sigmoid 함수

    이 논문에서도 추천 작업을 위한 목적 함수로 BPR 손실을 사용합니다.

    3.2 Main Method

    이 논문에서는 앞서 설명한 LightGCN 인코더를 활용하여, 제안된 증강 함수를 통해 생성된 각각의 증강 그래프와 원래 데이터 그래프의 표현을 생성하고, 이를 결합하여 최종 표현을 만들어냅니다. 아래에서는 논문의 핵심인 각 증강 함수에 대해 설명합니다.

3.2.1 Learnable Node-Dropping

기존의 단순히 랜덤하게 그래프 노드를 제거하는 방식과 달리, 이 논문에서는 학습 가능한 노드 제거 방식을 제안합니다. 이는 다음과 같이 공식화됩니다:

$G_ {ND}^{l} = ({(v_ {i} \odot p_ {i}^{l} \vert v_ {i} \in V }, E)$

여기서:

  • $p_ {i}^{l} \in {0,1}$은 학습 가능한 파라미터 $w_ {i}^{l}$에 의해 확률적으로 결정되며, 이는 베르누이 분포를 따릅니다.

이렇게 레이어별로 일부 노드가 제거된 그래프를 GCN 인코더에 적용하여 각 레이어별 새로운 표현을 생성합니다. 이 과정은 다음과 같이 표현됩니다:

$\mathbf{E}^{(l)}_ {ND} = GCN(\mathbf{E}_ {ND}^{(l-1)}, G_ {ND}^{l})$

3.2.2 Learnable Edge-Dropping

Node-Dropping과 유사하게, 엣지(Edge) 역시 학습 가능한 방식으로 일부 제거하여 새로운 그래프를 생성합니다. 이 과정은 다음과 같이 공식화됩니다:

$G_ {ED}^{l} = (V, {(e_ {ij} \odot p_ {ij}^{l} \vert e_ {ij} \in E })$

여기서:

  • $p_{ij}^{l} \in {0,1}$은 학습 가능한 파라미터 $w_{ij}^{l}$에 의해 확률적으로 결정되며, 이는 베르누이 분포를 따릅니다.

이와 같은 방식으로 레이어별로 일부 엣지가 제거된 그래프를 GCN 인코더에 적용하여 각 레이어별 새로운 표현을 생성합니다. 이 과정은 다음과 같이 표현됩니다:

$\mathbf{E}^{(l)}_ {ED} = GCN(\mathbf{E}_ {ED}^{(l-1)}, G_ {ED}^{l})$

3.2.3 $w_{i}^{l}, w_{ij}^{l}$ 계산

각 노드 및 엣지를 제거할 확률 $w_{i}^{l}$ 와 $w_{ij}^{l}$는 다음과 같이 $l$ 번째 레이어에서 노드 및 엣지를 구성하는 노드 표현 $(e_{i}^{l}, e_{j}^{l})$ 을 다층 신경망(Multi-Layer Perceptron, MLP)에 통과시켜 계산합니다:

$w_{i}^{l} = MLP(e_{i}^{l}), w_{ij}^{l} = MLP(e_{i}^{l}, e_{j}^{l})$

3.2.4 Information Bottleneck에 기반한 Training

이 논문에서는 기존 대조학습에서 사용하던 방식과는 차별화된 새로운 목적함수를 제시합니다. 이 목적함수는 정보이론의 Information Bottleneck (IB) 개념을 기반으로 하며, 증강 데이터로 생성된 표현과 기존 데이터로 생성된 표현 간의 분산을 증가시키는 동시에, 각각의 증강 데이터 표현이 추천 목적에 맞도록 학습 방향을 조정합니다. 이를 수식으로 나타내면 다음과 같습니다:

$\min_ {E;\tilde{E}}\tilde{\mathcal{L}}_ {Rec} + I(E;\tilde{E})$

$I(E;\tilde{E})=I(E_ {u};\tilde{E_ {u}})+I(E_ {i};\tilde{E}_ {i})$ 여기서 :

  • $I(E; \tilde{E})$ : 증강 데이터 표현 $( \tilde{E})$과 기존 데이터 표현 $( E)$ 간의 상호 정보(Mutual Information) 양
  • $I(E; \tilde{E}) = I(E_ {u}; \tilde{E}_ {u}) + I(E_ {i}; \tilde{E}_ {i})$ : 유저와 아이템 표현 각각에 대한 상호 정보의 합
  • $\tilde{E}$ : $E_{ND}$와 $E_{ED}$를 대신하는 증강 데이터 표현
  • $\tilde{\mathcal{L}}_ {rec}$ : $E_ {ND}$와 $E_ {ED}$로부터 생성된 표현을 활용한 BPR 손실 함수

위 목적함수를 최적화하려면 $I(E; \tilde{E})$를 계산해야 합니다. 상호 정보는 계산이 복잡하므로, 일반적으로 InfoNCE 손실 함수를 사용하여 이를 근사합니다. InfoNCE 손실 함수의 최소화는 상호 정보의 하한값을 최대화하는 역할을 하며, 반대로 Negative InfoNCE 손실 함수를 최소화하면 상호 정보의 상한값을 최소화시키는 방향으로 작동합니다. 이를 활용하여 목적함수를 재구성합니다:

$I(E_ {u};\tilde{E}_ {u}) = -{\sum_ {u \in U} \log \frac{\exp(\text{sim}(\mathrm{e}_ {i}, \tilde{\mathrm{e}_ {i}}) / \tau)}{\sum_ {j\in U} \exp(\text{sim}(\mathrm{e}_ {i}, \tilde{\mathrm{e}}_ {j}) / \tau)}}$

여기서 :

  • $\text{sim}$ 은 Cosine similarity
  • $\tau$= temperature (하이퍼파라미터))

위 수식은 추천 시스템의 목적함수와 함께 멀티태스크 최적화에 활용됩니다. 최종 목적함수는 다음과 같이 정의됩니다:

$\mathcal{L} = \mathcal{L}_ {rec} +\mathcal{L}_ {rec}^{ND}+\mathcal{L}_ {rec}^{ED} + \lambda(I(E;\tilde{E}_ {ND})+I(E;\tilde{E}_ {ED})) + \beta \vert\vert \theta \vert\vert^{2}_ {2}$

여기서 :

  • $\mathcal{L}_ {\text{rec}}$: 추천 손실 함수(BPR 손실 함수)
  • $\mathcal{L}_ {\text{rec}}^{ND}, \mathcal{L}_ {\text{rec}}^{ED}$: 각각 Node-Dropping과 Edge-Dropping에서의 추천 손실 함수 ($\tilde{\mathcal{L}}_ {rec}$)
  • $\lambda$: 상호 정보 손실을 조정하는 가중치
  • $\beta$ : 정규화(L2 정규화) 항의 가중치
  • $||\theta||_{2}^{2}$ : 모델 파라미터에 대한 L2 정규화

    4. Experiment

    1. 실험데이터: Yelp2018, MovieLens-1M, Douban (Training:Validation:Test = 8:1:1)
    2. 평가지표(랭킹기반 지표): Recall@10, 20 / NDCG(Normalized Discounted Cumulative Gain)@10, 20
    3. 비교 Baseline 모델: BPRMF, NCF, NGCF, LightGCN, DNN+SSL, SGL Matrix Factorization 기반: BPRMF, NCF 그래프 기반 협력 필터링 기반: NGCF, LightGCN 대조학습 기반 : DNN + SSL, SGL
    4. 논문 메소드 하이퍼파라미터 세팅: 초기 유저 및 아이템 파라미터는 랜덤값으로 설정. (차원은 둘다 64차원으로 고정) / 최적화 방식은 Adam optimizer 채택. / Batch size는 2048로 설정. / 목적함수의 정규화 term의 weight는 $\lambda = 0.02, \beta =0.01$ 로 설정.

4.1 실험결과(Baseline과 추천 관련 벤치마크 비교)

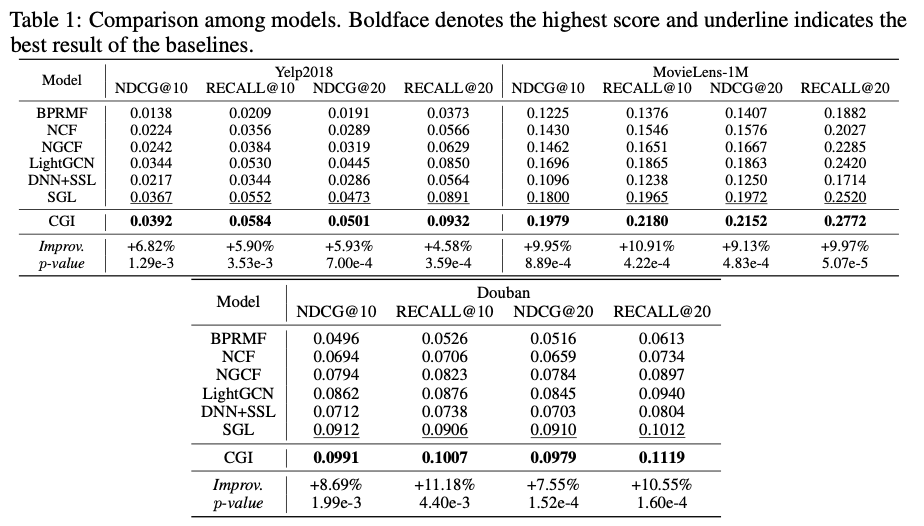
Baseline Comparement

결론적으로, CGI(논문 메소드) 는 세 가지 실험 데이터셋에서 모든 베이스라인의 성능 지표를 압도적으로 능가했습니다. 특히, 두 번째로 높은 성능을 보인 SGL보다 Yelp 데이터에서는 약 5.9%, MovieLens-1M 데이터에서는 약 10%, Douban 데이터에서는 약 10% 성능이 개선되었습니다.

전반적인 결과를 분석해 보면, 초기 추천 시스템에서 주로 사용되었던 Matrix Factorization (MF) 기반 모델보다 그래프 기반 협력 필터링(GCF) 모델의 성능이 더 우수함을 확인할 수 있습니다. 이는 그래프 기반 추천 모델이 GNN을 통해 다양한 이웃 아이템과 유저의 정보를 활용하여 유저 및 아이템을 대표하는 벡터를 생성할 수 있기 때문입니다. 단순히 유저-아이템 상호작용 행렬을 분해하여 벡터를 생성하는 MF 모델보다, 이 방식은 더 높은 추천 성능을 내는 벡터를 만들어냅니다.

또한, 대조학습을 MF 모델에 적용한 DNN+SSL 모델보다 그래프 기반 모델인 SGL과 CGI의 성능이 뛰어난 점은 이 주장을 더욱 강화해줍니다. 특히, 그래프 기반 모델에 대조학습을 적용했을 때의 성능 향상은, 대조학습이 그래프 기반 모델에 내재된 문제를 완화할 수 있음을 시사합니다.

SGL 모델과 CGI의 비교는 이 논문의 핵심 주장과 맞닿아 있습니다. 대조학습을 적용하는 과정에서, SGL처럼 랜덤하게 그래프를 변형하여 증강 데이터를 생성하는 것보다, CGI처럼 정보 이론에 기반한 학습된 모듈을 통해 최적화된 증강 데이터를 사용하고 각 그래프 표현을 통합하는 multi-view representation 방법이 그래프 기반 협력 필터링에서 더 큰 효과를 발휘함을 보여줍니다.

4.2 실험결과(보충실험)

  1. Random Dropout 증강방식과의 비교 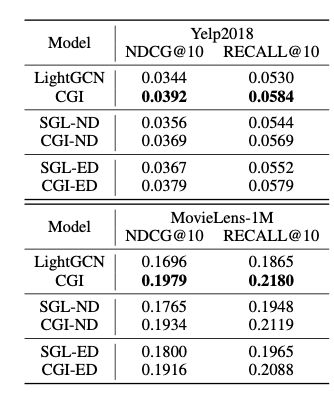Ablation_study_1 직전 실험에서는 CGI 메소드가 SGL의 랜덤한 그래프 변형을 통한 증강 데이터 표현에 대조학습을 적용했을 때보다 그래프 추천 시스템의 성능을 더 크게 개선하는 결과를 보였습니다. 이 보충 실험은 위 결과와 더불어 그래프 기반 협력 필터링에서 증강 데이터를 활용하는 효과를 보다 상세히 보여줍니다.

해당 실험에서는 동일한 데이터 증강 방식(Node Dropout, Edge Dropout)을 적용했을 때, 이를 랜덤한 증강 함수로 수행하여 대조학습에 사용하는 SGL과 학습된 모듈이 생성한 증강 그래프를 최종 표현 생성에 사용하는 CGI 두 모델의 성능을 비교했습니다. 기본적으로 두 모델 모두 어떤 방식의 데이터 증강을 사용하든 그래프 기반 협력 필터링의 대표 모델인 LightGCN보다 성능이 우수함을 확인할 수 있습니다. 같은 증강 방식에서 두 모델을 비교할 경우, 언제나 CGI 모델이 더 높은 성능을 보였습니다.

더 깊이 있는 분석을 통해, 하나의 증강 방식만을 사용한 CGI-ED (Edge Dropout 사용)와 CGI-ND (Node Dropout 사용) 모델보다 두 증강 방식을 모두 사용한 CGI 모델이 더 우수한 성능을 보임을 확인할 수 있습니다. 이는 두 가지 증강 방식이 각각 다른 관점에서 유의미한 시그널을 생성하며, 두 방식을 모두 사용할 때 하나만 사용할 때보다 추천 시스템에 더 유용한 유저 및 아이템 벡터를 생성하는 데 시너지를 제공함을 시사합니다.

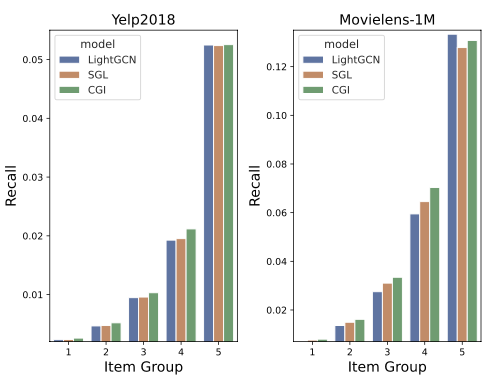  1. GCF 문제 개선 ablation_study_2 앞서 문제 정의에서 그래프 기반 협력 필터링(GCF)에 인기 편향이라는 큰 문제가 존재함을 언급했습니다. 이번 실험에서는 CGI가 실제로 인기 편향을 완화하는 데 기여하는 메소드임을 보여줍니다. 먼저, 아이템을 상호작용 수에 따라 5개의 그룹으로 나누었습니다. (그룹 번호가 클수록 상호작용이 많은 아이템 집합을 의미) 각 그룹에 속하는 아이템이 유저에게 어느 정도로 추천되는지를 실험을 통해 확인하고자 했습니다.

이 실험 결과는 추천 시스템이 인기가 많은 아이템을 더 자주 추천하는 경향이 있음을 보여주며, 이로 인해 덜 인기 있는 아이템은 발견될 가능성이 낮아져 Long-tail 분포가 더욱 심화됩니다. 또한, CGI는 Long-tail 아이템에 대한 추천 정확도를 크게 향상시키는 데 기여할 수 있음을 확인할 수 있었습니다.

비록 CGI와 SGL 모두 상위 20%의 인기 아이템에서는 큰 우위를 보이지 않지만, 전반적인 성능 개선을 통해 이들이 유저의 선호 표현에서 롱테일 아이템의 정보를 더 잘 포착할 수 있음을 알 수 있습니다. 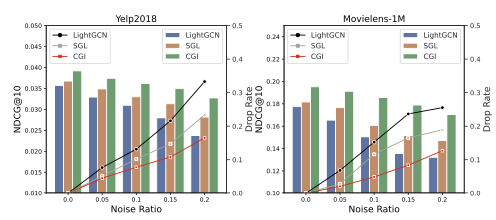ablation_study_3 데이터의 노이즈에 취약한 GCF의 문제를 완화하는 CGI의 효과 또한 실험을 통해 확인할 수 있습니다. 이 실험은 원래 데이터에 노이즈 상호작용을 전체 상호작용의 0~20%까지 추가했을 때 모델의 성능 변화를 나타내는 그래프입니다. 노이즈가 증가함에 따라 비교 모델과 CGI 모두 성능이 감소하는 것을 확인할 수 있습니다. 그러나 CGI의 경우 다른 모델에 비해 성능 감소 폭이 현저히 줄어들었으며, 계속해서 가장 우수한 추천 성능을 유지하는 것을 알 수 있습니다. 이는 CGI 프레임워크가 상호작용 데이터의 노이즈를 더 효과적으로 완화할 수 있음을 시사합니다.

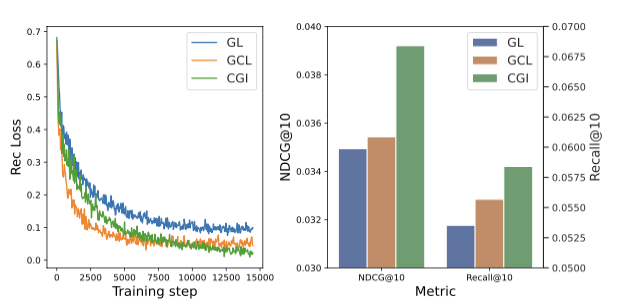  1. Information Bottleneck의 효과 ablation_study_4 Information Bottleneck의 효과 역시 논문에서는 실험을 통해 검증하고자 했습니다. 이 실험에서는 $I(E;\tilde{E})$를 증강 함수의 학습에 사용되는 목적 함수에서 제거한 모델(GL)과, 목적 함수를 $\min_ {E;\tilde{E}}\tilde{\mathcal{L}}_ {Rec} -I(E;\tilde{E})$ 로 변형하여 원래 데이터와 변형 데이터의 상호 정보량을 극대화하는 방향으로 학습한 모델(GSL), 그리고 CGI의 성능을 비교했습니다. Yelp 데이터를 사용하여 모델의 훈련 과정에서 수렴 속도와 성능을 측정했습니다. 결과적으로, $I(E;\tilde{E})$가 목적 함수에 포함된 경우가 포함되지 않은 경우보다 훨씬 빠르게 수렴하는 것을 확인할 수 있었습니다. 또한, 성능 면에서도 CGI가 다른 두 모델을 압도하는 결과를 보였습니다. 논문에서는 이러한 결과를 통해 추천에 무관한 노이즈 정보를 제거하는 데 정보이론에 기반해 설계한 목적함수가 도움이 되었기 때문이라 주장합니다.

Result(Discussion)

이 논문은 학습 가능한 그래프 증강 방식을 도입하여, 그래프 협력 필터링에 도움을 줄 수 있는 데이터 증강 과정에서 핵심 상호작용(core-interaction) 이 손실되는 것을 방지할 수 있었습니다.

다만, 논문의 MLP 기반 증강방식은 모델의 파라미터 복잡도를 증가시킵니다. 또한 추천 시스템의 암묵적 상호작용(implicit interaction) 에서 노이즈를 명확히 정의하기 어려운 한계가 있기 때문에 드롭아웃 비율($w_{i}, w_{ij}$)이 충분히 잘 학습 되더라도 여전히 핵심 상호작용이 제거될 위험이 존재합니다. (주어진 데이터로 증강함수를 학습하는 것 자체가 문제가 될 수 있다고 생각합니다.)

그럼에도 불구하고, 이 논문은 증강 데이터에 포함된 노이즈를 머신러닝 기반 방법론으로 줄일 수 있다는 인사이트를 제공하며, Multi-view representation과 Information Bottleneck이라는 아이디어는 앞으로도 GCF 도메인에서 증강을 활용한 인코딩 방식에 자주 활용될 수 있을 것으로 보입니다. 이러한 점에서 매우 유용한 인사이트를 제공한 논문이라고 생각합니다.

Source Code(Materials)

https://github.com/weicy15/CGI