[NeurIPS - 23] Adversarial Robustness in Graph Neural Networks: A Hamiltonian Approach
Introduction
-
GNN은 social media, molecular, chemistry, mobility 등 네트워크 형태의 데이터에 적용 시 뛰어난 추론 능력을 보이나, adversarial attack에 취약하다는 약점이 있음
-
참고1 - Adversarial Attack (Ref[2]): 아래 그림은 이미지 분류 모델이 판다 사진은 판다라고 잘 예측하는 반면, 노이즈를 주입했을 뿐 같은 판다 사진은 판다라고 예측하지 못하고 긴팔원숭이라고 예측한 사례임. 이와 같이 인풋 데이터 혹은 모델 구조에, 아웃풋 라벨과는 상관없는 오염/공격이 가해져 아웃풋이 바뀌어버릴 때 해당 오염/공격을 Adversarial Attack이라고 정의함

-
-
최근 그래프 내 인접한 노드 사이의 정보 전달을 Neural ODE를 통해 표현하고 GNN을 Graph Neural Flow라는 동적 시스템의 변화로 해석하기 시작함. Graph Neural Diffusion이 기존 GNN 대비 topology perturbation에 덜 취약하다는 내용의 연구가 나오고 있으나, 관련 이론적 토대는 부족한 상황임
-
참고1 - Neural ODE (Ref[3]) : RNN 등 특정 시점의 hidden state가 과거의 hidden state에 대한 함수로 표현되는 아키텍처는 hidden state가 $h_ {t+1} = h_ {t} + f(h_ {t}, \theta _{t})$ 수식을 따라 변화함. 즉 시점과 시점 간 차이 (step size) 가 크고 시점들 (layer) 개수는 적은 이산적인 형태를 가지고 있음. Neural ODE는 여기서 step size를 무한히 줄이고 layer 개수를 늘려 이산적인 형태의 hidden state 변화를 연속적인 형태인 $dh(t)/dt = f(h(t), t, \theta)$ Ordinary Differential Equation으로 나타내어, hidden state 업데이트를 이미 수학/물리에서 많이 다뤄진 미분방정식 푸는 문제로 바꿈. 아래 그림과 같이 레이어가 깊어질수록 ODE Network는 기존 RNN 대비 hidden state가 연속적으로 변화함:
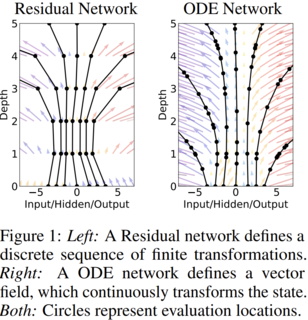
-
참고2 - Graph Neural Flow: 위 Neural ODE를 그래프 노드 간 message passing에 활용한 형태의 GNN
-
-
해당 논문은 아래 두 가지 논의를 통해 동적 시스템/물리에서 얻은 인사이트를 Node 간 정보 전달 구조에 적용하여 adversarial attack에 robust한 GNN을 만들고자 함. 직관적으로, 노드 간 Message Passing을 어떤 연속적인 형태의 미분방정식 (Graph Neural Flow)을 따르도록 해야 GNN이 그래프 노드나 구조에 가해지는 공격 (Adversarial Attack)에도 안정적인 추론을 수행하도록 할 수 있는가? 가 해당 논문이 풀고자 하는 연구 문제임
- GNN 관점에서의 Stability 논의 및 기존 Graph Neural Flow의 Stability 점검
- Hamiltonian Flow를 활용하여 Robustness를 높인 HANG (-quad) Graph Neural Flow 제안
1. Stability of Graph Neural Flows
BackGround1. 동적시스템과 Graph Neural Flow
동적 시스템이란 시간에 따라 동적으로 변화하는 미분방정식 시스템임. 본 논문에서는 시스템의 $z$의 변화량을 $z$ 및 파라미터 $\theta$에 관한 함수 $f$로 정의하여 다음과 같이 표현할 수 있음: $dz / dt = f_ {\theta}(z(t))$ GNN 관점에서 이는 node feature $z(t)$가 그래프 topology $f_ {\theta}$에 따라 변화하는 과정을 연속적으로 표현한 것으로 이해할 수 있음.
Background2. 동적시스템과 Graph Neural Flow의 Stability
동적 시스템의 안정성 관련 다양한 관점과 정의가 존재함
- 관점 1. 어떤 시점 $t$에서 노드 $z$에 발생한 perturbation에도 노드 $z$의 trajectory가 안정적으로 유지되는가? *equilibrium - $z$의 trajectory가 변화하지 않는 지점. Formally, $dz / dt = f_ {\theta}(z(t)) = 0$을 만족하는 $z$
- BIBO Stability - 시점 $t$가 bounded 할 때, 노드 $z(t)$ trajectory도 bounded하다면 해당 시스템은 BIBO Stable하다고 정의함. Formally, BIBO stable if for any bounded input, there exists a constant $M$ s.t. $\vert \vert z(t) \vert \vert < M$ for all $t \geq 0$
- Lyapunov Stability - equilibirum 노드 $z_ e$에서 충분히 가까운 $z(0)$으로부터 trajectory가 시작할 때, 이후 모든 시점 $t$에서의 노드 $z(t)$ trajectory가 $z_ e$에 가깝게 유지된다면 해당 시스템은 Lyapunov Stable하다고 정의함. Formally, Lyapunov stable if for every $\epsilon > 0$, there exists $\delta > 0$ s.t. $\vert \vert z(0) - z_ {e} \vert \vert < \delta \implies \vert \vert z(t) - z_ {e} \vert \vert < \epsilon$ for all $t \geq 0$
- Asymptotic Stability - equilibrium 노드 $z_ e$에서 충분히 가까운 $z(0)$으로부터 trajectory가 시작할 때, $z(t)$가 Lyapunov stable 하고, 최종적인 $z(t)$ trajectory (as t goes to infinity) 가 $z_ e$에 무한히 가까워진다면 해당 시스템은 Asymptotic Stable하다고 정의함. Formally, Asymptotic stable if Lyapunov Stable & there exists $\delta’ > 0$ s.t. $\vert \vert z(0) - z_ {e} \vert \vert < \delta’ \implies lim_ {t \rightarrow \infty}\vert \vert z(t) - z_ {e} \vert \vert = 0$
- 관점 2. $f_ {\theta}$에 대한 attack, 즉 노드가 아닌 시스템 자체의 변동이 생겼을 때 노드 $z$의 trajectory가 안정적으로 유지되는가?
- Structural Stability - 그래프 topology ($\theta$) 가 perturb 되었을 때의 노드 trajectory $z(t)$를 perturb 되지 않았을 때의 $z(t)$로 매핑하는 homeomorphism이 존재한다면 해당 시스템은 Structural Stable하다고 정의함
- 관점 3. 시스템 내 항상 일정하게 유지되는 물리적 값이 있는가?
- Conservative Stability - 노드 $z(t)$ trajectory를 따라 유지되는 절대적인 값이 존재할 경우 해당 시스템은 Conservative Stable하다고 정의함
Discussion 1. Node Perturbation Stability 한계
Node Perturbation에 따른 안정성, 특히 Lyapunov Stability의 성립을 보임으로써 시스템이 Adversarial Attack에 강하다고 주장하는 기존 연구가 많음. 본 논문은 GNN 관점에서 해당 Stability만으로는 기존 주장을 뒷받침하기 어렵다는 것을 다음 미분방정식 예시를 통해 제시함:
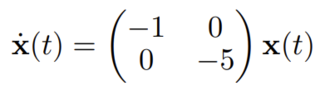
-
위 ODE는 x의 변화량과 x를 매핑하는 행렬이 시간에 따라 변화하지 않으며, 해 $x(t) = x_ 1(0) e^ {-t}e_ 1 + x_ 2(0) e^ {-5t}e_ 2$ 를 구할 수 있음. 해에서 나타나듯이 해당 행렬의 eigenvalue는 모두 음수로 equilibrium point인 x(t) = 0에 exponential하게 가까워짐. 따라서 Lyapunov (+Asymptotic) Stability를 만족함.
-
그러나 해당 시스템이 실제 GNN 관점에서 안정적이라고 이야기할 수 없음
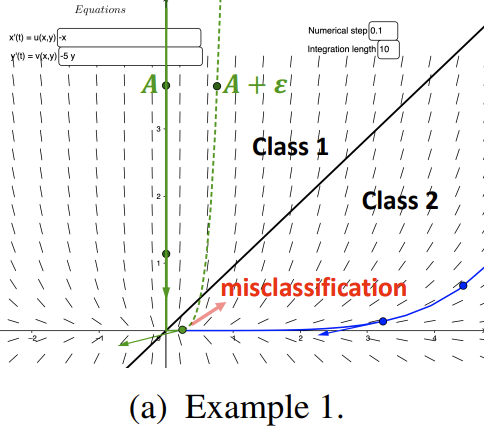
그림에서처럼 Class 1과 Class 2를 구분하는 Node Classification Task에서 Class 1과 Class 2에 해당하는 trajectory가 모두 원점을 Equilibrium point로 가지며, 이는 Lyapunov Stable 하다고 가정함. 이 때 원점으로부터 충분히 가까운 어떤 노드 A가 A + $\epsilon$ 으로 perturb되었을 때, 그림 내 초록색 trajectory를 따르게 되어 어떤 시점 t에 대해서는 Class 2로 잘못 분류될 수 있음. 또한 여기에 Structural Stability가 추가되더라도 오히려 해당 Stability 때문에 Equilibrium Point 개수가 1개라는 사실이 유지되므로, 초록색 trajectory와 파란색 trajectory는 여전히 서로 다른 equilibrium가 아닌 같은 원점 equilibrium으로 수렴하여 안정성이 높아지지 않음
따라서 더 robust한 GNN을 만들기 위해서는 Lyapunov (+ Asymptotic) 혹은 Structural Stability 뿐만 아니라 시스템 자체에 대한 Conservative Stability를 가지고 있는지 함께 고려하는 것이 필수적임
Discussion 2. 기존 Graph Neural Flow의 Stability
본 논문에서는 기존 Graph Neural Flow 중 Message Passing에 사용되는 ODE 미분방정식 수식에 따라 4가지를 소개하고 있음. 앞서 살펴본 Stability 정의를 기준으로 이들이 실제로 robust한 stability를 가지고 있는지 점검하고자 함.
GRAND: heat diffusion 사용
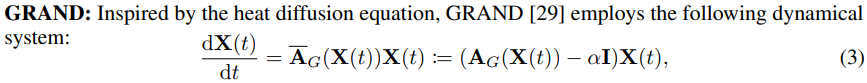
$A_ G(X(t))$의 time-variance 유무에 따라 각각 GRAND-nl, GRAND-1로 구분되며, 특히 GRAND-nl의 $A_ G = a_ G(x_ i(t), x_ j (t))$ 는 시간에 따른 노드 $x_ i$, $x_ j$ 간 유사성을 계산하는 Attention Matrix로 해석할 수 있음.
Theorem1. GRAND는 특정 조건 아래에서 다음과 같은 BIBO, Lyapunov, Asymptotic 및 Conservative Stability를 만족함
- (GRAND-nl) $A_ G(X(t))$가 doubly stochastic일 때
- $\alpha \geq 1$일 경우: BIBO, Lyapunov
- $\alpha > 1$일 경우: global asymptotic
- (GRAND-1) $A_ G$가 constant column 혹은 row stochastic일 때
- $\alpha > 1$일 경우: global asymptotic
- $\alpha = 1$ & Strongly Connected일 경우: BIBO, Lyapunov
- (GRAND-1) $A_ G$가 constant column-stochastic이고 $\alpha = 1$일 때
- 기본적으로: conservative
- 그래프가 aperiodic, aperiodic, strongly connected, perturbations on X(0) ensure unaltered column summations일 경우: asymptotic
직관적으로, $A_ G$의 stochasticity 및 $\alpha$의 크기 조건은 Trajectory X(t)의 변화량을 결정하는 행렬의 원소가 곱셈 연산을 지속하더라도 X(t)를 안정하게 만들어주는 제약 조건임.
BLEND: GRAND + positional encoding
positional encoding의 영향이 없다면 (e.g. constant로 세팅) GRAND와 동일 구조로, 위에서 증명된 특정 조건 아래에서의 BIBO 및 Lyapunov Stability 가짐
GraphCON: oscillatory dynamics 사용

activation function $\sigma$가 identity이고 coupling function $F_ \theta (X(t), t)$ 이 어떤 constant matrix $A$와 $X(t)$의 곱으로 표현될 수 있다면 z(t) trajectory 위에서 Dirichlet 에너지가 일정하게 유지되어 Conservative Stability 가짐
GraphBel: beltrami flow 사용
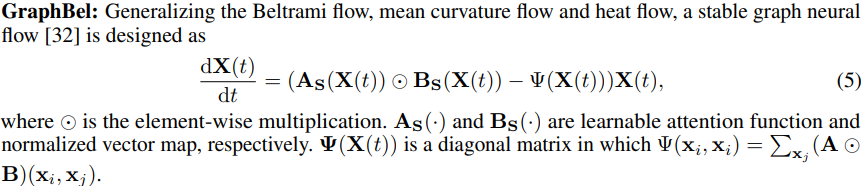
$\Psi (X(t)) = B_ S(X(t)) = I$라면 GRAND와 동일 구조로, 역시 특정 조건 아래에서의 BIBO 및 Lyapunov Stability 가짐
Discussion1, 2에 정리된 내용을 통해 Lyapunov (+Asymptotic), Structural Stability 만으로는 Node Classification 등의 Task에서 Adversarial Attack을 막기에 부족하다는 점을 예시적으로 보임. 그러나 기존 연구에서 제시된 Graph Neural Flow는 대부분 특정 조건 아래에서만 BIBO, Lyapunov, Conservative Stability를 만족함. 따라서 해당 Flow들이 Conservative Stability를 (추가 조건 없이도) 만족하도록 하기 위한 고민이 필요함
2. Hamiltonian Flow $\rightarrow$ HANG (-quad)
Background1. Hamiltonian Flow
Hamiltonian 역학은 자연계의 다양한 multi-agent 시스템 (e.g. Electromagnetic field, double pendulum) 의 변화를 포지션 벡터 $q$와 모멘텀 벡터 $p$의 쌍, $(q,p)$의 상태 변화로 설명함. 이 때 $q$, $p$는 어떤 Hamiltonian $H(p,q)$에 대하여, $\dot{q} = \partial H / \partial p$, $\dot{p} = - \partial H / \partial q$ (Hamiltonian Flow) 를 만족하고, 모든 상태에서 $H$는 일정하게 유지되며 이는 시스템 내 agent의 위치와 속도가 변화하더라도 보존되는 시스템 내 에너지로 이해할 수 있음
Method 1. Hamiltonian Flow의 GNN 적용
본 논문은 아래와 같은 아키텍처를 기반으로 Hamiltonian Flow를 Graph Neural Flow로 활용하여 GNN 내 Hamiltonian H에 해당하는 값이 일정하게 유지되도록 만들고, Conservative Stability 및 Robustness를 높이고자 함. 간단히, 그래프 노드별 피처 및 모멘텀 벡터가 Hamiltonian Flow를 따르도록 ODE Solver를 사용하여 변형하고, 이를 Downstream task에 활용함
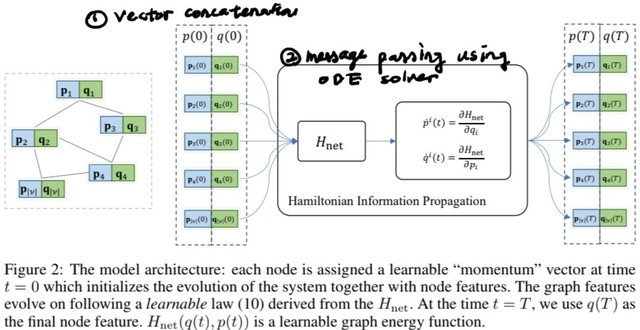
-
Vector Concatenation: 시점 t에서 그래프의 노드 피처를 r-dimensional feature vector $q(t)$ 와 momentum vector $p(t)$ 로 정의하며 모든 노드의 $q(t)$와 $p(t)$를 concatenation하여 그래프 전체의 특성 및 모멘텀을 나타냄
-
Message Passing using ODE solver: initial condition $(q(0)_ {concat}, p(0)_ {concat})$ 에서 시작하여 Hamiltonian Flow $\dot{q} = \partial H / \partial p$, $\dot{p} = - \partial H / \partial q$에 따라 노드 간 정보가 propagate 되도록 함. initial condition과 governing ODE 미분방정식이 주어진 상황이므로 ODE solver를 사용하여 어떤 시점 t에서의 $(q(t)_ {concat}, p(t)_ {concat})$를 구할 수 있음. 이 때 $H$는 그래프를 인풋하면 양의 실수 숫자를 아웃풋하는 learnable 함수로 정의함 (method 2에서 구체화)
-
Projection to extract Node Feature: 일정 시간 동안의 propagation 이후 terminal time $T$의 노드 피처 $(q(T)_ {concat}, p(T)_ {concat})$에 projection mapping $\pi$를 적용하여 노드별 feature vector $q(T)_ {concat}$를 구함
-
Application to Downstream Tasks: $q(T)_ {concat}$를 decompress하여 각 노드별 $q(T)$를 추출하고 해당 노드 피처를 downstream task에 활용
*참조 - Appendix D: 직관적으로, ODE Solver 내 시간 개념은 GNN 내 이산적인 레이어 형태, $q(t)$는 노드 피처, $p(t)$는 노드 피처가 전 레이어에서 후 레이어로 이동함에 따라 변화하는 정도로 이해할 수 있음. 따라서 시간이 지나도 일정하게 유지되는 절대적인 값 Hamiltonian $H$가 있다는 것은, 레이어가 아무리 깊어지더라도 노드 피처와 피처의 변동이 어떤 규제를 따라서만 변화하도록 제약을 걸어주는 역할을 함. 이런 구조 덕분에 노드 피처 혹은 그래프 위상에 대한 Attack이 모든 레이어의 그래프 전체에 작용하는 것이 아닌 이상 $q(t)$와 $p(t)$가 규제에 맞게 변화하며 완화됨
Background2. Hamiltonian Flow의 Stability
Hamiltonian의 정의에 의해 Hamiltonian Flow를 Graph Neural Flow로 사용하면 Conservative Stability를 반드시 가짐. 추가적으로, Lagrange-Dirichlet Theorem에 의해 Hamiltonia $H$의 형태가 특정 조건을 만족하도록 변형하면 Lyapunov Stability 또한 가짐이 이론적으로 증명됨. 즉 Hamiltonian $H$를 아래 Theorem 2, 3에 따라 잘 설정하면 Stability를 높일 수 있음
Theorem 2. Hamiltonian Flow $\dot{q} = \partial H / \partial p$, $\dot{p} = - \partial H / \partial q$ 을 만족하는 $H(q,p)$와 $(q,p)$로 정의된 그래프 시스템은 Conservative Stability를 가짐. 또한 아래 두 가지 조건1, 2를 추가적으로 만족하면 BIBO Stability를 가짐
- Conservative Stability에 대한 증명: $\frac{dH}{dt} = \sum_ {i=1}^n (\frac {\partial H}{\partial q_ i} \dot q_ i + \frac {\partial H}{\partial p_ i} \dot p_ i) = \sum_ {i=1}^n(\frac {\partial H}{\partial q_ i} \frac {\partial H}{\partial p_ i} + \frac {\partial H}{\partial p_ i} (- \frac {\partial H}{\partial q_ i})) = 0$
- 조건1: $(q,p)$ bounded $\implies$ $H(q,p)$ bounded
- 조건2: $(q, p) \rightarrow \infty \implies H(q,p) \rightarrow \infty$
Theorem 3. (Lagrange-Dirichlet Theorem) $z_ {e}$를 $\dot{q} = \partial H / \partial p$, $\dot{p} = - \partial H / \partial q$을 만족하는 미분방정식 시스템의 locally quadratic equilibrium이라 하고, 아래 3가지 조건을 모두 만족하면 $z_ {e}$는 Lyapunov stable함
- $H = T(q,p) + U(q)$ 형태로 표현됨
- $T(q,p)$ positive definite & quadratic function of p
- $z_ {e}$가 $U(q)$의 strict local minimum
*참고 - GraphCON 해석: Undirected Graph $(G, V, E)$를 활용하는 GNN 세팅에서 노드 피처 $q(t)$에 대한 에너지를 $\frac{1}{\vert V \vert} \sum_ {i} \sum_ {j \in N(i)} \vert \vert q_ i (t) - q_ j (t) \vert \vert^ 2$로 Dirichlet 에너지와 같이 정의할 수 있음. (노드별 주변 노드 사이와의 피처 차이 $l2$ norm의 평균) 기존 연구 중 GraphCON은 Dirichlet 에너지를 일정하게 유지하는 방향으로 노드 피처가 변화하는데, Dirichlet 에너지는 Hamiltonian 에너지 중 에너지가 $q$에 따라서만 변동하는 특수한 경우로 볼 수 있음. 따라서 GraphCON은 본 논문에서 제시하는 Hamiltonian Flow를 활용하는 Graph Neural Flow의 한 종류로 해석할 수 있음
Method 2. H 구체화 통한 HANG (-quad) 제시
Hamiltonian의 Flow를 GNN에 적용하기 위한 아키텍처와 함께, 기존에 learnable 함수라고만 정의했던 Hamiltonian $H$를 구체적으로 제시하고자 함. 이 때 Background 2에 제시된 Hamiltonian Flow Stability에 대한 정리 Theorem 2, Theorem 3를 바탕으로, GNN이 Conservative Stability뿐만 아니라 Lyapunov Stability 또한 갖추도록 $H$를 설정하고자 함
Vanilla HANG (Conservative + BIBO) 전체 노드에 대한 피처 벡터와 모멘텀 벡터의 concatenation에 GCN, tanh, GCN을 적용한 결과 벡터의 l2 norm으로 $H$를 정의함. 이론적으로 $H$는 $(q, p)$에 대한 함수이기만 하면 어떤 형태여도 Conservative Stability를 만족하나, 그래프 임베딩을 사용하여 표현력을 높이고자 한 것으로 보임 (수식에서 $r$은 $q$, $p$ 벡터의 dimension, $\vert V \vert$는 그래프의 노드 개수)
- $H$ 형태: $H_ {net} = \vert \vert (g_ {gcn2} \circ tanh \circ g_ {gcn1}) (q_ {concat}, p_ {concat}) \vert \vert_ 2$
- layer 형태: $g_ {gcn1} : \mathbb{R}^ {2r \times \vert V \vert} \rightarrow \mathbb{R}^ {d \times \vert V \vert}, g_ {gcn2} : \mathbb{R}^ {d \times \vert V \vert} \rightarrow \mathbb{R}^ {\vert V \vert}$
위 $H$ 사용 시 그래프 시스템은 Background2. Theorem2. 에 의해 Conservative Stability와 BIBO Stability를 가짐 ($dH / dt = 0$로 $H$는 일정하고 (Conservative), 따라서 초기 $(q, p)$가 bounded (infinite) 라면 $H$ 또한 bounded (infinite) 함 (BIBO))
Quadratic HANG (Conservative + BIBO + Lyapunov) $H$를 $T(q,p) + U(q)$로 정의하고 Background2. Theorem3. 조건1,2를 아래와 같이 만족하도록 한다면, 기존 Conservative, BIBO 뿐만 아니라 Lyapunov Stability 또한 가지도록 할 수 있음
-
조건 1 - $T(q,p)$ positive definite & quadratic function of $p$: $T(q,p) = \sum_ k p_ k^T(A_ G (q_ k, q_ k)A_ G^T (q_ k, q_ k) + \sigma I)p_ k \, (\sigma > 0)$ 형태로 정의하여 $p$에 대한 quadratic function 및 positive definiteness를 만족하도록 할 수 있으며, 이 때 $A_ G$는 learnable adjacency 혹은 attention 행렬로 정의하여 노드 간 정보 교환을 반영하게 만들 수 있음
-
조건 2 - locally quadratic equilibrium $z_ {e}$가 $U(q)$의 strict local minimum: $U(q) = \vert \vert (sin \circ g_ {gat}) (q_ {concat}) \vert \vert_ 2$ 와 같이 정의, GAT layer를 포함하여 표현력을 높이고, $sin$을 activation 함수로 사용하여 $sin$이 local minimum 이 되는 지점들, 즉 Lyapunov Stable한 equilibrium points가 될 수 있는 후보들을 최대한 많이 만들고자 함. 만약 $U(q) = \vert \vert sin (q_ {concat}) \vert \vert_ 2$와 같은 형태로 정의한다면 표현력이 낮아 $U$가 가질 수 있는 값에 너무 큰 제약을 걸어버리고, $U(q) = \vert \vert q \vert \vert_ 2$와 같은 형태로 정의한다면 local minimum이 없어 $H$가 Lyapunov Stability를 가지지 못함
Experiments
Graph Injection Attack (GIA)
- Attack 알고리즘: PCD-GIA, TDGIA, MetaGIA
- 데이터셋: 인용 네트워크 (Cora, Citesser, Pubmed), Coauthor academic network, Amazon co-purchase network, Ogbn-Arxiv
- 학습 및 평가: HANG과 타 Baseline GNN에서 attack 유무에 따라 Node Classification Task의 Accuracy가 얼마나 달라지는지 확인
- 결과: 인용 및 Coauthor Academic network 데이터셋 대상 injection, evasion, non-targeted attack 유무에 따른 inductive learning에서의 성능 차이를 확인했을 때, HANG 및 HANG-quad가 타 baseline 대비 attack에 대한 robustness가 높음 (clean과 비교하여 PGD, TDGIA, MetaGIA attack 시 성능 감소가 제일 적음)
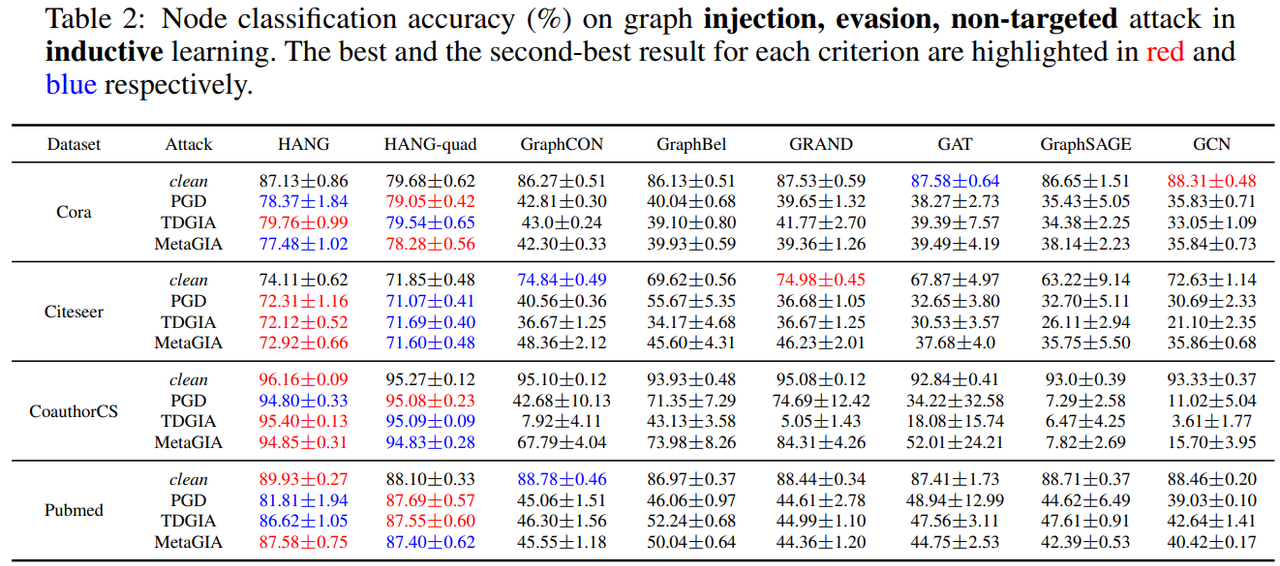
또한 Amazon co-purchase 및 Ogbn-Arxiv 데이터셋 대상 injection, evasion, targeted attack 적용 시 inductive learning에서의 성능을 확인했을 때, HANG 및 HANG-quad의 attack에 따른 성능 변동이 타 baseline 대비 적은 편

Graph Modification Attack
- Attack 알고리즘: Metaattack (+ ProGNN 세팅)
- 데이터셋: Polblogs, Pubmed
- 학습 및 평가: HANG과 타 Baseline GNN에서 attack 정도 (엣지 변경의 비율을 0%에서 25%까지 조정) 에 따라 Node Classification Accuracy가 어떻게 달라지는지 확인
- 결과: modification, poisoning, non-targeted attack 정도에 따른 transductive learning에서의 성능 차이를 확인했을 때, HANG-quad가 타 baseline 대비 attack에 대한 robustness가 높음
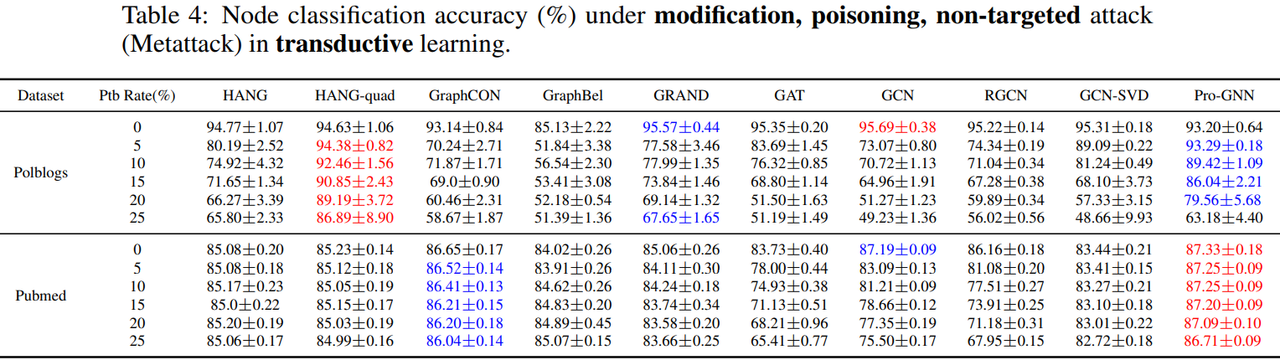
추가 실험 (Appendix C)
- White-Box, Netattack 추가 실험에서도 HANG-quad의 robustness가 두드러짐
- ODE Solver 종류에 따른 HANG 및 HANG-quad의 robustness 변동은 크지 않음
- HANG 및 HANG-quad의 Computation Time은 타 baseline 대비 높은 편. 그러나 GCNGuard와 같이 Adversarial Attack을 막는 모델 대비 낮음
- HANG과 Adversarial Training 및 GNN Defense Mechanism을 함께 적용했을 경우 robustness 증가함
Conclusion
-
GNN 관점에서의 Stability 논의 및 기존 Graph Neural Flow의 Stability 점검: 기존 연구 대부분 특정 조건 아래에서만 BIBO/Lyapunov/Conservative Stability를 만족함. 특히 Lyapunov Stability 만으로는 GNN Attack에 robust하다고 말할 수 없음을 예시적으로 보임
-
Hamiltonian Flow를 활용하여 Robustness를 높인 HANG (-quad) Graph Neural Flow 제안: 이론적으로, HANG은 노드의 정보들이 propagation 되는 동안 Hamiltonian $H(p, q)$는 일정하게 유지되어 Conservative Stability를 가짐. HANG-quad는 Lagrange-Dirichlet Theorem에 따라 설계되어 Lyapunov Stability를 추가적으로 가짐. 실험적으로, Node Classification Task에서 Graph Injection, Modification Attack에 대해 HANG, HANG-quad의 성능 감소가 타 GNN 대비 적음을 보이며 이론적으로 증명된 Conservative 및 Lyapunov Stability의 효과를 확인함
Comment
-
물리 아이디어 (동적 시스템 안정성, Hamiltonian 역학) 를 바탕으로 GNN Adversarial Attack 문제에 대한 이론적인 해결법을 제시하여 흥미로움
-
Lyapunov Stability로는 부족하다는 것에 대한 분석은 있지만 Conservative Stability가 필요하다는 주장에는 직관/성능 실험/node label 변화 관찰 외의 자세한 분석이 없어서 아쉬웠음. (특히 Attack 적용 유무에 따라 ODE solver 내의 layer들에서 실제 노드의 $(q, p)$가 어떻게 변화하는지 궁금함)
Author Information
- Author: Sungyoung Kim
- Affiliation: Brain & Machine Intelligence Lab, Graduate School of Data & Science
- Research Topic: Graph Neural Network, Dynamical System
Reference & Additional Materials
-
[1] K. Zhao, Q. Kang, Y. Song, R. She, S. Wang, W. Tay, “Adversarial Robustness in Graph Neural Networks: A Hamiltonian Approach”, New Orleans, USA, NeurIPS 2023 (Github Implementation: https://github.com/zknus/NeurIPS-2023-HANG-Robustness)
-
[2] I. Goodfellow, J. Shlens, C. Szegedy, “Explaining and Harnessing Adversarial Examples”, Mountain View, CA, United States, ICLR 2015
-
[3] R. Chen, Y. Rubanova, J. Bettencourt, D. Duvenaud, “Neural Ordinary Differential Equations”, Montreal, Canada, NeurIPS 2018