[ICML 2024] Recurrent Distance Filtering for Graph Representation Learning
1. Motivation
Message Passing Neural Networks(MPNNs)의 한계점
MPNNs은 각 레이어마다 이웃 노드들의 message를 aggregate한다. 따라서 k-hop만큼 떨어진 이웃 노드의 정보에 접근하기 위해서는 k개의 MPNN 레이어를 필요로 한다. 그러나, 이로 인해 노드의 receptive field가 k에 기하급수적으로 증가하게 된다. 이렇게 증가하는 receptive field는 고정된 크기의 representation에 담기게 되고, 이는 정보 손실을 야기한다. 이러한 현상을 over-squashing이라고 하며, 이는 MPNNs의 핵심적인 한계점인 long range interaction을 잘 포착하지 못하는 특성의 원인이 된다.
Graph Transformers(GTs)
GTs는 MPNNs가 해결하지 못하는 long range interaction을 잘 포착하고자 고안된 모델이다. GTs는 모든 노드에 대해 global attention을 적용하여, 모든 노드 쌍에 대한 관계를 포착할 수 있다. 그그러나 global attention에서 노드 수의 제곱에 비례하는 quadratic complexity를 요구하기 때문에, 효율성 측면에서 부족하다.
2. Proposed Model: GRED Layer
Graph Recurrent Encoding by Distance(GRED)는 long range interaction을 잘 포착하면서도 효율적인 구조로서 고안된 모델이다. Transformer 대신 linear RNN을 활용하고, multiset aggergation을 통해 RNN에 넣어줄 적절한 input을 shortest-path distance 기반으로 만들어 준다.
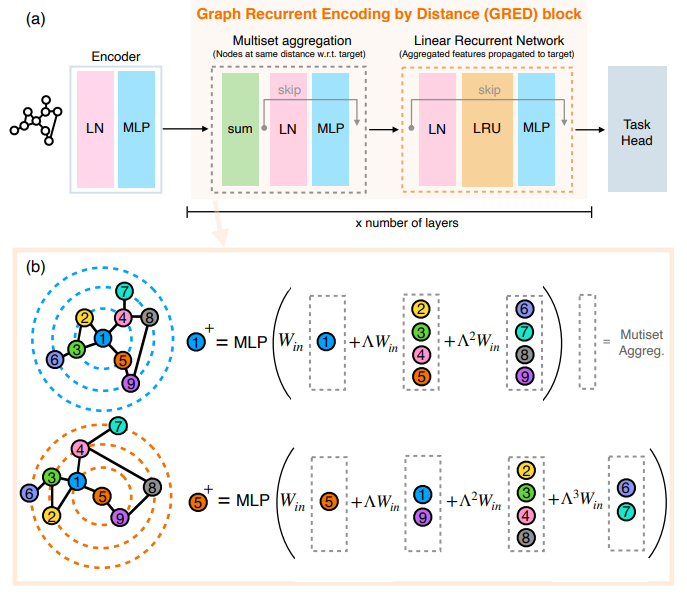
Multiset Aggregation
이전 layer의 output $\boldsymbol h_{u}^{(l-1)}$에 대해서, GRED는 node의 각 hop 별 이웃들의 정보를 취합하는 multiset aggregation을 먼저 수행한다. $\boldsymbol{x}_ {v,k}^{(l)} =\mathrm{AGG}\left( {!{ \boldsymbol h_ {u}^{(l-1)}\;|\;u\in\mathcal N_ {k}(v) }!} \right)$ 이 결과물 $\boldsymbol{x}_ {v,k}^{(l)}$ 은 노드 $v$의 $k$-hop 이웃들의 정보를 담은 representation vector이며, 이를 $k=0,\dots,K$ 에 대해 수행하여 최종적으로 $(\boldsymbol{x}_ {v,0}^{(l)},\boldsymbol{x}_ {v,1}^{(l)},\dots,\boldsymbol{x}_ {v,K}^{(l)})$ 의 형태의 sequence를 얻을 수 있다. Aggregation은 permutation-invariant neural network(DeepSet이나 GIN)의 아이디어를 활용하여 sum aggregation을 사용하며, 실제로는 다음과 같은 식으로 계산된다. \(\boldsymbol{x}_ {v,k}^{(l)} =\mathrm{MLP}_ {2}\left( \sum_ {u\in\mathcal N_k(v)}\mathrm{MLP}_ {1}\left( \boldsymbol h_ {u}^{(l-1)} \right) \right)\in\mathbb R^d\)
Linear Recurrent Network
Linear Recurrent Network(LRU)는 SSM에서 착안한 RNN 모델로, 기존 매 update마다 있던 activation함수를 제거하여 parallel한 processing이 가능하도록 하는 효율적인 모델이다. Multiset Aggregation에서 생성된 sequence는 LRU의 각 step으로 다음과 같이 입력된다. $\boldsymbol{s}_ {v,k}^{(l)}=\boldsymbol A\boldsymbol{s}_ {v,k-1}^{(l)}+\boldsymbol B\boldsymbol{x}_ {v,K-k}^{(l)}$ 식에서 볼수 있듯이 $\boldsymbol{x}_ {v,K}^{(l)}$ 부터 거꾸로 넣어주는데, 이는 멀리서 ($K$-hop)부터 타겟 노드 ($v$)까지 정보가 모여들기 때문이다. LRU에서와 같이, 위의 RNN연산을 $\boldsymbol A$를 대각화함으로써($\boldsymbol A=\boldsymbol V \mathbf{\Lambda}\boldsymbol V^{-1}$) 효율적인 형태로 바꾼다. $\boldsymbol{s}_ {v,k}^{(l)}=\mathbf {\Lambda}\boldsymbol{s}_ {v,k-1}^{(l)}+\boldsymbol {W}_ {\mathrm{in}}\boldsymbol{x}_ {v,K-k}^{(l)}\rightarrow\boldsymbol{s}_ {v,k}^{(l)}=\sum_ {k=0}^{K}\mathbf {\Lambda}^k\boldsymbol {W}_ {\mathrm{in}}\boldsymbol{x}_ {v,k}^{(l)}$ 결과적으로 $k$-hop에 있는 노드들의 representation은 $\mathbf {\Lambda}^k$ 가 곱해지고, 이를 타겟 노드로부터 $\mathbf {\Lambda}$로 “filter over hops”을 수행하는 것이라고 설명한다.
Output of GRED Layer
최종적으로는 LRU의 마지막 hidden state에 대하여 간단한 non-linear transform(MLP)를 적용하여 다음 GRED layer의 입력으로 넣어준다. $\boldsymbol{h}_ {v}^{(l)}=\mathrm{MLP}_ {3}\left( \mathfrak{R}\left[\boldsymbol {W}_ {\mathrm{out}}\boldsymbol{s}_ {v,K}^{(l)}\right] \right)$ GRED로 생성된 노드들의 representation을 활용하여 node classification, graph classificatino과 같은 다양한 graph task를 수행할 수 있다.
3. Expressiveness Analysis
GRED는 LRU의 도움으로 기존 MPNN의 한계인 1-WL를 뛰어넘는 expressivity를 가질 수 있음을 보인다. 요약하자면, GRED는 노드의 각 $k$-hop 이웃들에 대한 injective mapping을 수행 가능하고, 이는 논문에 언급된 다음 정리로 결론지어진다.
Corollary 4.3 (Expressiveness of GRED) When $K>1$, A wide enough GRED layer is more expressive than any 1-hop message passing layer.
4. Experiments
실험에서 GRED의 성능을 다양한 MPNNs 모델들 그리고 GTs 모델들과 비교한다.
Datasets
자주 활용되는 Benchmarking graph neural networks(Benchmarking GNN)의 4가지 데이터셋과, 큰 그래프에 대한 성능 비교를 위해 Long Range Graph Benchmark(LRGB)의 2가지 데이터셋을 활용한다.
Node Classification 데이터셋: PATTERN, CLUSTER
Graph Classification 데이터셋: MNIST, CIFAR10
Graph Regression 데이터셋: ZINC 12k
LRGB (Graph Classification) 데이터셋: Peptides-func, Peptides-struct
아래는 각 데이터셋에 대한 실험 결과이다.
Benchmarking GNNs
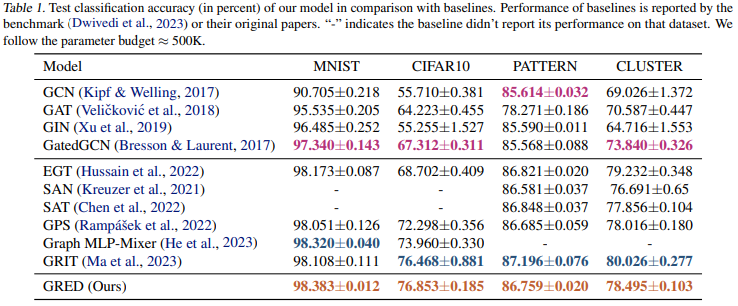 (metric: accuracy)
(metric: accuracy)
ZINC 12k, LRGB
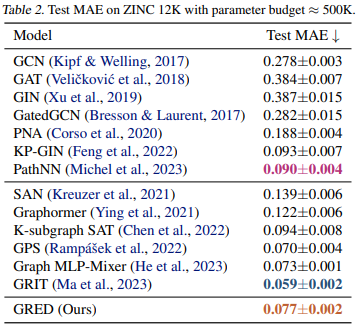
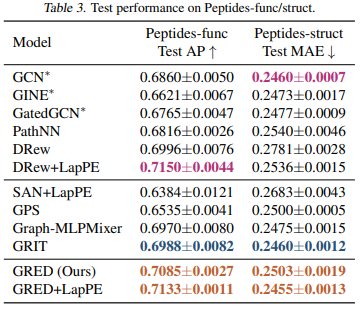
- Graph Transformer 모델들이 MPNN 모델보다 좋은 성능을 보이는 경향성이 있다.
- GRED가 가장 좋은 성능을 보이는 Graph Transformer 모델과 comparable한 성능을 보인다. 그러나 GRED는 GTs에서 필수적인 positional encoding이 필요가 없으며, 훨씬 효율적인 모델이라는 점에서 강점이 있다.
Training Time
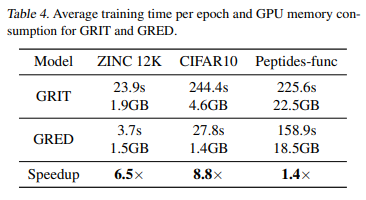
GRED의 효율성을 검증하기 위해, Graph Transformer의 SOTA 모델인 GRIT와 training time, GPU 메모리 소비량을 비교하였다. 데이터셋 종류에 따라 그 정도는 다르지만, GRED가 두 방면에서 모두 어느정도 효율적인 모델임을 확인할 수 있다. 다만, 큰 그래프 데이터(Peptides-func)에서는 오히려 두 모델 간의 차이가 크지 않기 때문에, 다양한 종류의 그래프에서 확실한 효율성 개선이 있는지는 추가적인 검증이 필요하다.
Sequence 길이($K$)에 대한 분석
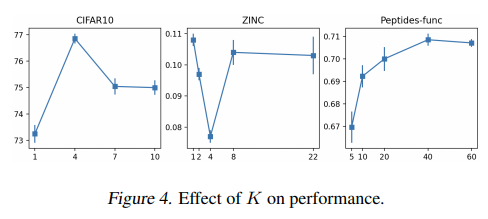
논문에서는 추가적으로 multiset aggregation에서 고려하는 최대 hop에 따라 성능이 어떻게 달라지는지 확인하였다. 가장 높은 성능을 보이는 $K$값은 데이터셋 종류에 따라 다른 경향을 보였는데, 이는 각 데이터셋마다 그래프의 크기, 지름과 같은 구조에 영향을 받는다고 해석할 수 있다. $K$가 그래프의 지름보다 커지게 되면, 같은 노드가 중복해서 등장하는 등 문제가 발생하기 때문에 논문에서는 $K$가 1과 그래프의 지름 사이에서 최적의 성능을 보인다고 분석한다.
5. Conclusion
- 본 논문은 MPNNs의 long range interaction 해결 문제와 GTs의 높은 computatinal cost의 문제를 해결하기 위한 모델인 GRED를 제시하였다. GRED는 $k$-hop 이웃 노드에 대한 aggregation을 통한 senquence를 생성하고, 이를 LRU input으로 활용하여, 효율적이면서도 long range interaction을 잘 해결할 수 있는 구조를 설계했다.
- 본 논문에서는 GRED의 표현 능력, 성능, 그리고 효율성을 여러 이론적 분석과 실험을 통해 검증하였다.
- 그래프 머신러닝에서 MPNN이나 Transformer을 기반으로 한 것이 아닌 새로운 approach를 제시하였다.