[AAAI-2024] Label Attentive Distillation for GNN-Based Graph Classification
1. Introduction and Motivation
Graph Neural Networks (GNNs) have gained substantial traction in recent years due to their powerful ability to model graph-structured data. They are used extensively in applications such as social networks, recommendation systems, molecular biology, and more. Traditional GNNs, while effective, face limitations when it comes to graph-level tasks, particularly in graph classification. Aiming to improve the performance, this study introduces a novel approach, Label Attentive Distillation (LAD-GNN).
The key problem in existing GNN approaches can be named to be embedding misalignment. Traditional GNN models perform node-level feature aggregation without considering graph-level label information. This results in embeddings that do not align well with their corresponding graph labels. The misalignment of these embeddings reduces the discriminative power of graph representations, leading lessened classification accuracy.

Figure 1. The shortcomings of the conventional pipeline of GNN-based graph classification.
To address this issue, the authors proposed the LAD-GNN algorithm, which introduces a distillation framework where a “teacher” model guides a “student” GNN. The teacher model uses a label-attentive encoder that incorporates label information into the node embedding process, while the student model learns to produce class-friendly node embeddings based on the teacher’s supervision that leads to improved alignment.
2. Related Work
Presented study builds upon several important research areas, including Graph Neural Networks (GNNs), label enhancement methods, and knowledge distillation.
Graph Neural Networks (GNNs)
GNNs have become popular for modeling graph-structured data, with foundational models like Graph Convolutional Networks (GCN) (Kipf and Welling, 2017) and Graph Attention Networks (GAT) (Veličković et al., 2018). While these models perform well for node-level tasks, they often struggle with graph-level tasks like classification, which issue is addressed in this study.
Label Enhancement Methods
Label-enhanced techniques improve model performance by incorporating label information during training. Previous methods focused on various approaches, including:
-
Label-Enhanced Node Embedding (Wang, 2021): Enhances node features by combining them with label information.
-
Label-Enhanced Graph Structure Optimization (Chen et al., 2019): Refines the graph structure itself using label data to improve node propagation.
LAD-GNN builds on these ideas by incorporating label information directly into node embeddings for graph-level tasks, which hadn’t been sufficiently explored in previous work.
Knowledge Distillation
Knowledge distillation, introduced by Hinton et al. (2015), typically uses a large model (teacher) to train a smaller one (student) through soft labels. In GNNs, distillation has been used to reduce model complexity (Yang et al., 2021). LAD-GNN leverages distillation differently, using a label-attentive teacher model to generate ideal embeddings that guide the student model, improving graph classification performance rather than compressing the model.
3. Problem Formulation
Given a graph dataset $D = (G,Y) = \lbrace (G_ {i}, y_ i) \rbrace_ {i=1}^{N}$, where $G_ i \in G$ represents the $i$ -th graph in the dataset and $y_ i \in Y$ is the corresponding graph label, the goal is to learn a low-dimensional graph representation for predicting the graph labels. Each graph $G_ i$ consists of:
- $A_ i \in \mathbb{R}^{n_ i \times n_ i}$ : an adjacency matrix describing the relationships between the nodes in the graph, where $n$ is the number of nodes.
- $X_ i \in \mathbb{R}^{n_ i \times d}$: a node feature matrix where $d$ is the dimension of the node features.
The objective is to learn a function $f$ that maps the graph $G_ i$ to its label $y_ i$ by finding an optimal graph representation.
4. Method
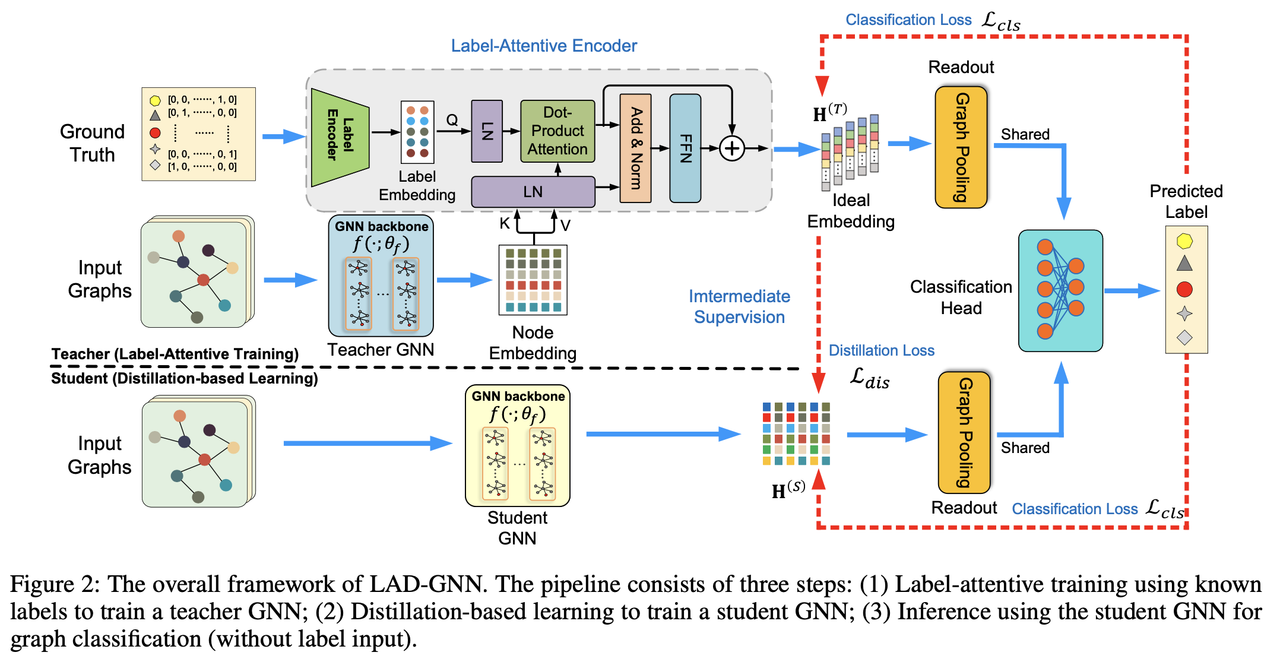 Figure 2. LAD-GNN framework.
Figure 2. LAD-GNN framework.
The proposed LAD-GNN method involves two main stages:
Label-Attentive Teacher Training
The teacher model generates a resulting embedding where both node and label embeddings are fused using an attention mechanism. A label-attentive encoder is employed where graph labels are encoded and combined with node embeddings to form the final embedding used for classification.
Distillation-Based Student Learning
After the teacher model is trained, the student model is trained using a distillation-based approach. The student model learns from the teacher’s ideal embedding through intermediate supervision using both the classification loss and the distillation loss.
Framework of LAD-GNN
GNN Backbone
The GNN backbone forms the core of the LAD-GNN architecture and is responsible for generating the initial node embeddings, which are later refined using the label-attentive encoder. The GNN backbone can be formalized as:
$H_ {v}^{(l+1)} = \text{UPT}\left(H_ {v}^{(l)}, \text{AGG}\left({ H_ {u}^{(l)}\vert u \in N_ v }\right)\right), \forall v \in V$ where $H_ {v}^{(l+1)}$ is the node embedding at layer $l + 1$, $N_ v$ represents the set of neighbors for node $v$, $AGG$ is the aggregation function that combines information from the neighbors, and $UPT$ is the update function applied to node $v$.
After multiple layers of message-passing and aggregation, the final node embeddings $H$ are aggregated into a graph-level representation $Z_ G$ using a readout (pooling) function:
$Z_ G = POOL(\lbrace H_ v\vert v \in V \rbrace)$
where $POOL$ can be an average, max pooling, or an attention-based pooling method. The graph-level representation $Z_ G$ is then passed to the classifier for label prediction:
$\hat{\mathcal{Y}} = g(Z_ G; \phi_ g)$
where $\hat{\mathcal{Y}} \in \mathbb{R}^{N \times c}$ represents the predicted labels with $c$ classes and $\phi_ g$ is the classifier’s parameters.
Label-Attentive Teacher Model
The teacher model integrates label information into the node embeddings through the label-attentive encoder, a critical component of LAD-GNN. The encoder transforms the label $y_ G$ of graph $G$ into a latent embedding using a Multi-Layer Perceptron (MLP): $H_ l = h(y_ G\vert G \in \mathcal{G})$ Where $H_ l$ is the latent label embedding.
This embedding is then combined with the node embeddings $H_ v$ generated by the GNN backbone using a scaled dot-product attention mechanism: $H’_ v = Attention(H_ v, H_ l) = Softmax(\frac{QK^T}{\sqrt{d_ k}} \cdot\tau)V$ where $Q=H_ lW^Q$, $K=H_ vW^K$, and $V=H_ vW^V$ are projections of the label and node embeddings, $d_ k$ is the dimensionality of the projections and $\tau$ is the attention temperature coefficient.
The output $H’_ v$ is normalized using a layer normalization function layernorm (LN), then passed through a feed-forward network (FFN) to generate the final node embedding: $H_ v^{(T)}=FFN(LN(H’_ v + H_ v)) + H’_ v$
The teacher model is optimized using a classification loss:
$\mathcal{L}_ {cls} = \frac{1}{N}\sum_ {i = 1}^{N}{-(y_ {i} \log(\hat{y_ {i}}) + \left( 1 - y_ {i} \right) \log\left( 1 - \hat{y_ {i}} \right))}$
Distillation-Based Student Learning
Once the teacher model is trained, the student model learns to mimic the teacher’s embeddings using a distillation loss aiming to minimize the mean squared error (MSE) between the node embeddings from the teacher and student models:
$\mathcal{L}_ {dis} = \frac{1}{N}\sum_ {i = 1}^{N}{\vert\vert H_ i^{(T)} - H_ i^{(S)}\vert \vert^2_ 2}$
The student model is trained to minimize a combination of the classification loss $L_ {cls}$ and the distillation loss $L_ {dis}$, weighted by a hyperparameter $\lambda$:
$\mathcal{L} = \mathcal{L}_ {cls} + \lambda\cdot\mathcal{L}_ {dis}$
By distilling knowledge from the teacher model, the student GNN can learn to generate class-friendly node embeddings that align better with the graph labels.
The computational complexity of LAD-GNN is comparable to that of traditional GNN backbones, with an added cost for the distillation process. The primary increase in complexity arises from the label-attentive encoder, but this is considered negligible compared to the overall complexity of the GNN model.
 Algorithm of LAD-GNN.
Algorithm of LAD-GNN.
5. Experiments
Datasets
The effectiveness of LAD-GNN is demonstrated through extensive experiments on ten different datasets across multiple domains to ensure a broad understanding of the method’s generalizability. The datasets used in the experiments include:
-
Chemical Datasets: MUTAG, PTC, NCI1, NCI109: These datasets are composed of molecular graphs used for graph classification tasks like predicting chemical compound properties.
-
Bioinformatics Datasets: PROTEINS, ENZYMES: Graphs representing protein structures where the task is to classify proteins or predict enzyme classes.
-
Social Network Datasets: COLLAB, IMDB-BINARY, IMDB-MULTI, REDDIT-BINARY, REDDIT-MULTI-5K: These are graphs representing social networks, where the task is to classify graphs into different social categories or communities.
The experiments are conducted using 7 different GNN backbones: GCN, GAT, GraphSAGE, GIN, DGCNN, SAGPool, and MEWISPool. The performance of LAD-GNN is compared to the base models to measure its effectiveness in improving graph classification accuracy.
Experimental Results
The experiments are evaluated using the standard graph classification metric, accuracy, with the following design considerations:
A ten-fold cross-validation setting is used across all datasets to ensure robust and unbiased results. The datasets are split into train, validation, and test sets with an 80/10/10 split ratio.
Performance Comparison with GNN Backbones The first set of experiments compares the classification accuracy of the baseline GNN models (GCN, GAT, GraphSAGE, GIN, DGCNN, SAGPool, and MEWISPool) with and without the LAD-GNN framework. LAD-GNN consistently improves the performance of all backbones across all datasets. Notable results include:
-
IMDB-BINARY dataset: LAD-GNN achieves a 16.8% improvement in accuracy when combined with the GraphSAGE backbone (from 58.9% to 75.5%).
-
MUTAG dataset: LAD-GNN provides an increase of 4.7% in accuracy on GraphSAGE and similar improvements on other backbones.
-
NCI1 dataset: The performance of GraphSAGE combined with LAD-GNN jumps from 69.9% to 86.7%, representing a significant 16.8% boost.
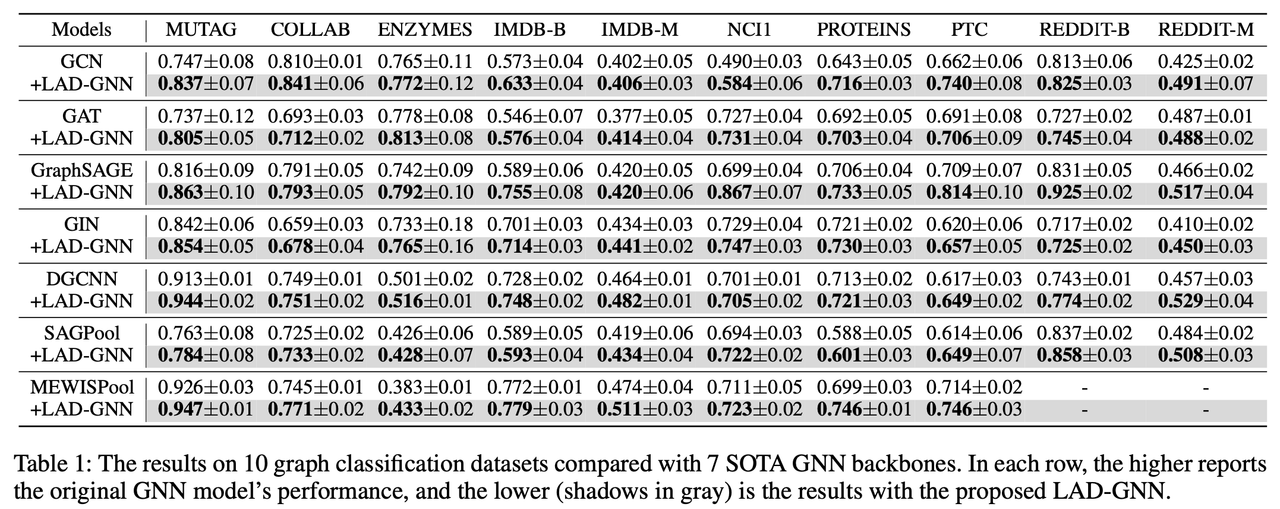 Table 1. Performance comparison of LAD-GNN with GNN Backbones.
Table 1. Performance comparison of LAD-GNN with GNN Backbones.
Comparison with Other GNN Training Methods To further validate the effectiveness of LAD-GNN, the authors compare it with nine other state-of-the-art GNN training strategies, including:
- Manual graph augmentation methods: DropEdge, M-Mixup, and G-Mixup.
- Graph auto-augmentation methods: JOAOv2, AD-GCL, and AutoGCL.
- Graph distillation methods: KD, GFKD, and DFAD-GNN.
Table 2 in the paper shows that LAD-GNN outperforms all these competing methods on most datasets. Specifically:
-
LAD-GNN achieves the highest accuracy on six out of seven datasets, including significant gains on the NCI1, PTC, and PROTEINS datasets.
-
On the MUTAG dataset, LAD-GNN is slightly outperformed by IGSD (Iterative Graph Self-Distillation), though the difference is small. This comparison shows that LAD-GNN is more effective at improving graph classification tasks than other augmentation and distillation-based methods.
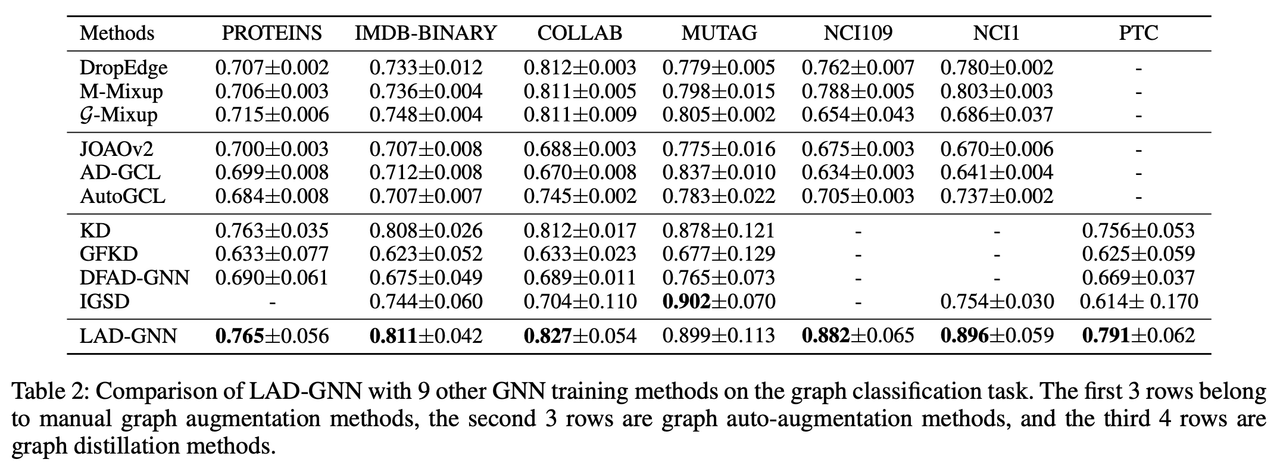 Table 2. Performance comparison of LAD-GNN with with other GNN training tethods.
Table 2. Performance comparison of LAD-GNN with with other GNN training tethods.
To further analyze the performance of LAD-GNN, authors provide Receiver Operating Characteristic (ROC) curves and Area Under the Curve (AUC) values for the MUTAG and PTC datasets. ROC curves are used to visualize the performance of classification models at various threshold settings, and AUC values summarize the model’s ability to discriminate between classes. The ROC curves for LAD-GNN show that it consistently outperforms the baseline GNN backbones (GCN, GAT, GIN, GraphSAGE) on both datasets. Specifically:
-
On the MUTAG dataset, LAD-GNN achieves an AUC of 0.86, which is higher than GCN (0.75), GAT (0.77), and GIN (0.79).
-
On the PTC dataset, LAD-GNN achieves an AUC of 0.80, outperforming GCN (0.71), GAT (0.70), and GraphSAGE (0.76). These results further confirm that LAD-GNN improves the graph classification performance not only in terms of accuracy but also in terms of the overall quality of predictions.
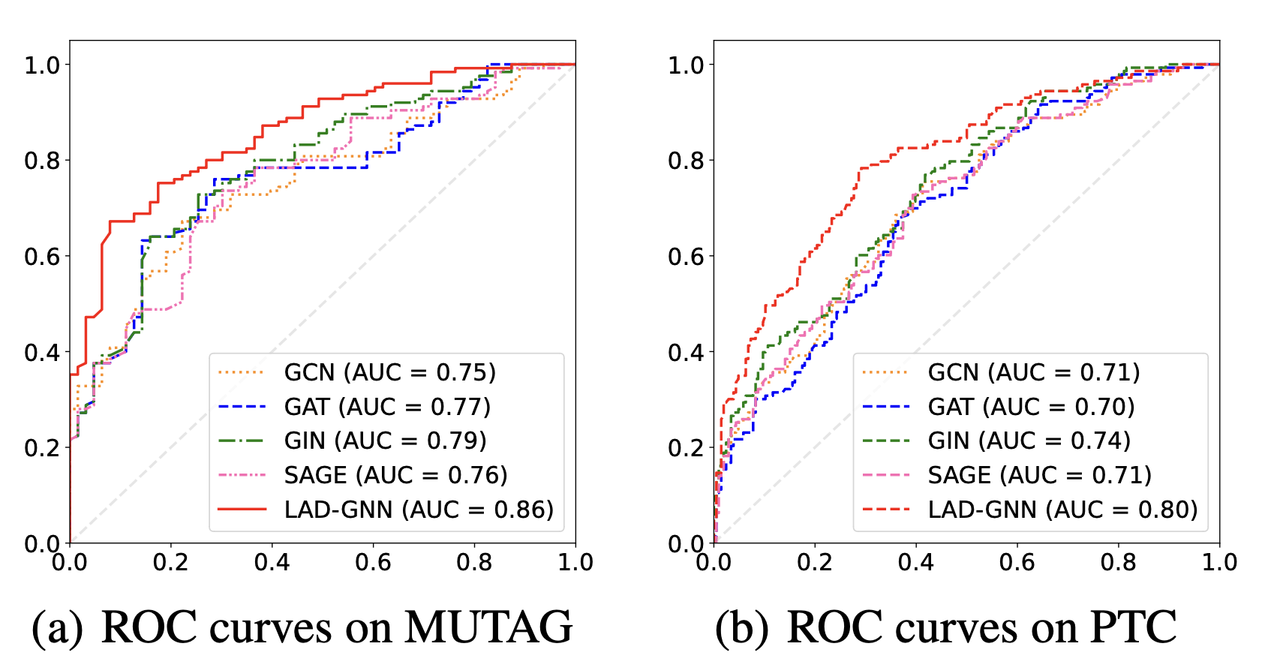 Figure 3. The ROC curves on MUTAG and PTC datasets of GCN, GAT, GIN, SAGE, and the proposed LAD-GNN.
Figure 3. The ROC curves on MUTAG and PTC datasets of GCN, GAT, GIN, SAGE, and the proposed LAD-GNN.
Visualization of Embeddings The t-SNE visualizations of the learned graph embeddings from the original GNN backbones and LAD-GNN are included in the paper. The t-SNE plots reveal that LAD-GNN generates more tightly clustered embeddings, with better separation between classes. This indicates that the label-attentive distillation process helps the model learn more discriminative representations for graph classification tasks. The visualization results are particularly important because they provide an intuitive understanding of how LAD-GNN improves the alignment between node embeddings and graph labels. By incorporating label information into the node embedding process, LAD-GNN produces embeddings that are more class-friendly and easier to separate in the feature space.
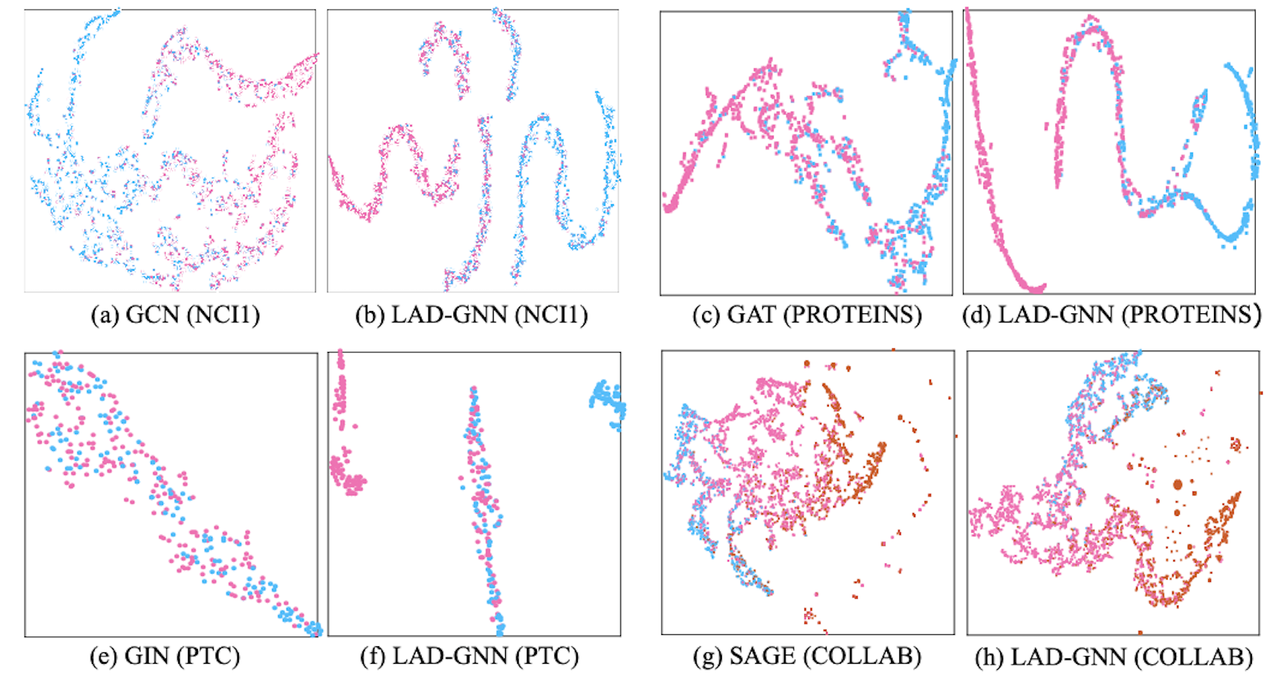 Figure 4: The t-SNE visualization of graph representations for LAD-GNN and the original GNN
Figure 4: The t-SNE visualization of graph representations for LAD-GNN and the original GNN
Hyperparameter Sensitivity The authors analyze the sensitivity of two key hyperparameters:
-
$\lambda$: The weight of the distillation loss in the overall objective function.
-
$\tau$: The attention temperature coefficient in the label-attentive encoder.
The experiments show that the performance of LAD-GNN is sensitive to $\lambda$, with different datasets requiring different values for optimal performance. For example, the best values for $\lambda$ range between 0.1 and 10 depending on the dataset. In contrast, $\tau$ is found to have less impact on the model’s performance, with $\tau = 0.1$ being chosen as a standard value for all datasets. This hyperparameter analysis provides valuable insights into the importance of fine-tuning $\lambda$ for each specific dataset, while keeping $\tau$ relatively stable.
 Figure 5: Hyperparameter sensitivitivity of (a) $\lambda$ and (b) $\tau$ on the 4 datasets
Figure 5: Hyperparameter sensitivitivity of (a) $\lambda$ and (b) $\tau$ on the 4 datasets
6. Conclusion and Key Takeaway
In conclusion, the paper Label Attentive Distillation for GNN-Based Graph Classification offers a significant improvement in graph-level tasks by addressing the embedding misalignment issue present in traditional GNN models. By introducing a novel distillation framework where a teacher model with a label-attentive encoder guides a student GNN, the authors demonstrate substantial improvements in classification accuracy across a wide range of datasets and GNN backbones.
The key takeaway of this study is that introduced LAD-GNN algorithm holds ability to align node embeddings with graph-level labels leads to more discriminative graph representations, improving classification accuracy without substantially increasing computational cost. The method is highly adaptable and versatile and can be integrated with a wide range of GNN backbones. We can say that LAD-GNN as a valuable addition to the GNN ecosystem, offering performance improvements without sacrificing model simplicity or computational efficiency.
Author Information
- Author name: Ignatova Elizaveta
- Affiliation: KAIST Bio and Brain Engineering Department
- Research Topic: Bioinformatic Analysis of Autoimmune Diseases Multi-Omics
References
- Kipf, T. N.; and Welling, M. 2017. Semi-Supervised Classification with Graph Convolutional Networks. In International Conference on Learning Representations (ICLR).
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; and Bengio, Y. 2018. Graph Attention Networks. International Conference on Learning Representations.
- Wang, Y. 2021. Bag of tricks of semi-supervised classification with graph neural networks. arXiv preprint arXiv:2103.13355.
- Chen, D.; Liu, X.; Lin, Y.; Li, P.; Zhou, J.; Su, Q.; and Sun, X. 2019. Highwaygraph: Modelling long-distance node relations for improving general graph neural network. arXiv preprint arXiv:1911.03904.
- Hinton, G.; Vinyals, O.; Dean, J.; et al. 2015. Distill- ing the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2(7).
- Yang, C.; Liu, J.; and Shi, C. 2021. Extract the knowledge of graph neural networks and go beyond it: An effective knowl- edge distillation framework. In Proceedings of the Web Con- ference, 1227–1237.