[NIPS-23] Evaluating Post-hoc Explanations for Graph Neural Networks via Robustness Analysis
Authors: Junfeng Fang, Wei Liu, Yuan Gao, Zemin Liu, An Zhang, Xiang Wang, Xiangnan He
Published in: 37th Con3ference on Neural Information Processing Systems (NeurIPS 2023)
Reviewer: Taewook Ham
0. Preliminaries
Post-hoc based GNN explanation: Graph Neural Network가 graph 혹은 node의 레이블을 예측할 때, 그래프 내의 어떤 요소들(노드 혹은 에지)의 집합이 그 예측값이 나오도록 주요하게 기여했는지를 설명하는 방식이다. GNN이 먼저 예측한 후 이에 기반해 해당 예측을 뒷받침하는 subgraph를 찾기 때문에 post-hoc 방식이라고 부르며, GNN의 예측값의 신뢰성을 위해서 해당 작업은 중요한 일 중의 하나로 여겨진다.
1. Problem Definition
Post-hoc 방식으로 subgraph를 찾은 뒤, 찾은 subgraph가 얼마나 유효한지 확인하기 위해 GNN의 input으로 넣은 뒤 원래의 레이블을 얼마나 잘 예측하는지로 평가한다. 그러나 graph의 일부분에 해당하는 subgraph는 GNN 학습에 사용된 data distribution과 떨어져 있기 때문에 이 subgraph만으로는 충분한 설명력을 얻었다고 보기 어렵다. GNN이 message aggregation을 통해 이용해서 node & structural information을 모아 임베딩을 update하는 원리를 가졌기 때문이다. 이런 현상을 Out-of-Distribution (OOD) 이 발생했다고 하며, 기존의 GNN explanation model들은 OOD 문제를 겪는다. 다시 말해, explanatory subgraph는 일반적으로 전체 그래프와 다른 분포를 가지며, 분포의 차이에서 발생하는 문제를 해결할 새로운 metric이 필요하다.
최근에는 이런 OOD 문제를 해결하기 위해 subgraph 외의 부분(complementary part)을 generation model을 이용해서 그럴듯하게 채워주는 generation-based evaluation이 고안되었다. 그러나 학습된 생성 모델은 필연적으로 bias를 포함하게 되며, 이 bias는 필연적으로 GNN이 consistent한 레이블 예측을 하는 데에 영향을 준다.
2. Motivation
정리하자면, 기존의 removal-based evaluation은 OOD 문제를 해결할 수 없고, generation-based evaluation은 bias가 포함될 위험성이 존재한다. 따라서 논문은 “data distribution과 GNN behavior를 동시에 고려하는 metric을 설계할 수 있을까?”라는 질문을 던지고 이 문제를 해결할 수 있는 OAR (OOD-resistant Adversarial Robustness)이라는 새로운 evaluation framework를 제안한다.
3. Method
지금부터 $\mathcal{G}$의 일부인 explanatory subgraph를 $g_ s$로, 그 여집합(complementary part)을 $g_ {\bar{s}} = g\backslash g_ {s} $로 표기하며, explanation method (explainer)는 $h$를 사용해 $g_ {s} = h(g, f)$로 표기한다.
-
Step 1: Formulation of Adversarial Robustness
이제 adversarial robustness라는 개념을 도입하고 이에 기반하여 새로운 metric에 대한 설명을 하겠다. adversarial robustness of $x$란 모델의 예측을 (잘못된 방향으로) 바꿀 수 있는 최소한의 perturbation으로 정의할 수 있다. 예시를 들기 위해 오리지널 그래프 $\mathcal{G} = (A, X) $와 perturb된 그래프 $\mathcal{G’} = (A’, X’) $로 가정하자. 이때의 $\mathcal{G}$의 GNN explanation $\mathcal{G_ s}$에 가해지는 minimum perturbation $\delta_ {g_ {s}}$를 아래와 같이 정의할 수 있다.
Definition 1.
$ \delta_ {\mathcal{G}_ s} = \min_ {A’} \sum_ {u \in \mathcal{V}} \sum_ {v \in \mathcal{V} \setminus {u}} \left\vert A_ {uv} - A’_ {uv} \right\vert $
$ \text{s.t} \quad \arg\max_ i f(\mathcal{G}’)_ i \neq \arg\max_ i \mathbf{y}_ i, \quad \sum_ {u \in \mathcal{V}_ s} \sum_ {v \in \mathcal{V}_ s \setminus {u}} \left\vert A_ {uv} - A’_ {uv} \right\vert = 0, $
$\text{where}$ $V$ and $V_ s$ are the node sets of $\mathcal{G}$ and $\mathcal{G_ s}$, respectively.
식을 정리해보자면, 원래의 adj matrix $A$와 perturb된 adj matrix $A’$을 element-wise하게 뺄셈을 했을 때, 그 차이를 가장 적게 하는 perturbation을 구하는 것이다. 이때 perturb를 하더라도 원래 그래프의 subgraph는 보존되어야 하며, 원래의 레이블과 perturbation 그래프를 통한 예측값은 달라야 한다. 그리고 우리는 이 minimum perturbation 값이 클수록 high adversarial robustness $\delta$를 지니고 있다고 이해할 수 있다. Definition 1을 통해 subgraph $\mathcal{G_ s}$가 잘 뽑혀있을수록 wrong prediction으로 유도하기 위한 complementary part에 대한 perturbation이 어려워진다고 생각할 수 있다(= perturbation 횟수가 늘어날 것이다). 즉, label-irrelevant한 $g_ {\bar{s}}$를 바꿈으로써 prediction을 바꾸기는 쉽지 않아야 한다.
그러나 이 식을 우리의 feasible metric으로서 직접 사용하기에는 몇 가지 문제점이 있다. 첫 번째 문제는 식이 tractable 하지 않다는 점이고, 두 번째 문제는 이 metric이 data distribution을 반영하는지 알 수 없다는 점이다.
-
Step 2: Finding a Tractable Objective
위에서 논의한 사실에 기반하여 Proposition 1을 아래와 같이 제시한다.
Proposition 1: $\mathcal{G}$를 잘 설명하는 explanation $\mathcal{G_ s}$가 고정되어 있다면, 그 complementary part인 $\mathcal{G_ {\bar{s}}}$를 perturb하는 것은 모델 예측에 미미한 영향을 끼친다.
그리고 기존의 Definition 1을 tractable하게 수정하여 Definition 2를 제시한다.
Definition 2
$ \delta^{*}_ {\mathcal{G}_ s} = \mathbb{E}_ {\mathcal{G}’} \left( f(\mathcal{G}’)_ c - \mathbf{y}_ c \right) $
$ \text{s.t} \quad c = \arg\max_ i \mathbf{y}_ i, \quad \sum_ {u \in \mathcal{V}_ s} \sum_ {v \in \mathcal{V}_ s \setminus {u}} \left\vert A_ {uv} - A’_ {uv} \right\vert = 0, $
perturb된 그래프 $\mathcal{G’}$를 GNN에 넣었을 때 label prediction 값의 차이의 기대값을 adversarial robustness로서 정의함으로써 tractable한 function으로 수정된 것을 확인할 수 있다. 이때 당연히 subgraph는 perturb가 되더라도 보존되어야 한다.
자, 그렇다면 남은 것은 앞서 언급된 evaluation process가 data distribution을 반영할 수 있도록 만드는 것이다. -
Step 3
우리는 OOD reweighting block이라는 요소를 도입해서 두 번째 문제를 해결하고자 한다. OOD reweighting block을 통해서 생성된 각 그래프 $\mathcal{G’}$이 얼마나 train dataset의 분포로부터 떨어져 있는지에 대한 OOD score를 계산한다. 이때 그래프를 생성할 때는 학습된 VGAE(Variational Graph Auto-Encoder)를 통해 $\mathcal{G’}$를 생성한다. VGAE는 일반적인 VAE처럼 인코더와 디코더로 구성되어 있고, prior를 gaussian으로 가정하거나, reparametrization trick을 사용하는 등 전반적인 기저 원리는 서로 유사하다. 인코더와 디코더에 대한 구체적인 설명은 생략하고 관계식으로만 대체하겠다.
-
Encoder:
$ q(\mathbf{Z} \vert \mathbf{A’}, \mathbf{X’}) = \prod_ {i=1}^{\vert\mathcal{V}’\vert} q(z_ i \vert \mathbf{A’}, \mathbf{X’}) = \prod_ {i=1}^{\vert\mathcal{V}’\vert} \mathcal{N}(z_ i \vert \mathbf{\mu}_ i, \text{diag}(\mathbf{\sigma}_ i^2)), $
-
Decoder
$ p(\mathbf{A’} \vert \mathbf{Z}) = \prod_ {i=1}^{\vert\mathcal{V}’\vert} \prod_ {j=1}^{\vert\mathcal{V}’\vert} p(A’_ {ij} \vert \mathbf{z}_ i, \mathbf{z}_ j), $
$ \text{with} \quad p(A’_ {ij} = 1 \vert \mathbf{z}_ i, \mathbf{z}_ j) = \sigma(\mathbf{z}_ i^\top \mathbf{z}_ j), $
-
OOD score
$ \mathcal{L}_ {\text{recon}}(\mathcal{G}’) = -\log p(A’ \vert \mathbf{Z}), \quad \text{with} \quad \mathbf{Z} = \mu = \text{GCN}_ \mu (A’, X’). $
OOD score는 위의 식처럼 $\mathcal{L}_ {\text{recon}}(\mathcal{G}’)$ , 즉 NLL(negative log likelihood)의 역수를 취함으로써 얻을 수 있다(($p(A’ \vert \mathbf{Z})$)는 디코더의 output). 더 직관적으로 이해를 해보자면, 학습 데이터 셋의 분포로부터 많이 벗어난 $\mathcal{G’}$은 높은 Loss를 받을 것이고, 그 역수를 취한다면 할당되는 OOD score는 낮아진다. 그 반대의 경우로, 학습 데이터 셋의 분포와 가깝다면 동일하게 계산해 높은 OOD score를 받을 것이고, 결과적으로 합리적인 evaluation metric을 얻을 수 있다.
-
Overall evaluation process
-
Subgraph $\mathcal{G_ s}$를 평가하기 전에 OOD reweighting block (VGAE)을 데이터셋 D에서 샘플된 input graph G를 사용하여 학습시킨다.
-
이후 $\mathcal{G_ s}$를 고정한 상태에서 $\mathcal{G_ {\bar{s}}}$의 구조를 무작위로 변형하여 G′를 생성한다.
-
각 $\mathcal{G’}$는 GNN f와 VGAE에 동시에 입력되어 예측 결과와 OOD 점수를 평가하며, 이 과정에서는 GNN의 동작과 데이터 분포를 모두 고려한다.
-
마지막으로 예측 결과와 OOD 점수를 기반으로 생성된 그래프들의 예측값에 가중치를 부여하여 가중 평균을 계산한다. 이 가중 평균이 원래 그래프 G의 예측값에 가까울수록 설명 그래프 $\mathcal{G_ s}$의 품질이 높다고 평가한다.
-
-
-
SimOAR(Simplified version of OAR)
OAR은 VGAE를 학습시키기 위해서 시간이 오래 걸리고, OOD score가 edge deletion 개수에 크게 영향을 받는 단점이 있다. 일반적으로 같은 횟수의 perturbation을 받은 두 그래프가 있다면, 각각에 할당되는 OOD score는 비슷한 경향이 있다는 사실을 이용해서 단점을 보완한 SimOAR framework를 제시한다.
SimOAR은 계산을 줄이기 위해서 OOD reweighting block을 비활성화하고, 그래프의 원래 엣지 수에 대한 perturbation 비율을 미리 정의된 값으로 제한한다. 그 후, 이를 통해 생성된 그래프들의 평균 예측값을 계산하여 예측을 근사한다. SimOAR로 생성된 몇몇 그래프가 분포를 벗어날 가능성은 있지만, 그럼에도 불구하고 SimOAR은 일관성과 성능 면에서 기존 metric보다 뛰어난 성능을 보인다.
4. Experiments
실험은 크게 세 가지 질문에 답을 하기 위한 목적으로 진행되었다.
RQ1. OAR과 SimOAR이 기존 evaluation 방식들에 비해서 얼마나 evaluation을 잘 할 수 있는 metric인가?
RQ2. OAR과 SimOAR이 기존 evaluation 방식들에 비해서 더 일반화할 수 있는 metric인가?
RQ3. evaluation 과정에서 OOD reweighting block의 impact는 무엇인가?
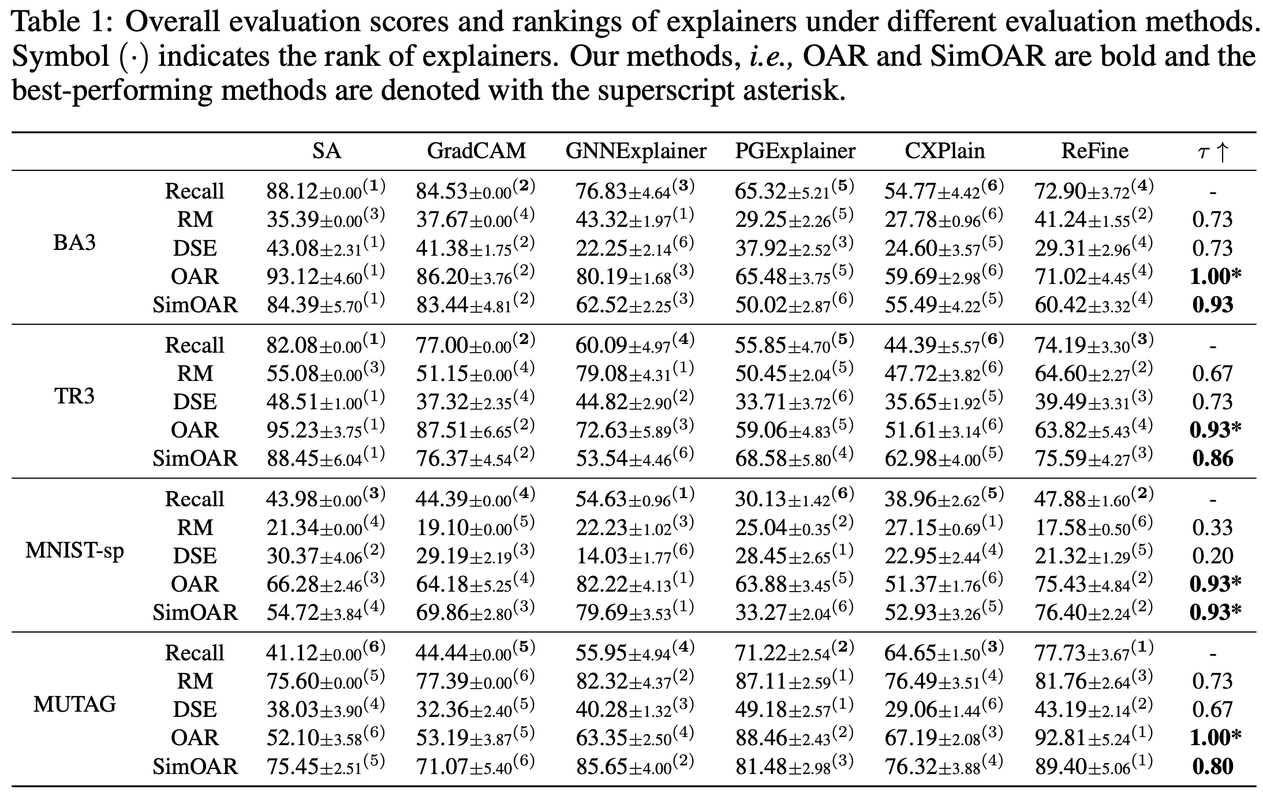
BA3, TR3, Mutagenicity, MNIST-sp와 같은 다양한 데이터셋에서 실험이 진행되었으며, 사용할 explainer model 들은 SA, GradCAM, GNNExplainer, PGExplainer, CXPlain,ReFine 이다. baseline이 되는 metric들은 Recall, removal-based evaluation, generation-based evaluation 로 삼았다. 아래 table에서 확인 가능하듯, OAR과 SimOAR은 기존 메트릭에 비해 일관된 성능 향상을 보여주었다. 특히, SimOAR은 계산 속도를 크게 향상시키면서도 높은 성능을 유지했다.
RQ1: How is the evaluation quality of OAR and SimOAR compared to that of existing metrics?
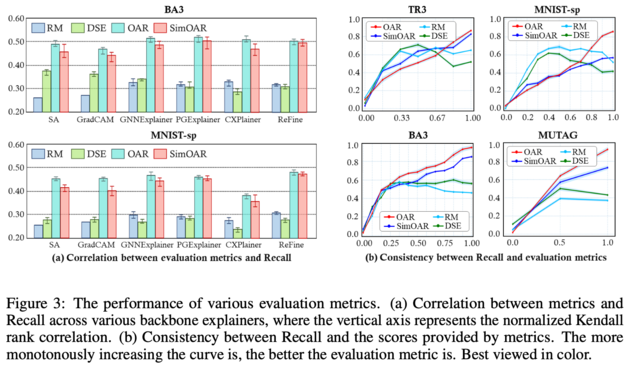
첫 번째 질문에 대한 답으로서 paper에서는 새롭게 제시한 metric이 기존의 Recall과 얼마나 consistency를 가지는지 확인했다. 각 explainer별 수치를 줄세우기 했을 때 아래와 같이 정의된 consistency $\tau$의 수치를 확인해보았다. $\tau$ 값이 높을수록 explainer별로 metric value 크기 순서가 Recall과 일치한다고 이해할 수 있다. 아래의 Table 1과 Figure 3(a)를 통해서 우리는 OAR이 removal-based (RM)나 generation-based (DSE) 방식보다 Recall과 더 유사하다는 것을 확인했다. 추가로, SimOAR이 OAR에 비하여 성능 면에 있어 크게 뒤떨어지지 않는다는 것을 알 수 있다.
$ \tau \left( {r^i}_ {i=1}^n, {s^i}_ {i=1}^n \right) = \frac{2}{n(n+1)} \sum_{i < j} I \left( \text{sgn}(r^i - r^j) = \text{sgn}(s^i - s^j) \right), $
RQ2: How is the generalization of OAR and SimOAR compared to that of existing metrics?
paper에서는 두번째 논의로 OAR과 SimOAR 방식의 일반화 가능성에 대한 분석을 제시한다. 실험적으로 특정 explainer는 특정 패턴을 선호하는 경향이 있으며, 이러한 explainer가 추출하는 subgraph가 유사한 구조를 가지는 경우가 빈번하다. 따라서 특정 explainer를 바탕으로 한 실험 결과가 다른 기존의 혹은 앞으로의 explainer들에 대해 잘 일반화되지 않을 수 있다는 점을 지적하고 있다. 따라서 우리는 fake subgraph를 샘플링하여 일반화된 evaluation scenario를 시뮬레이션 한다. 이는 explainer들이 가진 bias의 한계를 피하고 전체 그래프에서 무작위로 샘플링된 서브그래프들을 사용함으로써 평가를 수행하는 방법이다. 이 방법은 다양한 explainer들에 대해 평가 점수와 Recall 수준 간의 일관성을 높이는 데 중점을 두고 있다.
Figure 3(b)는 모든 evaluation methods에 대한 평균 정규화 점수를 의미한다. 그리고 가장 이상적인 경우는 evaluation score가 Recall level에 대해 monotonic하게 증가하는 경우이다. 실험 결과, Figure 3(b)에서 볼 수 있듯, OAR과 SimOAR 방법이 다양한 explainer에서 evaluation scores와 Recall의 일관성을 높인다는 것을 볼 수 있으며, 이는 이 방법이 다른 설명자들에 대해서도 우수한 성능을 발휘할 가능성이 크다는 것을 시사한다.
RQ3: What is the impact of the designs (e.g., the OOD reweighting block) on the evaluations?
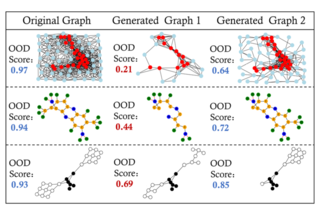
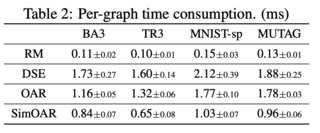
앞선 Table 1에서 확인할 수 있듯, OAR과 SimOAR 간의 성능 차이가 발생하는 것으로, OOD reweighting block의 영향력을 알 수 있으며 OOD score를 0부터 1까지 정규화 가능하다는 점에 기여했다는 사실도 알 수 있다. 또한 아래의 Figure 4에서 OOD block이 전체 그래프의 underlying property를 벗어난 생성그래프에 대해서 낮은 점수를 부여할 수 있다는 점을 명시적으로 확인할 수 있다. 다만 앞서 언급했듯, OOD block을 학습시키는 과정은 꽤나 time-cost한 일이다. Table 2를 통해 OAR과 SimOAR이 소모하는 시간까지 비교할 수 있다.
5. Conclusion
이 논문은 GNN explanation evaluation에서 OOD 문제를 해결하는 새로운 metric을 제시한다. OAR은 adversarial robustenss을 기반으로 explanatory subgraph의 신뢰성을 평가하며, 데이터 분포를 고려하는 OOD reweighting을 통해 정확한 평가를 제공한다. 실험 결과, OAR과 SimOAR은 기존 메트릭에 비해 우수한 성능을 보여주었으며, 이는 향후 GNN explainability 연구에 중요한 기여를 할 것이다.
6. References
Fang, Junfeng, et al. “Evaluating post-hoc explanations for graph neural networks via robustness analysis.” Advances in Neural Information Processing Systems 36 (2024).