[CVPR-2023] Deep Graph Reprogramming
1. Introduction
Graph data의 폭발적인 증가에 따라 GNN은 추천 시스템, 자율 주행 등 다양한 분야에서 사용할 수 있게 되었습니다. 하지만 막대한 training effort와 메모리 문제에 의해 한정된 자원으로 GNN을 활용하는 것에 있어 한계가 있습니다. 이를 해결하기 위해 최근 pre-trained GNNs을 재사용 함으로써 training cost를 감소시키려는 연구가 활발하게 진행되고 있습니다.
대표적으로 non-Euclidean domain에서의 knowledge distillation이 있지만, 이는 per-task-per-distillation으로 각 작업마다 별도의 distillation 모델이 필요하기에 여러 작업을 처리할 때 저장 및 계산 측면에서 부담이 존재합니다.
또한, 사전 훈련된 모델이 충분한 Euclidean domain과는 달리, graph와 같은 non-Euclidean domain에서는 다음과 같은 문제점이 있습니다:
- Input 측면
- 다양한 feature 차원을 가진 불규칙한 그래프
- Task 측면
- 다양한 task-level(graph-, node-, edge-) 및 settings(transductive, inductive)과 같은 구조적 다양성
위 두 가지 이유로 인해, downstream task를 진행하기 위한 적합한 pre-trained된 GNN 모델이 충분하지 않다는 문제점이 있습니다.
본 논문은 Graph Neural Networks (GNNs)를 위한 novel reusing task인 Deep Graph Reprogramming에 대한 연구를 소개하고 있습니다. Pre-trained된 GNN model에 대해, raw node feature 혹은 model parameter를 tuning 하지 않고 다양한 domain의 cross-level downstream task들을 해결하는 것을 목표로 하고 있습니다.
다양한 cross-level downstream task를 해결하기 위하여 두 가지 paradigm을 제안합니다.
- Data Reprogramming Paradigm (DARE)
- Input 측면에서 여러 task에 따른 다양한 graph feature 차원의 문제점을 해결할 수 있습니다.
- Model Reprogramming Paradigm (MERE)
- Model 측면에서, fixed per-task-per-model behaviour, 즉 특정 task를 해결하기 위해 각 task에 맞는 별도의 모델이 필요한 문제점을 완화할 수 있습니다.
Data 측면의 paradigm인 DARE와 model 측면의 MERE는 각각 다른 setting을 고려하여 다음과 같은 세부 사항으로 나뉩니다.
1. Data Reprogramming (DARE)
- Reprogramming in heterogenous-domains
- Meta-FeatPadding (MetaFP)
- Reprogramming in homogenous-domains
- Edge-Slimming (EdgSlim)
- Meta-GraPadding (MetaGP)
2. Model Reprogramming (MERE)
- Reprogrammable Aggregating (ReAgg)
Meta-FeatPadding approach를 통해 이질적(heterogenous) 차원을 가진 graph를 pre-trained GNN model로 padding을 통해 작은 변형을 가해 reusing을 가능하게 합니다. Edge-slimming과 Meta-GraPadding은 동질적(homogenous) 차원을 가진 graph를 각각 edge 제거와 작은 graph를 추가하는 방식을 통해 처리할 수 있습니다.
모델 측면에서의 Reprogrammable Aggregating 방법은 Gumbel-Max trick을 기반으로 pre-trained model의 aggregation behaviour를 변형시켜 다양한 downstream task를 해결할 수 있습니다.
이처럼 본 논문은 위 세 가지 approach를 통해, re-training 혹은 fine-tuning 없이도 pre-trained GNN model을 이용해 다양한 domain에서의 cross-level downstream task를 진행할 수 있게 하는 reusing paradigm을 제안하고 있습니다.
2. Background
2.1. Model Reusing
GNN model reusing은 [1] 에서 pre-trained model을 경량화된 GNN model로 변환하기 위해 GNN에 특화된 knowledge distillation(KD) 방법을 제안함으로써 처음 알려지게 되었습니다. 이후 이 연구를 토대로, graph가 없는 환경에서의 KD 등 다양한 setting에서 도전적인 연구들이 활발하게 진행되고 있습니다.
Pre-trained된 GNN model을 reusing하는 3가지 주된 요인은 다음과 같습니다.
- Enhance performance
- Reduce training efforts
- Improve inference speed
위 3가지 목적을 달성하기 위해 여러 연구들이 제안되고 있지만, 현재까지 주로 사용되고 있는 방법은 distillation-based method들로, 무거운 teacher model로부터 핵심 knowledge를 추출하여 작고 가벼운 student model이 학습할 수 있도록 하는 기법을 의미합니다. 이를 통해 student model은 teacher model의 복잡한 구조를 유지하지 않으면서도 유사한 성능을 낼 수 있도록 합니다.
본 논문은 이러한 전통적인 기법 및 이전 연구들과는 달리 병렬적으로 처리하는 GARE-based method를 소개하고 있습니다.
2.2. Knowledge Distillation
앞서 이야기했듯이, Knowledge Distillation은 teacher model로부터 지식을 추출하고 전달하여, 가벼운 student model을 처음부터 재훈련시키는 것입니다. 이 방식에는 크게 2가지 문제점 및 한계점이 존재합니다.
- Knowledge distillation은 이상적인 조건에 의존하고 있습니다.
- Image, 즉 Euclidean domain의 data 경우, ImageNet과 같은 대규모 데이터셋에서 훈련된 model이 downstream task에 사용될 수 있습니다.
- 하지만 graph와 같은 non-Euclidean domain의 data일 경우, 다양한 input dimension과 feature type 등 다양한 구조적인 측면을 고려한 충분한 pre-trained model이 없기에 KD 방법을 사용하기에는 한계점이 있습니다.
- Knowledge distillation은 resource 측면에서 비효율적입니다.
- Knowledge distillation을 통해 추출된 student model은 teacher model과 정확히 동일한 task들만 처리할 수 있고, 특정 작업에만 사용되기에 multi-task scenario에서 모델이 중복될 수 있습니다.
이처럼 Knowledge distillation과 달리 논문에서 제안하는 GARE method는 하나의 pre-trained model을 통해 다양한 domain과 cross-level task를 re-training 혹은 fine-tuning 없이 진행할 수 있으며, 메모리 측면에서도 효율적입니다.
2.3. Adversarial Reprogramming
Adversarial reprogramming은 target model에 작은 변형을 가하여 공격자가 목적을 바꾼 task를 수행하도록 하는 적대적 공격의 유형입니다. 본 논문에서는 graph에 적대적 변형을 가하여 GNN이 공격자가 선택한 task를 수행하도록 재목적화하는 것을 의미합니다. Adversarial reprogramming은 image classification [2, 3] 및 language understanding [4] 등 다양한 분야에서 연구되고 있지만, non-Euclidean domain에서의 연구는 아직 진행되지 않았습니다. 저자들이 제안하는 deep graph reprogramming이라는 용어는 adversarial reprogramming으로부터 유래되었으며, 이는 GNN에서 adversarial reprogramming을 탐구한 첫 번째 연구로, 이 방식을 통해 효율적인 model reusing의 방법을 제시하고 있습니다.
Adversarial reprogramming은 여러 task level에 따라 분류할 수 있으며, 대표적으로 다음과 같은 유형들이 있습니다.
- Adversarial node-level perturbation [5]
- 공격자가 node를 추가 및 제거하거나, target node의 feature를 변형하여 공격하는 것을 의미합니다.
- Adversarial edge-level perturbation [5]
- 공격자가 edge를 추가 및 제거하거나, 다르게 연결함으로써 공격하는 것을 의미합니다.
- Adversarial structure-level perturbation [5]
- Edge-level perturbation과 동일하게 edge를 수정하지만, degree의 총합이나 node distribution과 같은 structure information을 보존하는 것을 전제로 하고 있습니다.
2.4. Gumbel-Max trick
Gumbel-Max trick [6,7] 은 sampling을 위한 간단한 방법으로, 주어진 복잡한 확률 분포에서 sampling하기 위해 사용됩니다. 즉 Gumbel(0,1) 분포로부터 random 값을 추출하여 log로 표현된 확률값에 Gumbel noise 값을 더해주고, 이 과정에서 가장 큰 값을 갖는 범주를 선택하게 됩니다. 수식으로 표현하면 다음과 같습니다.
$X = \arg\max_{k \in {1, \dots, K}} (\log \alpha_k + G_k), \quad \text{where } G_1, \dots, G_k \, \text{i.i.d.} \sim \text{Gumbel}(0, 1)$
Gumbel-Max trick은 argmax function에 의존하기 때문에 non-differentiable 합니다. 이를 해결하기 위해 Gumbel-softmax가 나오게 되는데, 이는 연속적인 확률 분포로부터 sample을 뽑는 방법으로 argmax function을 softmax function으로 대체하여 나타내었고, differentiable 합니다.
$\hat{X}_k = \text{softmax} \left( \frac{\log \alpha_k + G_k}{\tau} \right), \quad \text{where } G_1, \dots, G_k \, \text{i.i.d.} \sim \text{Gumbel}(0, 1)$
수식에서 타우는 temperature를 나타내며, softmax의 출력을 조절하는 중요한 parameter입니다. 이는 sampling의 sharpness와 분산을 결정합니다. 타우가 0에 가까워질수록 argmax function에 가까워지는 반면, temperature가 infinity로 갈수록 uniform distribution에 가까워지는데, 이는 noise의 상대적인 차이가 감소하면서 모든 선택에 대한 확률이 균등하게 분포되기 때문입니다.
3. Proposed Methods
3.1. Data Reprogramming (DARE)
Input 측면에서 graph의 다양한 feature 특징을 해결하기 위하여, graph 표현을 재구성하여 다양한 downstream task의 특징에 따라 pre-trained GNN을 맞추는 작업이 필요합니다. CNN domain에서 사용되던 adversarial reprogramming에 영감을 받아, pre-trained된 GNN에도 적용하여, domain에 상당한 차이가 있는 보지 못한 새로운 task를 해결하는데 reusing을 할 수 있도록 합니다.
3.1.1. Meta-FeatPadding (MetaFP)
Meta-Feat Padding(MetaFP)은 raw features 주위에 padding을 함으로써 다양한 downstream dimension을 다룰 수 있게 하는 것을 목표로 하고 있고, 이는 노드 레벨 [5] 의 adversarial perturbation을 기반으로 하고 있습니다. 즉 MetaFP는 heterogenous dimension을 해결하기 위한 method로 볼 수 있습니다. 다음은 padding feature를 만드는 수식인데, (x,y)는 각각 downstream graph feature와 대응되는 label이며, 이들은 downstream data distribution을 따릅니다.
$\min_ {\delta_ {\text{padding}}} \, \mathbb{E}_ {(x, y) \sim \mathcal{D}} \left[ \mathcal{L}_ {\text{downstream}} \left( \text{GNN}_ {\text{pre-trained}} \left[ x \parallel \delta_ {\text{padding}} \right], y \right) \right]$
Raw input feature인 x와 optimised padding feature를 concat하여 feature padding을 수행하고, label y와 비교하며 loss를 minimise함으로써 학습하게 됩니다. 즉 downstream task의 feature dimension을 pre-trained GNN model과 일치시킬 뿐만 아니라 loss function을 동시에 minimise 하기에, downstream performance를 향상시킬 수 있습니다. 참고로 저자는 optimised padding을 생성하는데까지 하나 혹은 몇 개의 epoch만이 필요하다고 하고 있습니다.
3.1.2. Edge-Slimming (EdgSlim)
Edge-slimming 같은 경우, 엣지 레벨 [5] 의 adversarial perturbation을 기반으로 heterogenous(이질적인) 차원을 고려할 필요가 없을 때, homogenous(동질적인) 차원에서 접근하는 방식을 제안하는 방법입니다. 노드 수준의 방해 요소에서 벗어나, downstream graph data에서 raw node feature를 변경하지 않고 노드 연결을 수정함으로써 resource 측면에서의 효율적인 model reusing을 달성하는 것을 목표로 하고 있습니다. 다음 수식은 EdgSlim의 알고리즘 과정인데, 이를 최적화함으로써 downstream task의 손실을 줄일 수 있습니다.
$\min_ {{u_i, v_i}_ {i=1}^m} \sum_ {i=1}^{m} \left\vert \frac{\partial \mathcal{L}_ {\text{downstream}}}{\partial \alpha_ {u_i, v_i}} \right\vert$
s.t : $\widetilde{\mathcal{G}} = \text{Modify} \left( \mathcal{G}, {\alpha_ {u_ i, v_ i}}_ {i=1}^m \right)$ $= \left( \mathcal{G} \setminus {u_ i, v_ i} \right), \text{if} \, \frac{\partial \mathcal{L}_ {\text{downstream}}}{\partial \alpha_ {u_ i, v_ i}} > 0$
위 loss function을 $\alpha_{u_i, v_i}$ 에 대해 미분을 하는데 이는 edge gradient를 나타내며, 이때 0보다 큰 downstream graph에 있는 edge를 순차적으로 큰 순서대로 제거하게 됩니다. 단순히 불필요한 edge를 제거하는 것만으로도 downstream loss를 최소화할 수 있습니다. 또한 학습 속도 향상, 모델의 간소화 그리고 과적합 방지를 가능하게 하고, 반대로 0보다 작은 기울기를 제거하면 안 되는 이유는 noise나 모델을 향상시키기 위한 정보들을 놓칠 수 있기 때문입니다. EdgSlim 최적화 과정 또한 빠르게 수렴하기에 resource 측면에서 효율적이라고 볼 수 있습니다.
3.1.3. Meta-GraPadding (MetaGP)
Meta-GraPadding approach는 EdgSlim의 만족스러운 결과에도 inductive setting에서는 적용할 수 없다는 문제점을 해결하기 위해 structure-level [5] 의 adversarial perturbation 기반으로 제안하는 방법입니다. 즉 raw node feature 주위에 padding하는 대신, 작은 subgraph를 생성하고 downstream graph 주위에 padding을 시켜주는 방식입니다. subgraph는 10개 정도의 작은 갯수의 노드로 이루어져 있고, meta node 경우 fully connected 방식으로, 모든 downstream node와 연결되게 합니다. 추론 단계에서 training된 subgraph가 test graph에 padding되어, pre-trained GNN을 통해 downstream inductive task를 수행할 수 있게 해줍니다.
3.2. Model Reprogramming (MERE)
DARE의 접근 방식으로도 충분한 performance를 얻을 수 있지만, pre-trained task와 domain 측면에서 차이가 심한 경우 성능이 떨어지는 경우를 볼 수 있습니다. 이는 GNN의 parameter와 architecture가 고정되어 있기에 발생하는 문제로 추론을 하였고, 이를 해결하고자 GNN의 가장 중요한 특성인 message aggregation을 고려하는 MERE 방식을 제안하였습니다.
3.2.1 Reprogrammable aggregating (ReAgg)
Reprogrammable aggregating(ReAgg)은 모델 측면에서 DARE approach를 보완하는 방식으로, domain gap 차이가 큰 시나리오에서의 문제를 해결하기 위해 제안되었습니다. ReAgg 방식은 모델의 parameter를 바꾸지 않고, 다양한 downstream task에 대해 aggregating behaviour를 dynamic하게 바꾸어주는 것을 목표로 하고 있습니다. 여기서 미분이 불가능한 결정 방식이라는 문제가 있는데, 이를 해결하는 방법으로는 강화학습 혹은 SemHash technique [8] 을 도입하는 방법이 있습니다. 하지만 강화학습 같은 경우, Monte Carlo search process에 의한 computation cost가 높다는 단점이 있고, SemHash 경우, 특정 aggregator가 항상 선택되거나, 아예 선택되지 않는 collapse 문제가 생긴다는 문제점이 있습니다. 이에 저자들은 앞서 설명한 Gumbel-Max trick의 softmax function으로 대체한 미분가능한 Gumbel-Softmax estimator를 통해 이 문제점을 해결하고자 하였습니다. 다음은 Gumbel-Softmax estimator를 이용한 각 downstream task에 대해 최적의 aggregator를 선택하는 방식을 나타낸 것입니다.
$\text{Aggregator}_k = \text{softmax} \left( \frac{\mathcal{F}(G) + G}{\tau} \right)$
k는 k번째 downstream task를 의미하고, G는 Gumbel random noise로 모델의 붕괴 문제를 해결하여 줍니다. 이로써 ReAgg approach를 통해 domain 차이가 큰 경우에도 최적의 aggregation behaviour를 결정하여 모델의 성능을 보완 및 향상시켜줄 수 있습니다.
4. Experiments
실험을 각각 살펴보기 앞서, 저자들은 진행되는 실험에 대해 State-Of-The-Art 성능을 달성하는 것이 목표가 아닌 한정된 계산 및 컨디션에서 최대한 다양한 downstream task에서 우수한 성능을 도출해 내는 것이 목표 라고 말하고 있습니다. 14개의 공개된 benchmarks를 소개하였는데, 세부사항은 다음과 같습니다.
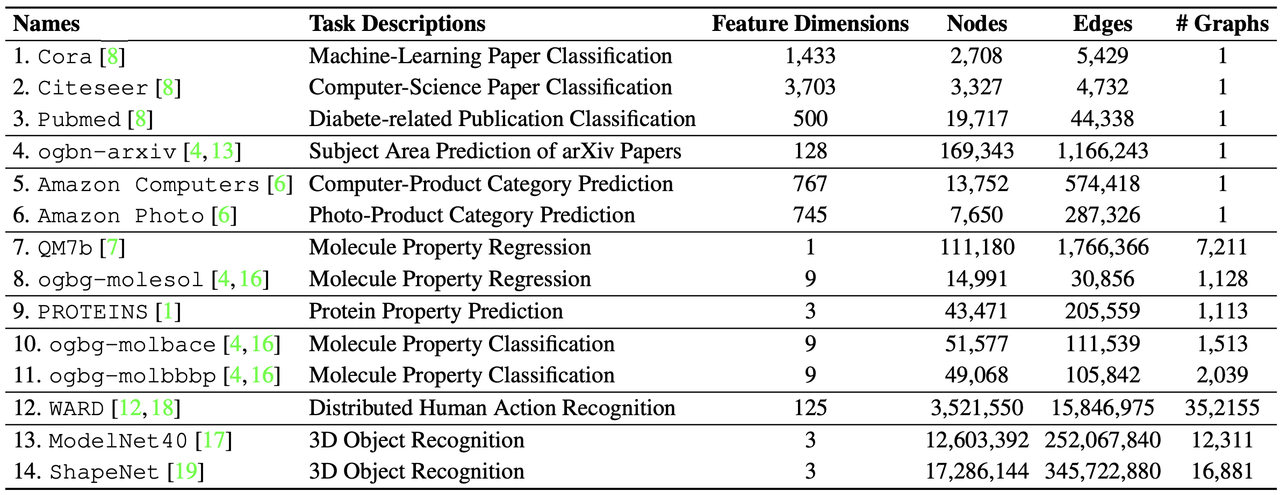
Table 1
또한 모든 실험은 NVIDIA GeForce RTX 2080 Ti GPU 한대를 사용하여 수행하고 있습니다.
저자들은 실험을 크게 2가지, 즉 이질적인(Heterogenous) domain과 동질적인(Homogenous) domain으로 나누어 진행하였습니다.
4.1. Heterogenous - Domains
첫번째는 node classification task에 대한 결과입니다.

Table 2
본 실험은 Citeseer dataset으로 사전 훈련을 하고, 다양한 heterogenous dimension을 가진 데이터셋에 대해 사전 훈련된 모델을 적용한 결과입니다. MetaFP는 모델을 retraining을 하지 않고 진행하였기 때문에, retraining을 한 모델들보다 성능이 살짝 못미치지만 비교할 수 있을 만한 성능을 보여주고 있습니다. 특히 MERE의 ReAgg approach를 더해준 결과, MetaFP만을 사용한 결과보다 평균적으로 2.3% 향상된 모습을 보여주고 있습니다. Cora 데이터셋 같은 경우 ReAgg 방법을 사용했을 시 결과가 조금 하락하는 것을 볼 수 있는데, 이는 Citseer와 Cora 데이터셋이 모두 computer science domain의 데이터 셋으로 domain 차이가 나지 않아 ReAgg 방법이 효과적이지 않는 것을 볼 수 있습니다.
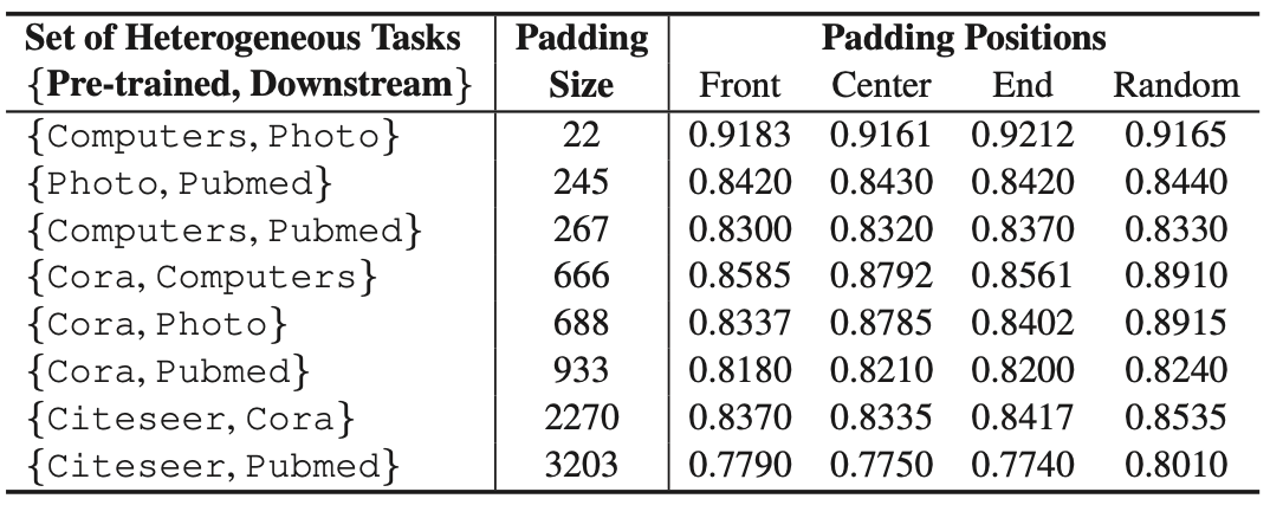
Table 3
Table 3 는 padding size와 padding하는 위치에 변화를 주고, 다양한 pre-trained task와 downstream task에 MetaFP를 적용하여 성능을 비교한 결과입니다. 여기서 주목할 만한 점은 작은 padding size와 random한 position에 padding을 진행하여도 높은 성능을 보여주고 있다는 것입니다.
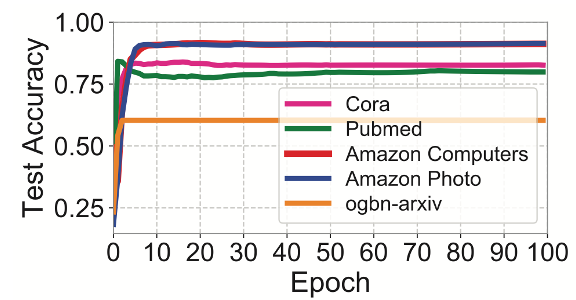
Figure 1
위의 Figure 1을 통해, MetaFP 및 제안된 approach 들이 빠르게 수렴되어, 자원이 한계적인 상황에서도 모델을 적용할 수 있다는 것을 보여주고 있습니다.
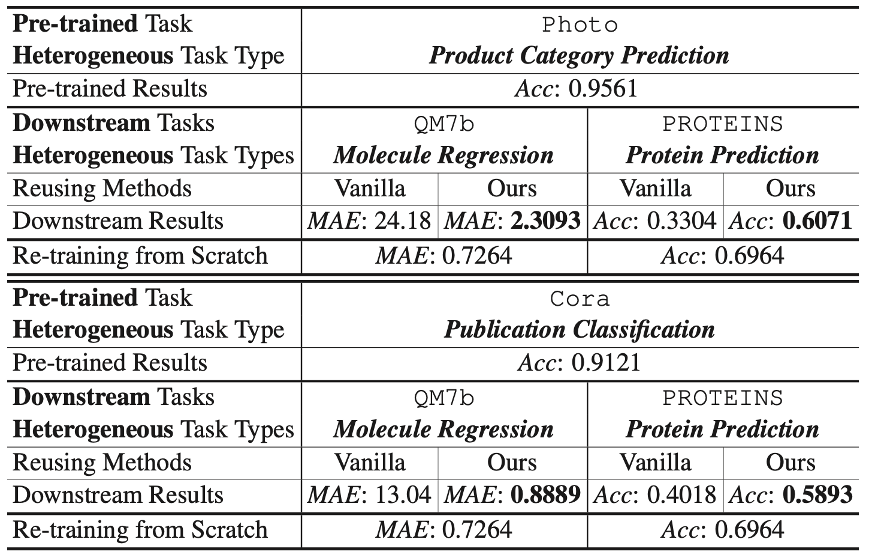
Table 4
Table 4는 node-level classification을 진행한 하나의 pre-trained model로 cross-level task(graph regression, classifcation)를 진행한 결과입니다. MetaGP를 이용하여 downstream task를 진행하였고, vanalia reusing 방법을 사용한 것보다 모두 압도적으로 우수한 성능을 이끌어낸다는 것을 볼 수 있습니다.
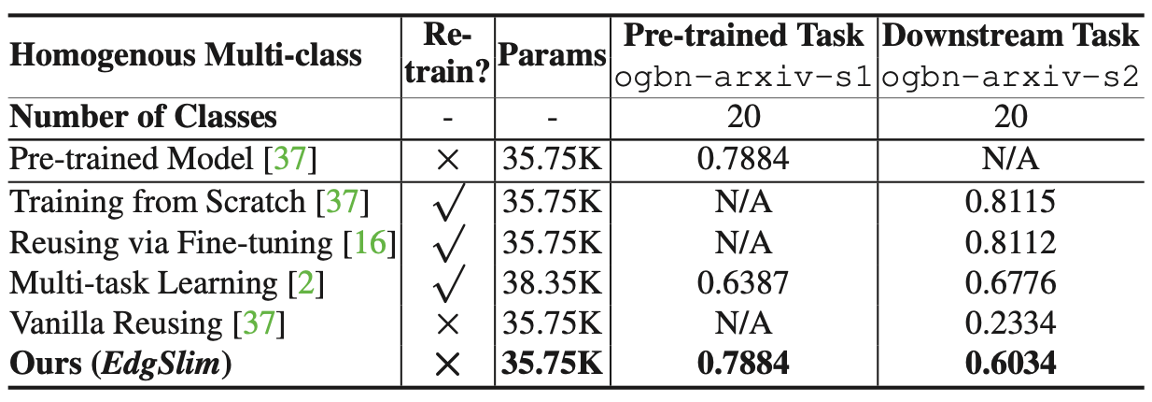
Table 5
Table 5는 homogenous domain에서 node classification을 진행하였습니다. EdgSlim은 retraining을 하지 않고도 vanila method는 물론이고, retraining을 한 모델들과 견주어도 비교할 만한 결과를 도출해 내는 것을 볼 수 있습니다.
4.2. Homogenous - Domains
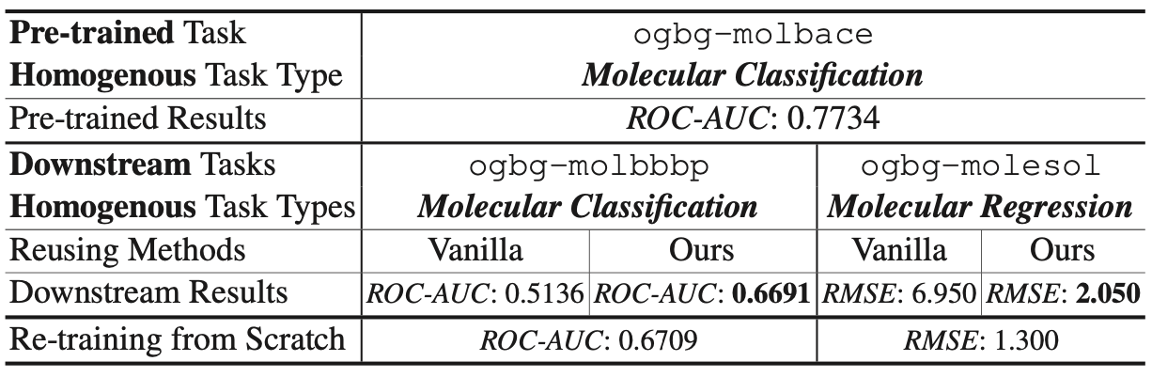
Table 6
Homogenous domain에서의 첫번째 task는 molecular property를 예측하는 것으로, MetaGP를 적용하여 하나의 pre-trained 모델로 cross-level task 진행한 것을 볼 수 있습니다. 이 실험 역시 vanilla method 보다 뛰어난 성능을 보여주고 있습니다.
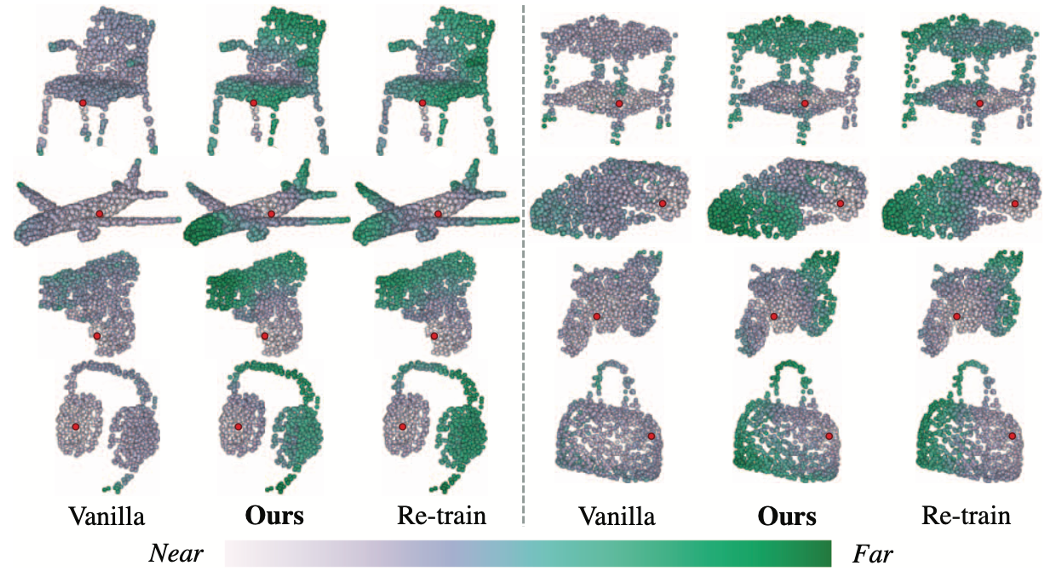
Figure 2
Figure 2는 중간 레이어 에서의 특징 공간의 구조를 보여주는데, vanilla reusing 방법과 달리 MetaGP를 적용한 reusing 방법은 처음(scratch)부터 re-training한 모델과 의미적으로 유사하다는 것을 볼 수 있습니다.

Table 7
또한 Table 7에서는 ModelNet40에 사전 훈련된 DGCNN을 ShapeNet의 다양한 downstream class에 대해 처리한 결과를 보여주는데, 이는 cross-level 뿐만 아니라 cross-domain에서의 모델 reusing이 가능하다는 것을 보여주고 있습니다.
5. Conclusions
5.1. Conclusion
본 논문에서는 하나의 pre-trained GNN을 사용하여 제한된 상황에서 다양한 cross-level 및 cross-domain에 재학습(re-training) 혹은 fine-tuning 없이 reusing 하는 패러다임을 소개하고 있습니다. 이는 크게 데이터 측면(DARE)의 Meta-FeatPadding, Edge-Slimming 그리고 Meta-GraPadding과 모델 측면(MERE)의 Reprogrammable aggregator를 통해 가능하게 하였습니다. 다양한 실험을 통해, 제한된 computation 자원 밑에서도 re-training model과 견줄만한 성능을 거둘 수 있다는 것을 보여주었습니다.
5.1. Strong Points
- Knowledge Distillation (지식 증류) 기반 모델이 아닌 새로운 paradigm을 소개하였습니다.
- 이는 retraining 혹은 fine-tuning이 필요하지 않는 장점이 있습니다.
- 제안된 방법은 자원이 극히 한정된 환경에서도 적용하기에 매우 적합합니다.
- MetaFP 및 EdgSlim은 수렴된 결과를 얻기 위해 단 한번 혹은 몇번의 epoch만을 필요로 합니다.
- MetaGP 경우, subgraph를 위해 단 10개의 노드로도 충분하다는 장점이 있습니다.
- 다양한 실험을 통해 re-training model과 견주어도 될 정도의 성능을 입증시켜 주었습니다.
5.2. Weak Points
- 모델 reprogramming 방식인 ReAgg의 효과성 입증에 대한 실험이 충분하지 않다는 점과, pre-trained model에 대한 실험은 주로 classification(분류)에 대해서만 수행되었습니다
- 제안된 방법은 GNN 사전 모델에 맞추어져 있어 다른 domain으로 일반화 하기에는 어려움이 있어 보입니다.
- Padding을 해야 할 경우 downstream task의 그래프 사이즈가 pre-trained task의 그래프 사이즈보다 작아야 된다는 단점이 존재합니다.
6. References
[1] Yang et al., “Distilling Knowledge from Graph Convolutional Networks”, CVPR 2020 (University of Sydney)
[2] Chen et al., “Model Reprogramming: Resource-Efficient Cross-Domain Machine Learning”, AAAI 2024 (IBM research)
[3] Elsayed et al., “Adversarial reprogramming of neural networks”, ICLR 2019 (Google Brain)
[4] Hambardzumyan et al., “WARP: Word-level Adversarial ReProgramming”, ACL 2021 (YerevaNN)
[5] Sun et al., “Adversarial Attack and Defense on Graph Data : A Survey”, TKDE 2022 (Lehigh University)
[6] Jang et al., “Categorical reparameterization with Gumbel-Softmax”, ICLR 2017 (Google Brain)
[7] Veit et al., “Convolutional networks with adaptive inference graphs”, IJCV 2020 (Google Research)
[8] Kaiser et al., “Discrete autoencoders for sequence models”, arxiv 2018 (Google Brain)
Author Information
Kyeongryul Lee
Affiliation: KAIST
Research Interest: Graph Neural Networks, Knowledge Graphs, Graph Machine Learning
Contact: klee0257@kaist.ac.kr
Additional Informations
- 그룹 : The University of Sydney, National University of Singapore
- Code & Github for the paper
- Not provided