[NeurIPS-2022] Contrastive Graph Structure Learning via Information Bottleneck for Recommendation
1. Problem Definition
추천시스템 분야에서 대표적인 유저 및 아이템의 표현 (representation) 방식인 협력 필터링 (Collaborative Filtering) 에 좀 더 넓은 범위의 유의미한 신호들을 반영하기 위해 유저 및 아이템의 표현에 그래프 신경망 (Graph Neural Networks) 을 적용하는 시도들이 생겨났습니다. 이는 분명히 기존 방식보다 개선된 유저 및 아이템의 표현을 만들어냈고, 추천시스템의 성능향상에 크게 기여하였습니다. 이러한 그래프 신경망에 기반한 협력필터링은 일반적으로 Graph-based Colllaborative filtering (GCF) 라고 명명합니다. GCF의 훌륭한 성능에도 불구하고, GCF의 표현 인코딩에 사용되는 데이터에 대한 큰 2가지 문제로 인해 GCF의 효과에는 제한이 발생합니다.
1. Popularity bias
모든 유저 및 아이템이 같은 interaction을 지니고 있지 않습니다. 일반적으로 추천시스템에서 사용되는 데이터는 몇몇 유저 및 아이템에 interaction이 집중된 Long-tail 분포를 지니고 있습니다. 이러한 훈련데이터의 분포는 GCF 인코더가 만들어낸 표현이 잠재공간에서 인기 유저 및 아이템 표현 인근에 집중되는 편향을 야기하게 되고, 이는 인기있는 아이템에 대한 추천은 더 빈번하게 발생하고, 그렇지 않은 아이템은 추천이 덜 발생하는 인기 편향 (popularity bias) 을 야기합니다.
2. Noisy in interactions
추천시스템에서는 유저의 명확한 성향을 알 수 있는 explicit interaction을 구하기가 굉장히 어렵습니다. 그래서 일반적으로 단순한 클릭 여부 등의 implicit한 interaction을 데이터로 활용합니다. 이러한 interaction은 랜덤 클릭, 클릭 실수 등 유저의 실제 선호와 거리가 있는 noise interaction을 포함하고 있고, 이러한 노이즈 데이터는 GCF에 굉장히 치명적인 결과를 야기합니다.
이러한 GCF의 치명적인 문제를 완화하기 위한 방법의 일환으로 대조학습 (contrastive learning) 을 GCF에 적용하는 시도들이 생겨 났습니다. 대조학습은 자기지도학습의 대표적인 방법 중 하나로 데이터 증강을 활용해 인코더가 만들어낸 표현의 노이즈에 대한 견고함을 강화하고, 인코더가 데이터의 핵심 feature를 학습하는데 도움을 줍니다.
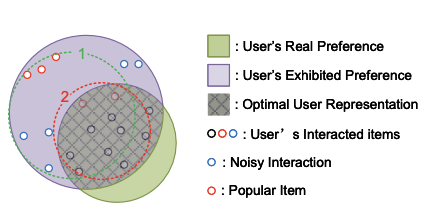
하지만 GCF에서 CL을 적용하기 위해 사용하는 데이터 증강에는 여러가지 문제가 있습니다. 이전까지는 주로 random하게 사용자 혹은 아이템의 기존 상호작용을 일부 제거하는 방식의 데이터 증강방식을 사용했습니다. 다만, 랜덤한 interaction의 제거는 위 사진처럼 GCF를 통한 표현 인코딩 과정에서 증강된 데이터의 표현이 주요한 정보들이 아닌 noise 정보들을 반영할 가능성을 야기합니다. 즉, 이러한 증강기법을 통해 만들어낸 표현은 대조학습을 통해 기존 GCF에 유의미한 효과를 만들어내지 못합니다.
또한 기존 대조학습의 프레임워크는 증강 데이터의 표현을 대조하는 방식으로 진행됐습니다. 다만 이는 위에서 언급한 잘못된 증강방식에 대한 위험 때문에 실제 추천시스템에 유효하지 않습니다.
2. Motivation
논문에선 위에서 언급한 문제들에 대한 해결방안으로 머신러닝 기반의 학습가능한 데이터 증강방식 및 새로운 GCF에서의 대조학습 프레임워크를 제시합니다.
1. 학습가능한 데이터(그래프) 방식
학습가능한 증강방식을 통해 제거할 상호작용 그래프 안에서의 상호작용 혹은 노드에 대해 선정해 제거합니다. 이 데이터 증강함수는 인기 노드에 대한 영향을 줄이고, 비인기 노드의 정보를 보호하는 방식으로 학습을 진행해 인기편향을 예방합니다.
2. 증강데이터와 기존 데이터의 결합
기존 대조학습을 적용한 시도들은 증강함수를 통해 만들어낸 그래프의 인코더 표현을 대조하는 방식으로 대조학습을 적용합니다. 이 논문에선 만들어낸 각 증강 데이터에 대한 표현을 통합시키는 아이디어를 제시합니다. 이는 각 증강데이터의 표현이 저장하고 있는 정보를 통합하는 과정으로 해석할 수 있고, 모델의 견고함을 개선하는데 도움을 줄 수 있습니다.
이때 각 증강데이터의 표현이 추천시스템에 효과적인 표현임을 보장하는 것이 정보가 통합됐을 때, 유의미한 정보로 동작할 수 있습니다. 그래서 각 표현은 추천이라는 우리의 본래 목적에 유용한 표현 이어야 합니다. 또한 이러한 제약 속에서 표현의 통합이 가장 효과적이기 위해선 각 표현이 서로 다른 유용한 정보를 담고 있어야 합니다. 이러한 표현을 얻기 위해 논문에서는 정보이론의 개념이 사용됩니다. Information Bottleneck (IB) 라는 개념을 적용하는데, 이 개념을 적용해 증강데이터와 원래 데이터 사이의 상호정보는 최소화 하면서 추천에 효과적인 증강함수를 만들어 냅니다. IB의 적용은 각 증강함수가 원래 데이터의 노이즈 상호작용을 반영하지 않게 도와줘 노이즈 상호작용에 대한 GCF 인코더의 취약성을 보완합니다.
3. Method
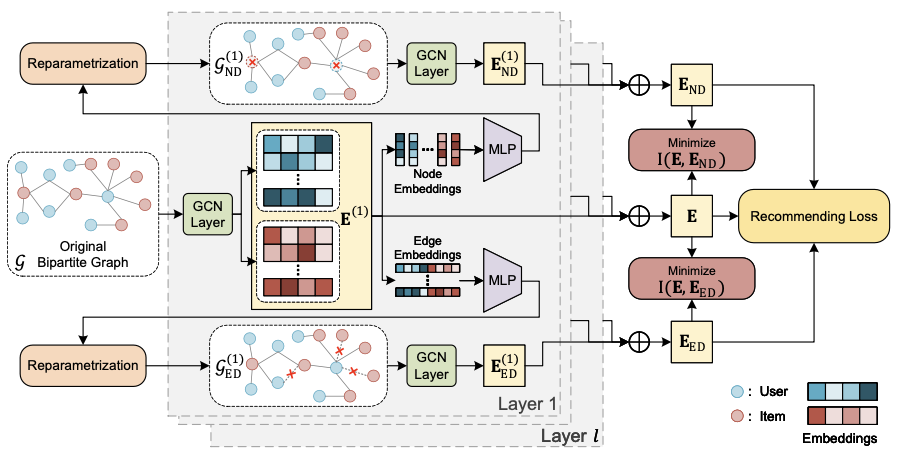
3.1 Preliminary
-
Dataset
$U \text{(user set)} = {u_{1}, u_2, u_3, …. , u_m}$
$I \text{(item set)} = {i_{1}, i_2, i_3, …. , i_n}$
$R \text{(relation matrix)} \in \mathbb{R}^{m*n}$
$(r_{u,i} = 1\text{ if there’s an interaction between user } u \text{ and itme }j \text{ else 0})$ -
GNN encoder의 동작방식 (LightGCN) 위 데이터로부터 GNN encoding을 하기 위해선 위 데이터를 Graph $G={V, E}$로 전환합니다. $V =U \cup I \text{ and } E\text{(edge)} = {e_{u,i} | r_{u,i} = 1, u \in U, i \in I}$
그리고 주어진 $R$ 로 부터 Adjacency matrix(인접행렬 A)을 만들어 사용합니다. $A =\begin{bmatrix} 0 & R \ R^T & 0 \end{bmatrix}$
추천시스템에서 GNN 인코더는 일반적인 GCN encoder의 형태로, 정해진 GCN 레이어 수만큼 이웃 노드의 표현정보를 수집하는 과정을 거쳐 최종 노드 표현을 만들어 냅니다. $\mathbf{E}^{(l)} = GCN(\mathbf{E}^{(l-1)}, G)$
이때, 추천시스템에서는 초기 노드의 표현이 모델의 학습가능한 parameter로 주어집니다. ($\mathbf{E}^{(0)}$)
행렬 수식의 관점이 아닌 노드의 표현 관점에서 수식을 재정리하면 다음과 같습니다. $e_ {u}^{(l)} = f_ {combine}(e_ {u}^{(l-1)}, f_ {aggregate}^{l}({e_ {i}^{(l-1)}|i \in N(u)})$
위 과정을 L번 거치는 동안 각 레이어의 표현을 저장해놓고, $f_ {readout}$이라는 함수를 통해 최종 표현$(e)$을 만들어 냅니다. $e = f_ {readout}({e^{l} \vert l = 0,1,2,…L})$
LightGCN의 경우 단순히 aggregation이 이웃 노드의 표현을 선형 결합하는 과정을 L번 반복해 각 레이어의 표현을 $f_{readout}$을 통과시켜 최종 표현을 얻어 냅니다. 이때 $f_{readout}$ 으로 단순히 평균이나 레이어 별 표현의 합 등이 사용되고, LightGCN의 레이어별 표현을 주어진 행렬 데이터로 다음과 같이 표현할 수 있습니다.
$\mathbf{E}^{(l)} = (D^{-0.5}AD^{-0.5}\mathbf{E}^{(l-1)})$
3.2 Main Method
이 논문에선 앞서 설명한 LightGCN 인코더를 통해 논문에서 제시하는 증강함수를 통해 생성한 각각의 증강그래프의 표현을 만들어내고 최종적으로 각 표현을 결합해 최종 표현을 만들어내게 됩니다. 그래서 이 논문의 핵심인 각각의 증강함수에 대해 설명하고자 합니다.
3.2.1 Learnable Node-Dropping
기존 단순한 랜덤하게 그래프의 노드를 제거하는 것이 아닌 이 논문에선 학습이 가능한 노드 제거 방식을 제시합니다. 이는 다음과 같이 공식화시킬 수 있습니다. $G_{ND}^{l} = ({(v_{i} \odot p_{i}^{l}|v_{i} \in V }, E)$ ($p_{i}^{l} \in {0,1}$은 학습 가능한 parameter $w_{i}^{l}$을 확률로 같는 베르누이 분포에 의해 결정됩니다.)
이렇게 레이어 별로 일부 노드가 제거된 그래프를 레이어별로 GCN 인코더에 적용해 각 레이어별 새로운 표현을 만들어내게 됩니다.
$\mathbf{E}^{(l)}_ {ND} = GCN(\mathbf{E}_ {ND}^{(l-1)}, G_ {ND}^{l})$
3.2.2 Learnable Edge-Dropping
Node Dropping과 같은 방식으로 edge 역시 일부 제거시켜 새로운 그래프를 만들어 냅니다. $G_{ED}^{l} = (V, {(e_{ij} \odot p_{ij}^{l}|e_{ij} \in E })$ ($p_{ij}^{l} \in {0,1}$은 학습 가능한 parameter $w_{ij}^{l}$을 확률로 같는 베르누이 분포에 의해 결정됩니다.)
마찬가지로, 이렇게 레이어 별로 일부 엣지가 제거된 그래프를 레이어별로 GCN 인코더에 적용해 각 레이어별 새로운 표현을 만들어내게 됩니다.
$\mathbf{E}^{(l)}_ {ED} = GCN(\mathbf{E}_ {ED}^{(l-1)}, G_ {ED}^{l})$
3.2.3 $w_{i}^{l}, w_{ij}^{l}$ 계산
각각의 노드 및 엣지를 제거할 확률인 $w_{i}^{l}, w_{ij}^{l}$다음과 같이 l번째 레이어에서 노드 및 엣지를 구성하는 노드 표현($e_{i}^{l}, e_{j}^{l}$)을 다층 신경망을 통과시켜 계산하게 됩니다.
$w_{i}^{l} = MLP(e_{i}^{l}), w_{ij}^{l} = MLP(e_{i}^{l}, e_{j}^{l})$
3.2.4 Information Bottleneck에 기반한 Training
이 논문에서는 기존 대조학습에 대해 활용하던 논문에는 없었던 새로운 목적함수를 제시합니다. 그 목적함수를 위해 사용하는 이론의 기반이 바로 정보이론에서 다루는 Information Bottleneck (IB) 입니다. IB에 기반해 이 논문의 메소드는 증강 데이터에 의한 표현과 기존 데이터의 표현 사이의 분산을 키우면서, 각각의 증강 데이터의 표현이 추천이라는 목적에 맞도록 학습방향을 조정할 수 있도록 합니다. 이를 수식으로 정리하면 다음과 같습니다.
$\min_ {E;\tilde{E}}\tilde{\mathcal{L}}_ {Rec} + I(E;\tilde{E})$ $I(E;\tilde{E})=I(E_ {u};\tilde{E_ {u}})+I(E_ {i};\tilde{E}_ {i})$
$I(;)$는 두 표현사이 상호 정보(mutual information)양. $\tilde{E}$는 $E_{ND}$, $E_{ED}$를 표현하는 표기방식(= 증강데이터를 활용해 만든 최종 노드 표현)
다음 수식을 최소화하기 위해서 상호 정보에 대한 수식이 필요합니다. 일반적으로 InfoNCE 손실함수를 최소화 하는 것이 상호 정보양에 대한 하한값을 최대화하하는 역할을 합니다. 즉, 이를 역으로 이용해 negative InfoNCE 손실함수를 최소화하는 방향으로 상호정보 양의 하한을 최대화하는 방향으로 목적함수를 설정합니다. 즉 주어진 수식에서 $I(E;\tilde{E})$를 negative InfoNCE 손실함수로 대체해 사용합니다.
$I(E_ {u};\tilde{E}_ {u}) = -{\sum_ {u \in U} \log \frac{\exp(\text{sim}(\mathrm{e}_ {i}, \tilde{\mathrm{e}_ {i}}) / \tau)}{\sum_ {j\in U} \exp(\text{sim}(\mathrm{e}_ {i}, \tilde{\mathrm{e}}_ {j}) / \tau)}}$ (sim = Cosine similarity, $\tau$= temperature(하이퍼파라미터))
위 수식은 추천시스템의 목적함수와 함께 multi-task 최적화에 활용됩니다. $\mathcal{L} = \mathcal{L}_ {rec} +\mathcal{L}_ {rec}^{ND}++\mathcal{L}_ {rec}^{ED} + \lambda(I(E;\tilde{E}_ {ND})+I(E;\tilde{E}_ {ED})) + \beta||\theta||^{2}_ {2}$
4. Experiment
- 실험데이터: Yelp2018, MovieLens-1M, Douban (Training:Validation:Test = 8:1:1)
- 평가지표: Recall@10, 20 / NDCG@10, 20
- 비교 Baseline 모델: PRMF, NCF, NGCF, LightGCN, DNN+SSL, SGL
4.1 실험결과(Baseline과 추천 성능 비교)
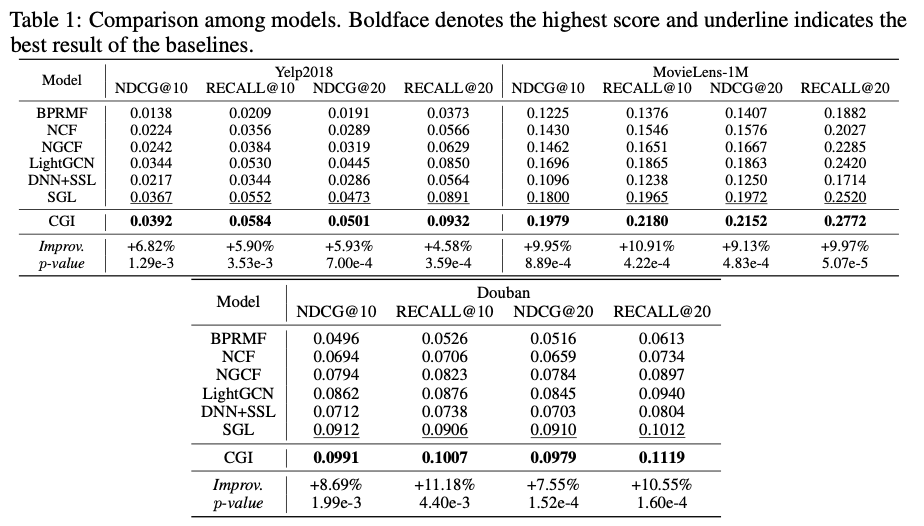 CGI(논문 메소드)가 세가지 실험 데이터셋 모두에서 모든 베이스라인의 성능지표를 압도함.
(두번째로 높은 성능을 보인 SGL보다 Yelp 데이터에서 약 5.9%, MovieLens-1M 데이터 약 10% , Douban 데이터 약 10% 성능 개선)
CGI(논문 메소드)가 세가지 실험 데이터셋 모두에서 모든 베이스라인의 성능지표를 압도함.
(두번째로 높은 성능을 보인 SGL보다 Yelp 데이터에서 약 5.9%, MovieLens-1M 데이터 약 10% , Douban 데이터 약 10% 성능 개선)
4.2 실험결과(보충실험)
-
Random Dropout 증강방식과의 비교
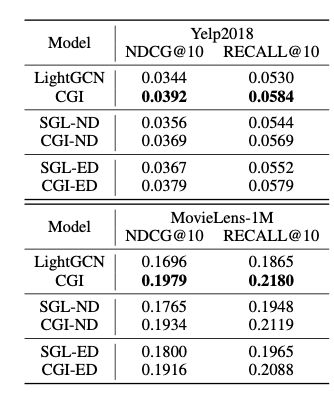 Node dropout, Edge dropout 모두 이 논문이 제시한 것처럼 학습가능한 함수를 통해 dropout을 하는 것이 단순히 랜던함 dropout방식보다 성능이 개선됨.
Node dropout, Edge dropout 모두 이 논문이 제시한 것처럼 학습가능한 함수를 통해 dropout을 하는 것이 단순히 랜던함 dropout방식보다 성능이 개선됨. -
GCF 문제 개선
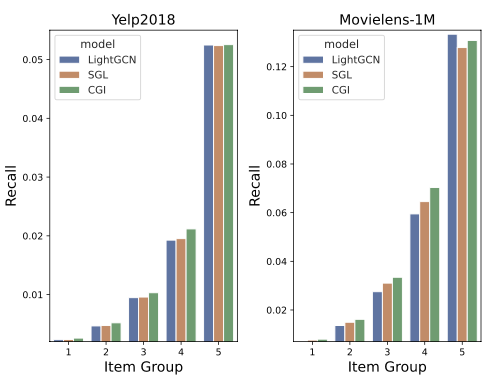 실제 interaction이 적은 item의 추천 비중을 단순한 GCF 모델과 SGL 모델보다 개선함을 확인함. (Poularity bias 완화)
실제 interaction이 적은 item의 추천 비중을 단순한 GCF 모델과 SGL 모델보다 개선함을 확인함. (Poularity bias 완화)
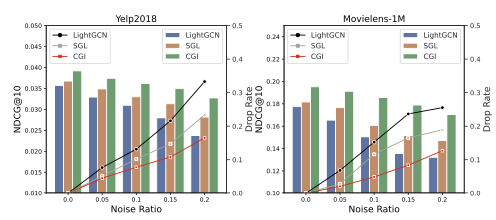 노이즈를 일부로 추가한 데이터에서도 다른 비교 모델이 비해 성능 떨어짐 감소. (Noise robustness 증가)
노이즈를 일부로 추가한 데이터에서도 다른 비교 모델이 비해 성능 떨어짐 감소. (Noise robustness 증가) -
Information Bottleneck의 효과 Information Bottleneck를 고려하지 않은 다른 모델들과 비교시 Information Bottleneck을 고려한 논문의 모델이 최적화 당시 더 나은 local minimum으로 향해 가는 것을 확인할 수 있음.
Result(Discussion)
이 논문은 learnable한 그래프 증강방식을 소개함으로써, 그래프에서 대조학습을 위한 증강과정에서 core-interaction을 없애는 걸 막을 수 있었다.
다만, 이는 모델의 파라미터 복잡도를 높일수 밖에 없고, 추천시스템의 implicit interaction에서 noise를 명확하게 정의할 수 없다는 한계로 인해 드롭아웃 ratio($w_{i}, w_{ij}$)가 충분히 학습된다고 해도, 핵심 상호작용 제거에 대한 위험이 존재한다.(주어진 데이터로 학습한다는 것도 문제가 될 수 있다고 생각한다.)
하지만 이 논문의 메소드를 통해 그 위험의 정도를 낮추고, Multi-view representation과 Information Bottleneck이라는 아이디어는 앞으로도 GCF 도메인에서 Augmentation을 사용하는 인코딩에 자주 활용될 수 있을 거란 점에서 좋은 인사이트를 준 논문이었다고 생각한다.
Source Code(Materials)
https://github.com/weicy15/CGI