[ICML-24] Class-Imbalanced Graph Learning without Class Rebalancing
1. Problem Definition
그래프 데이터에는 각 노드에 라벨링이 되어 있지 않은 경우가 많으며, 그 중에서도 각 분류군마다 노드의 수와 각 분류군마다 라벨링이 된 노드의 수가 크게 차이나는 경우가 많다. 최근 연구에 따르면, 그래프의 노드 중에서 그래프 신경망 모델(Graph Neural Networks, GNNs)은 라벨링이 적거나 개수가 적은 분류군의 노드에 대해서 노드 분류 (Node Classification) 성능이 떨어지는 경우가 많다. 논문에서는 이러한 분류군 불균형 문제 해결을 위해서 Class-Imbalanced Graph Learning(CIGL) 기법을 제안한다.
일반적으로 imbalance-handling 기법들은 분류군 사이 균형을 맞추는 방식으로 접근을 해오고 있으며, 이러한 메커니즘을 Class Rebalancing (CR) 이라고 한다. CR 기법은 크게 reweighting과 resampling 기법으로 나눌 수가 있다. 최근에는 기존 CR 메커니즘 외에 그래프의 라벨링된 노드들의 위상적 불균형(topological imbalance)을 다루는 연구가 등장했다. 이러한 연구에서 착안하여 논문 에서는 기존 CR 메커니즘의 틀에서 벗어나서 그래프 형태의 데이터가 갖는 위상적 특성(topological property)을 활용한 CIGL 방법을 제시한다.
그래프의 위상적 불균형 측면에서 CIGL 접근을 하는 이유는 크게 두 가지로 볼 수가 있다. 첫번째는 그래프 데이터의 다른 데이터와는 다른 특징 중 하나인 구조적인 정보를 고려할 수 있다는 점이다. 두번째로 기존 CR 기법과 같이 사용이 가능하다는 점이다.
2. Relationship between Class Imbalance and Local Topology
논문에서는 Ambivalent Message-Passing (AMP)와 Distant Message-Passing (DMP) 두 가지를 정의하여 그래프의 local topology를 분석한다. 두 가지 내용에 앞서서 논문에서는 다음과 같은 배경을 설정한다.
-
그래프가 Stochastic Block Model을 따른다. [5]
-
SBM($\mathcal{n}$, $\mathcal{p}$, $\mathcal{q}$): 전체 $\mathcal{n}$개의 노드는 $\mathcal{p}$의 확률로 같은 클래스의 노드와 연결되고, $\mathcal{q}$의 확률로 다른 클래스의 노드와 연결된다.
-
이렇게 얻은 그래프를 노드의 집합 $\mathcal{V}$와 엣지의 집합 $\mathcal{E}$로 $\mathcal{G}$: ($\mathcal{V}$, $\mathcal{E}$)와 같이 정의한다.
-
-
$\mathcal{H}$($\mathcal{u}$, $\mathcal{k}$): 타겟 노드 $\mathcal{u}$의 $\mathcal{k}$-hop homo-connected 이웃들의 집합
- 만약 노드 $\mathcal{u}$에서 노드 $\mathcal{v}$로의 path [$\mathcal{u}$, $\mathcal{v_ {1}}$, … ,$\mathcal{v_ {k}}$, $\mathcal{v}$]에서 $\mathcal{v_ {1}}$, … ,$\mathcal{v_ {k}}$, $\mathcal{v}$가 모두 같은 class 이면, 노드 $\mathcal{u}$가 노드 $\mathcal{v}$와 homo-connected라고 한다.
-
이진 분류를 수행한다고 가정하고, 전체 $\mathcal{n}$개의 노드 중에서 $\mathcal{n_ {1}}$개의 노드가 minority class에 해당하고, $\mathcal{n_ {2}}$개의 노드가 majority class에 해당한다.
- $\mathcal{n}$ = $\mathcal{n_ {1}}$ + $\mathcal{n_ {2}}$이고, $\mathcal{n_ {1}}$ $\ll$ $\mathcal{n_ {2}}$
-
$\mathcal{V_ {i}}$: class $i$의 노드 집합
-
$\mathcal{V}_ {i} ^ {L}$: class $i$의 노드 중 라벨링이 된 노드의 집합
-
불균형 비율 (imbalance ratio, $\rho$) $\colon= \frac{n_ {2}}{n_ {1}}$
이와 더불어서 관습적으로 받아들여지는 가정을 사용한다. [6]
-
$n_ {1} \cdot p = \beta + O(\frac{1}{n})$
- $\beta$는 minority class 노드들의 intra-class node degree를 의미한다.
-
$\frac{p}{q} = O(1)$
2. 1. Ambivalent Message-Passing (AMP)
노드 $\mathcal{u}$에 대한 $\mathcal{k}$-hop AMP 계수는 다음과 같이 정의된다.
$\alpha^ {k}(u) \colon= \frac{\vert {v\vert v \notin \mathcal{V}_ {i}, v \in \mathcal{H}(\mathcal{u}, \mathcal{k})} \vert}{\vert {v\vert v \in \mathcal{V}_ {i}, v \in \mathcal{H}(\mathcal{u}, \mathcal{k})} \vert}$
논문에서 정의한 AMP는 노드의 이웃 노드에 heterophilic한 노드의 비중을 나타내기 위한 지표라고 볼 수 있다. Heterophily란, 두 노드가 서로 다른 class에 속하는데 이웃하는 경우를 의미한다. 이는 하나의 그래프에 다수의 노드 class와 엣지 class가 존재한다는 heterogeneous와는 의미가 다르다. AMP 계수를 class 별로 구할 수도 있는데, class $i$에 대한 $k$-hop AMP 계수는 다음과 같다.
$\alpha^ {k} _ {i} \colon= \frac{\mathbb{E}_ {u \in \mathcal{V}_ {i}}[\vert {v\vert v \notin \mathcal{V}_ {i}, v \in \mathcal{H}(\mathcal{u}, \mathcal{k})} \vert]}{\mathbb{E}_ {u \in \mathcal{V}_ {i}}[\vert {v\vert v \in \mathcal{V}_ {i}, v \in \mathcal{H}(\mathcal{u}, \mathcal{k})} \vert]}$
이를 기반으로 다음과 같이 정리할 수가 있으며, 자세한 증명은 논문을 참고하는 것을 추천한다.
Theorem 2. 1 (AMP로 인한 편향성).
전체 노드 수 $n$이 충분히 클 때, majority class의 AMP 계수에 대한 minority class의 AMP 계수의 비는 불균형 비율($\rho$)에 polynomially 비례하며, $k$-hop에 exponentially 비례한다.
$\frac{\alpha_ {1} ^ {k}}{\alpha_ {2} ^ {k}} = \left( \rho \cdot \frac{\sum_ {t=1} ^ {k} (\rho \beta)^ {t-1}}{\sum_ {t=1} ^ {k} \beta^ {t-1}} \right)^ {2} + O\left( \frac{1}{n} \right)$
따라서, 불균형 비율이 클수록 AMP에 대한 minority class 노드들의 상대적인 취약도가 더 커진다고 볼 수 있다.
2. 2. Distant Message-Passing (DMP)
노드 $\mathcal{u}$에 대한 $\mathcal{k}$-hop DMP 계수는 다음과 같이 정의된다.
$\delta^ {k}(u) \colon= \mathbb{1}{(L_ {i} ^ {k}(u)=0, \sum_ {j} L_ {j} ^ {k}(u) > 0)}$, where $L_ {j} ^ {k}(u) = \vert {v \vert v \in \mathcal{V}_ {j} ^ {L}, v \in \mathcal{H}(\mathcal{u}, \mathcal{k}) } \vert$
논문에서 정의한 DMP는 타겟 노드의 class와 동일한 class의 노드이면서 라벨링이 된 노드가 얼마나 떨어져 있는지를 파악하기 위한 용도이다. DMP 계수 역시 class 별로 구할 수 있으며, class $i$에 대한 $k$-hop DMP 계수는 다음과 같다.
$\delta^ {k} _ {i} \colon= \mathbb{P}(\delta^ {k}(u) = 1)$, where $u \in \mathcal{V}_ {i}$
Theorem 2. 2 (DMP로 인한 편향성).
class $i$의 라벨링된 데이터의 비율을 $r_ {i} ^ {L} \colon= \frac{\vert \mathcal{V}_ {i} ^{L} \vert}{\vert \mathcal{V}_ {i} \vert}$이고, 전체 노드 수 $n$이 충분히 클 때, majority class의 DMP 계수에 대한 minority class의 DMP 계수의 비는 불균형 비율($\rho$)에 exponentially 비례한다.
$\frac{\delta_ {1} ^ {k}}{\delta_ {2} ^ {k}} \approx \frac{1-r_ {1} ^ {L}}{1-r_{2} ^ {L}}e^ {(\rho-1)\beta} + O\left( \frac{1}{n} \right)$
따라서, DMP에 대한 minority class 노드들의 상대적인 취약도 역시 불균형 비율($\rho$)이 커질수록 더 커진다고 볼 수 있다. 여기서 중요한 것 중 하나는 단순히 minority class 노드를 더 라벨링을 한다고 해서 편향성이 크게 바뀌지 않는다는 것이다. 물론, 이것이 편향성을 완화할 수는 있겠지만, 불균형 비율($\rho$)가 상대적으로 더 큰 영향을 끼칠 수 있다는 것을 보여준다.
2. 3. 실험적 분석
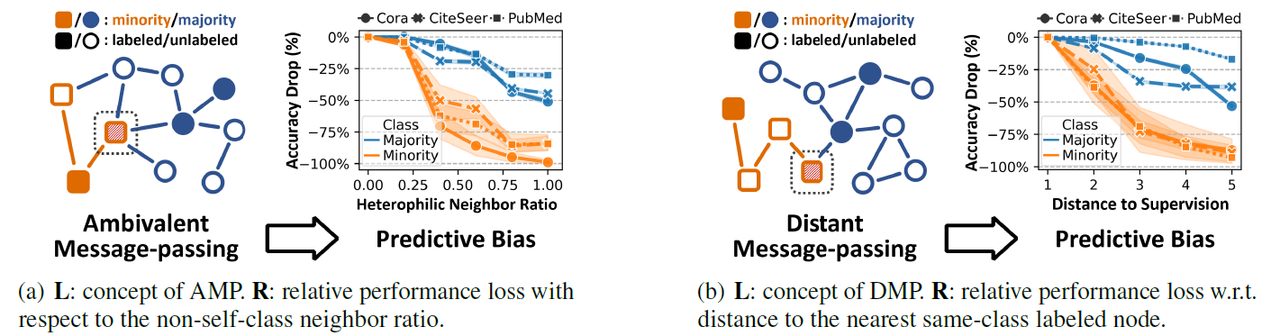
위 그림은 그래프에 포함된 각 노드의 AMP와 DMP 계수가 실제로 노드 분류 모델의 성능 저하와 상관성이 있다는 것을 보여준다. 왼쪽 그림을 보면 실제로 AMP 계수의 정도가 큰(heterophily 특성이 높은) 경우에 모델의 성능 저하가 더 큰 경향이 있다는 것을 보여준다. 특히, AMP 계수에 대해서 minority class가 majority class 보다 영향을 더 많이 받는 다는 것을 관찰할 수 있으며, 이는 Theorem 2. 1과 맞는 결과라고 볼 수 있다.
오른쪽 그림을 보면, 각 노드나 class의 k-hop DMP 계수는 0과 1 값으로 표현되고, 이때 1이 되는 최소 k가 “distance to supervision”이라고 볼 수 있다. 이를 해석해보면, 같은 class이면서 라벨링된 노드가 더 가까이 있을수록 모델의 성능 저하가 작다고 볼 수 있다. 특히, minority class가 majority class 보다 상대적으로 더 영향을 많이 받는 다는 것을 관찰할 수 있으며, 이는 Theorem 2. 2와 맞는 결과라고 볼 수 있다.
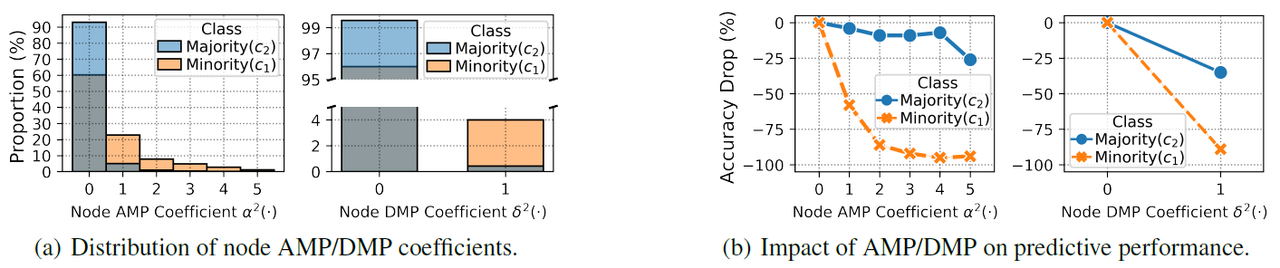
위 그림은 PubMed 데이터셋과 Graph Convolutional Network(GCN) 모델을 사용해서 측정한 결과로 2-hop을 기준으로 AMP와 DMP 계수를 계산한 결과이다. 왼쪽을 보면, minority class가 majority class보다 상대적으로 AMP와 DMP 계수가 큰 노드의 비율이 크다는 것을 확인할 수 있다. 오른쪽을 보았을 때, 실제로 AMP와 DMP 계수가 더 높을수록 모델의 분류 성능 저하가 커지는 성향이 minority class에서 더 잘 나타나는 것을 관찰할 수 있었다.
이러한 분석을 근거로 논문에서는 AMP와 DMP에 영향을 많이 받는 노드를 찾고, 이러한 노드를 가상 노드(virtual node)와 연결하는 방식으로 위상적 불균형을 완화하고자 하였다.
3. Method - BAlanced Topological augmentation (BAT)
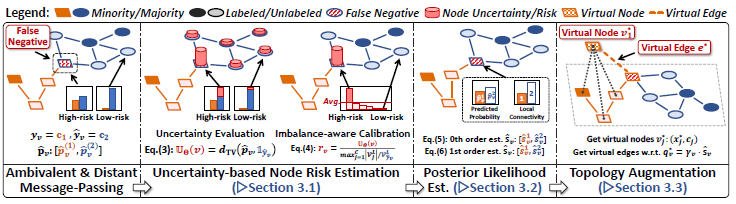
논문에서 제시한 그래프 증강 기법인 BAlanced Topological augmentation (BAT)의 목표는 잠재적으로 모델이 잘못 분류했을 가능성이 높은 노드를 가상 노드(virtual node)와 연결하여 비슷한 패턴의 노드들을 연결하는 것으로 볼 수 있다. 즉, 비슷한 패턴을 보이는 노드를 연결하여 AMP로 인한 편향을 완화할 수 있으며, 서로 인접하지 않은 노드들이 멀리 떨어진 노드와 연결될 수 있다는 측면에서 DMP로 인한 편향 역시 완화할 수 있다.
3. 1. Node Misclassification Risk Estimation
가장 먼저 수행해야하는 것은 AMP와 DMP에 취약한 노드가 무엇인지를 찾아내는 것이다. 그런데 여기서 모든 노드의 AMP와 DMP 계수를 다 계산하는 것은 cost가 커서 실제로 적용이 힘들다. 그래서 저자들은 모델의 예측 불확실성(model prediction uncertainty)을 AMP와 DMP로 인해 노드가 잘못 분류될 위험(risk)를 추정하는 방향으로 접근한다.
Uncertainty quantification
$C$를 클래스의 개수, $F(\cdot; \Theta)$는 그래프를 증강하는 시점에서의 모델, $\mathbf{A}$는 그래프의 인접 행렬, $\mathbf{X}$는 노드의 feature 행렬, $\hat{\mathbf{\mathit{p}}}_ {v}=F(\mathbf{A}, \mathbf{X}; \Theta)$ 는 모델의 예측 결과, $\hat{y}_ {v}$를 예측된 레이블이라고 할때, 불확실성 점수(uncertainty score)는 다음과 같이 정의한다.
$\mathbb{U}_ {\Theta}(v) \colon= d_ {TV}(\hat{\mathbf{\mathit{p}}}_ {v}, \mathbb{1}_ {\hat{y}_ {v}})=\frac{1}{2} \sum_ {j=1} ^ {C} \vert \hat{\mathbf{\mathit{p}}}_ {v} ^ {(j)} - \mathbb{1}_ {\hat{y}_ {v}} ^ {(j)} \vert \in [0, 1]$
논문에서는 거리 측정을 위해서 total variance 거리를 사용했는데, 거리 측정에 특정한 메트릭을 사용해야 한다는 제한은 없다.
Imbalance-calibrated misclassification risk
위의 과정으로 구하는 불확실성 점수(uncertainty score)를 바로 사용하게 된다면 대부분의 minority-class 노드를 리스크가 높다고 판단할 수가 있다는 문제가 있다. 따라서 각 class 마다 라벨링이 된 노드의 상대적인 수에 따라서 불확실성 점수(uncertainty score)를 불균형 정도에 따라 스케일링을 해줄 필요가 있다. 노드 $v$에 대한 리스크는 아래와 같이 정의한다.
$r_ {v} \colon= \frac{\mathbb{U}_ {\Theta}(v)}{\max_ {j=1} ^ {C} \vert \mathcal{V}_ {j} ^ {L} \vert / \vert \mathcal{V}_ {\hat{y}_ {v}} ^ {L} \vert} \in [0, 1]$
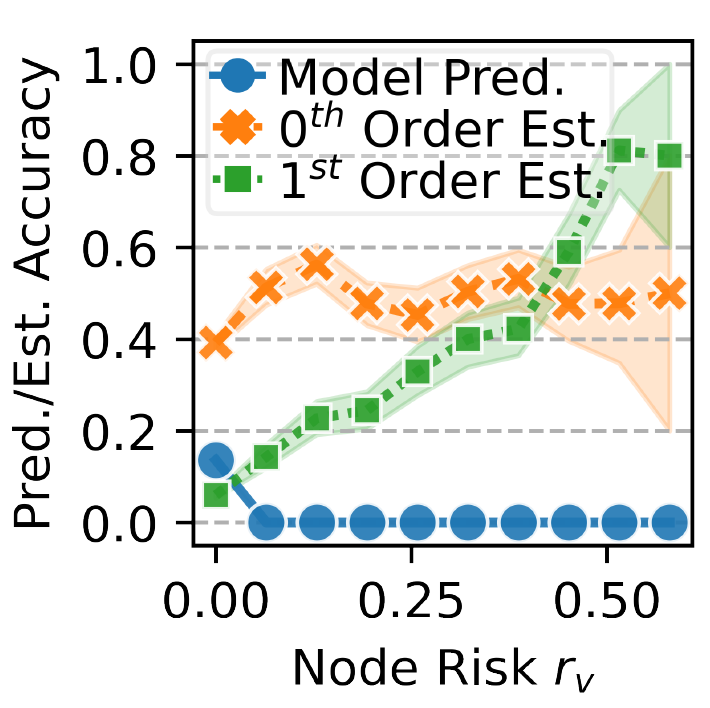
위의 리스크 측정을 사용하여 minority-class가 라벨링된 노드가 적을수록 리스크 값이 더 작아지도록 한다고 이해할 수 있다. 아래 사진은 노드의 리스크 값에 따른 예측 성능의 변화를 보여주며, 일반적으로 리스크가 높을수록 예측 정확도가 떨어진다고 확인할 수 있다.
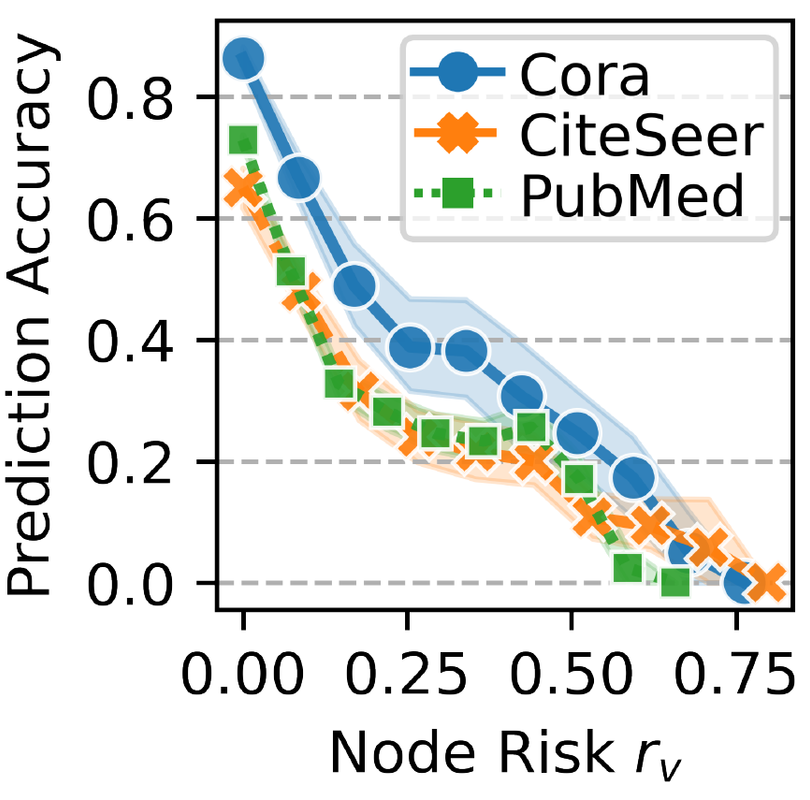
3. 2. Posterior Likelihood Estimation
앞에서 말한 방법을 통해 리스크가 높은 노드를 찾았으니, 이제 노드에 가상 노드(virtual node)를 연결하는 기준을 설정해야 한다. 그 기준으로 논문에서는 posterior likelihood를 사용한다. 기본적으로 리스크가 높은 노드는 현재 예측 결과가 틀렸을 확률이 높다는 가정에서 시작한며, 두 가지 방법을 제안하고 있다.
Zeroth-order estimation
오직 모델이 예측한 확률 결과만을 사용하며, 그래프의 구조는 사용하지 않는 방법으로 class $j$에 노드 $v$가 속할 posterior likelihood $\hat{s}_ {v} ^ {(j)}$는 다음과 같이 정의된다.
$\hat{s}_ {v} ^ {(j)} \colon= \mathbb{P}_ {y \sim\hat{\mathbf{\mathit{p}}}_ {v}}[y=j \vert y \neq \hat{y}_ {v}]=\begin{cases} \hat{p}_ {v} ^ {(j)} / (1-\hat{p}_ {v} ^ {(\hat{y}_ {v})}) & \text{, if } j \neq \hat{y}_ {v} \ 0 & \text{, otherwise.} \end{cases}$
위의 연산을 수행하기 위해서는 각 노드마다 각 class에 해당하는 posterior likelihood를 구하기 위해서 $O(\vert \mathcal{V}\vert C )$의 복잡도를 가진다.
First-order estimation
노드 $v$의 이웃 노드의 집합인 $\mathcal{N}(v)$에 대한 예측 결과를 활용하는 방법으로, $v$의 임의의 이웃 노드($v’ \sim \mathcal{N}(v)$)가 homophily 특성이 강한 그래프에서 일반적으로 $v$와 같은 class일 가능성이 크다는 점을 활용하기 위한 방법으로 볼 수 있다. Class $j$에 노드 $v$가 속할 posterior likelihood $\hat{s}_ {v} ^ {(j)}$는 다음과 같이 정의된다.
$\hat{s}_ {v} ^ {(j)} \colon= \mathbb{P}_ {v’ \sim \mathcal{N}_ {v}}[\hat{y}_ {v’}=j \vert \hat{y}_ {v’} \neq \hat{y}_ {v}]=\begin{cases} \frac{\vert { v’ \in \mathcal{N}(v) \vert \hat{y}_ {v’}=j } \vert}{\vert \mathcal{N}(v) \vert - \vert { v’ \in \mathcal{N}(v) \vert \hat{y}_ {v’}=\hat{y}_ {v} } \vert} & \text{, if } j \neq \hat{y}_ {v} \ 0 & \text{, otherwise.} \end{cases}$
위의 연산을 수행하기 위해서는 거의 모든 엣지마다 각 class에 해당하는 posterior likelihood를 구하기 위해서 $O(\vert \mathcal{E}\vert C )$의 복잡도를 가진다.
특이사항 중 하나는 논문에서는 Zeroth-order estimation과 First-order estimation 이외에 더 높은 order를 고려하지는 않는다. 그러한 이유는 complexity가 너무 높아지기 때문이라고 밝혔다. 실제로 구한 posterior likelihood를 이용해서 리스크가 높은 노드를 분류한 경우에 모델보다 더 좋은 성능을 보이는 것을 아래 그림을 통해 확인할 수가 있었다. 아래 그림은 PubMed 데이터셋에서 GCN 모델을 사용하였다.
3. 3. Virtual Topology Augmentation
BAT에서는 각 class 마다 대응되는 가상 노드를 만든다. 모델이 j class로 예측한 모델의 집합을 $\hat{\mathcal{V}}_ {j}$이라고 할 때, 다음과 같이 각 class j의 가상 노드($v_ {j} ^ {*}$)의 feature와 레이블을 설정한다.
$\mathcal{x}_ {v_ {j} ^ {*}} \colon= \sum_ {v \in \hat{\mathcal{V}}_ {j}} \mathcal{x}_ {v} / \vert \hat{\mathcal{V}}_ {j} \vert$
$y_ {v_ {j} ^ {*}} \colon= j$
생성한 가상 노드에 리스크가 높은 노드를 연결해줘야 하는데, 이 과정에서 앞서서 정의한 posterior likelihood에 비례하는 확률로 연결될 확률을 설정한다. 그러나 posterior likelihood를 바로 사용할 경우 불필요한 가상 엣지(virtual edge)가 리스크가 낮은 노드와 가상 노드 사이에 생길 수가 있다는 문제가 있다. 따라서 다음의 조건을 만족하는 할인율 $\gamma_ {v}$을 posterior likelihood $\hat{s}_ {v} ^ {(j)}$에 곱하여 사용하게 된다.
$min_ {\gamma \geq 0} \left( -\sum_ {v \in \mathcal{V}} (r_ {v} - \bar{r}_ {\hat{y}_ {v}})\gamma_ {v} + \frac{1}{2}\vert\vert \gamma \vert\vert_ {2} ^ {2} \right)$, where $\bar{r}_ {j} \colon= \sum_ {v \in \hat{\mathcal{V}}_ {j}} \frac{r_ {v}}{\vert \hat{\mathcal{V}}_ {j} \vert}$
최종적으로 사용하는 $j$ class에 대응되는 가상 노드와 리스크가 높은 노드($v$)를 연결하는 가상 엣지를 생성하는 확률은 다음으로 정의된다.
$q_ {v} ^ {(j)} \colon= \gamma_ {v}\hat{s}_ {v} ^ {(j)}$
4. Experiments
Experiment setup
-
Dataset
-
인용 네트워크(Citation networks): Cora, CiteSeer, PubMed
-
공동 저자 네트워크(Co-author networks): CS, Physics
-
-
Backbone Models
-
Graph Convolutional Network (GCN)
-
Graph Attention Network (GAT)
-
GraphSAGE
-
-
Baseline
-
일반적인 CR 기법: Reweight, Resample, SMOTE
-
그래프 데이터 특화 CR 기법: ReNode, GraphSMOTE, GraphENS
-
-
Evaluation Metric
-
Accuracy, Macro-F1: 기본적으로 논문에서 다루는 task는 노드 분류이고, 일반적으로 사용하는 분류 metric을 사용한다.
-
PerfStd: 모든 class 사이에 accuracy의 표준편차를 구한 것으로 PefrStd가 낮을수록 서로 다른 class 사이에 성능 불균형이 적다는 것으로 이해할 수 있다.
-
Result
Main Result
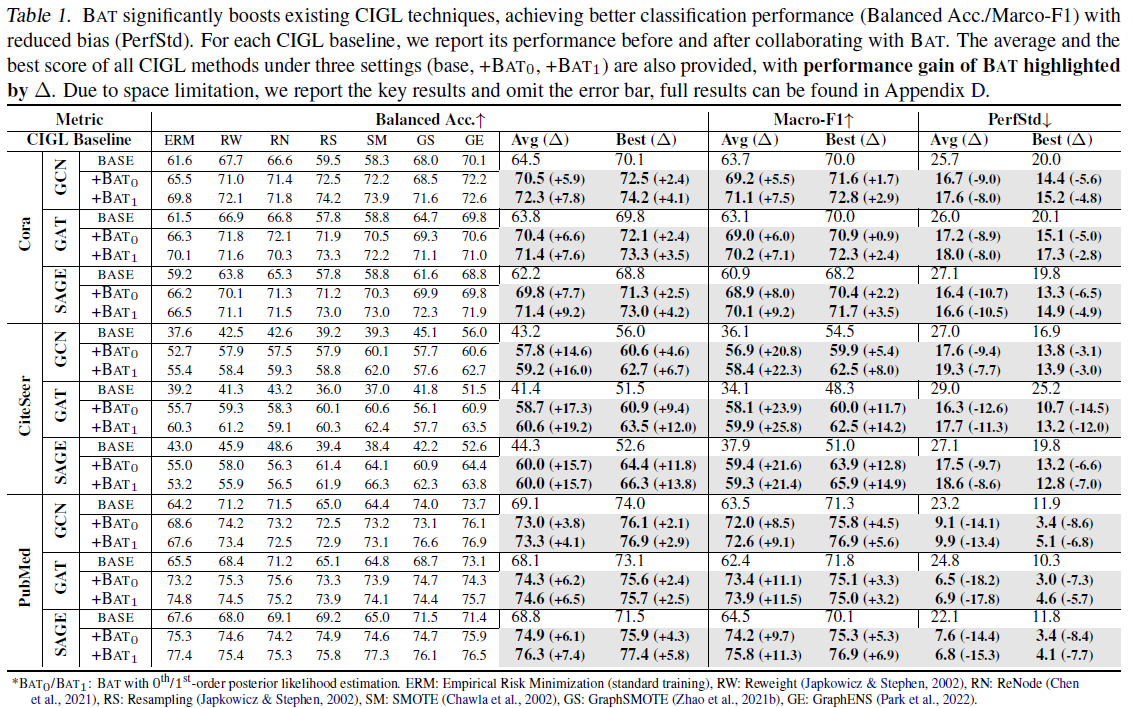
아래 표는 backbone 모델로 GCN, GAT, GraphSAGE(SAGE)를 사용하여 3개의 데이터셋 Cora, Citeseer, PubMed의 node classification 성능을 보여주는 표이다. CIGL baseline 방법 중에서 ERM은 Empirical Risk Minimization으로 특별한 CIGL 기법을 적용하지 않고 학습을 진행한 것을 의미한다. $BAT_ {0}$와 $BAT_ {1}$은 논문에서 제시한 기법을 추가로 적용한 것을 의미하는데, 각각 zeroth-order estimation과 first-order estimation을 이용하여 posterior likelihood estimation을 진행한 것이다. 실험 결과를 보면 알 수 있듯이, 일부 성능 중에서 그래프 데이터의 특성을 고려했던 기존 CIGL 기법인 GraphENS(GE), GraphSMOTE(GS), RN(ReNode)와 비교했을 때 BAT만을 적용하면 성능이 잘 나타나지 않는 것을 볼 수 있다. 그러나 BAT의 경우 다른 CIGL 기법과 같이 사용이 되었을 때, 성능 상승을 달성했다는 부분에서 기존 기법들이 다루지 못하는 측면에서 CIGL 효과를 줄 수 있다는 부분에서 의미가 있다고 볼 수 있다. 더불어 BAT의 경우 다른 기법과 비교했을 때, Macro-F1과 PerStd 성능을 통해 불균형한 분포에도 서로 다른 클래스 사이에서도 성능 격차가 적다는 부분도 유의미한 결과로 볼 수 있다.
Robustness
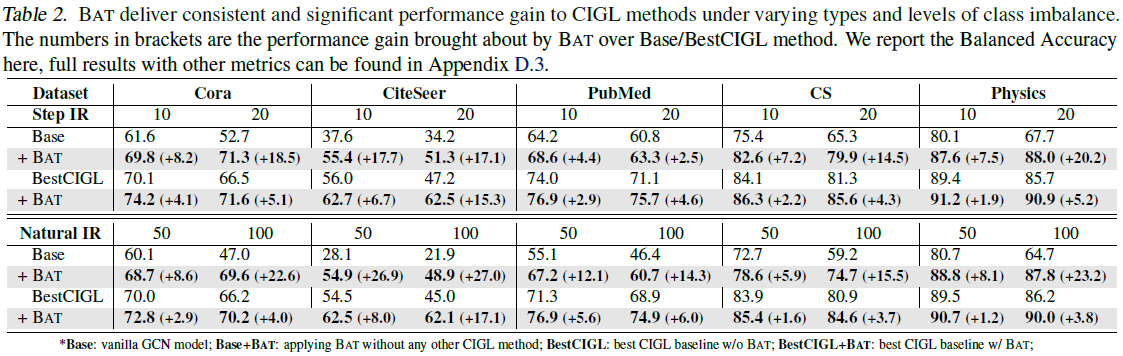
아래 표는 다섯 가지의 데이터셋에 대해서 불균형 비율($\rho$)에 따른 성능 저하 정도를 보여주는 실험 결과이다. Base는 CIGL 기법이 적용되지 않은 경우를 의미하고, BestCIGL은 baseline 중에서 가장 성능이 좋았던 기법을 의미한다. 전체적인 변동폭을 보면, BAT 가 불균형 비율이 높은 상황에서도 성능 저하 폭을 줄인다는 것은 확인할 수 있었다. 그러나 BestCIGL과 BAT만을 사용한 경우를 비교했을 때, BAT가 다른 baseline 모델에 비해서 robustness가 높다고 판단하기에는 무리가 있어 보인다. 특히, CS와 PubMed 데이터셋에 대해서는 BestCIGL과 Base에 BAT를 적용한 두 경우를 비교했을 때, BestCIGL의 성능이 더 좋다는 점을 확인할 수 있다. 이러한 점을 고려했을 때, BAT 기법이 모델의 불균형 비율에 대한 robustness를 향상할 수 있는 것은 맞지만, 그 정도가 다른 기법에 비해서 더 좋다고 하기에는 어려움이 있다고 정리할 수 있다. 이 실험 간에 특이사항 중 하나는 각 데이터셋의 불균형 비율을 조절하기 위해서 minority 클래스의 노드 일부를 무작위로 삭제하는 방식으로 진행이 되었다. 이 부분에서 기존 데이터셋의 구조적인 정보가 훼손될 수 있다는 점에서 실험이 합리적으로 이루어진 것이 맞는지에 대해서도 논란의 여지가 있다고 생각한다.
AMP & DMP
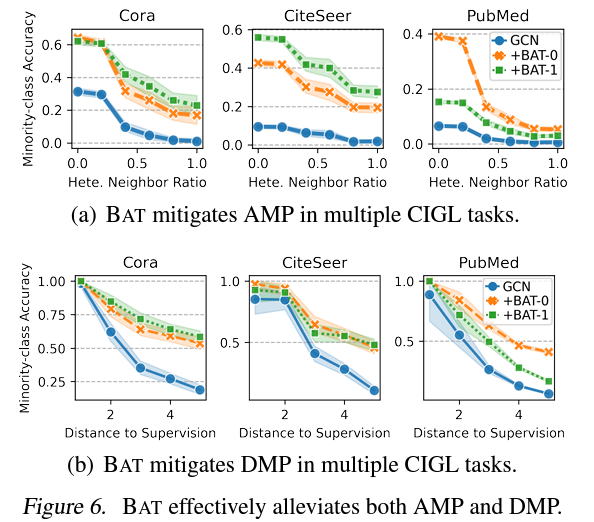
아래 그림은 실제로 BAT 기법을 적용했을 때, AMP와 DMP의 변화량에 관한 실험 결과를 보여준다. 실제로 BAT 모델을 적용한 경우 AMP를 나타내는 Heterophilic Neighbor Ratio가 높은 노드에서도 minority-class에 대한 정확도 감소량이 적은 것을 확인할 수 있다. 또한 DMP를 보여주는 가장 가까운 동일 라벨 노드와의 거리가 높은 노드에서도 minority-class에 대한 정확도 감소량이 줄어든 것을 확인할 수 있다. 이러한 부분은 BAT 기법이 논문에서 정의한 AMP와 DMP 수치에 대한 성능 저하를 완화하는 효과가 있음을 보여준다. 그러나 본 논문에서는 다른 기존 기법들이 AMP와 DMP에는 어떻게 영향을 주는지는 제공하고 있지 않아서 다른 기법에 비해서 BAT가 AMP와 DMP를 완화하는 효과가 더 강한지는 알 수가 없다.
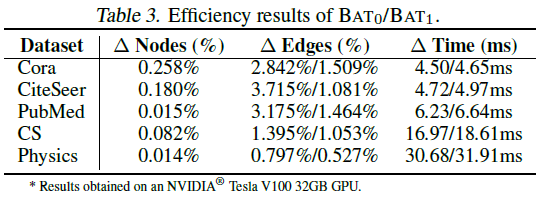
Efficiency
BAT의 최대 단점 중 하나는 학습 과정에서 매 에폭마다 가상 노드와 가상 엣지 생성 과정이 이루어지는 것이 기본이라는 것이다. 물론, 논문에서는 매 에폭마다 진행하지 않고, 가상 노드를 만드는 것을 주기적으로만 해도 된다고 했지만, 성능이 보장될 수 없다는 문제가 있다. 그래서 논문에서도 BAT의 효율성에 대한 부분에 대해서 분석하고, 모델의 효율이 크게 떨어지지 않는다는 점을 강조했다. 아래 표를 통해서 확인할 수 있는 것처럼 실제로 BAT를 수행했을 때, 가상 노드와 연결되는 노드의 수는 극히 소수라는 것을 알 수 있다. 이는 BAT 기법이 매 에폭마다 적용이 되어도 소요 시간이 크게 증가하지 않는다는 것을 보여준다.
5. Conclusion
이 논문에서는 AMP와 DMP라는 개념을 정의하고, 이를 이론적인 측면과 실험적인 측면에서 분석하여 위상적인 불균형이 모델의 학습에 줄 수 있는 영향력을 평가하였다. 그리고 이러한 결과를 기반으로 그래프의 위상 구조를 변경하기 위해서 가상 노드와 가상 엣지를 생성하는 그래프 증강 기법(BAT)을 제시했다.
논문에서 제시한 BAT 기법은 기존 CIGL 기법들과 같이 결합되어 사용될 수 있다는 점에서 장점이 있으며, 실제로 다른 기법과 결합되었을 때 성능을 크게 향상하는데 성공했다. 그러나 BAT의 경우 다른 기법과 다르게 매 에폭마다 수행해야 한다는 점이 가장 큰 단점으로 볼 수 있다. 또한, 이론적인 분석과 실제 BAT 알고리즘 사이 관계가 완전히 논리적으로 정리된 것 같다는 느낌을 주지는 못했다. 증명 과정에서는 이진 분류 시나리오만을 고려하지만, 실제로는 분류군의 개수가 더 많아도 왜 이 알고리즘이 적용 가능한 것인지에 대한 설명이 누락된 점이 보완되었다면 더 좋았을 것 같다.
이 논문에서는 그래프 형태의 데이터가 다른 형태의 데이터와 비교했을 때 갖는 특징을 고려했을 때 발생할 수 있는 시나리오를 깊게 분석하였다. 아마 그러한 부분이 연구의 가치를 더 높였던 것으로 보인다. 그래프 시나리오에서 나올 수 있는 스토리가 새로운 연구 주제로의 가치를 줄 수 있다는 점이 이 논문에서 받은 교훈 중 하나였다.
Author Information
-
안현준 (Hyunjun Ahn)
-
Affiliation: BDI (Big Data Intelligence) Lab
-
Research Topic: Knowledge Graph, Graph Neural Networks
-
Contact: a.hyunjun@kaist.ac.kr
6. Reference & Additional materials
- Link to the Paper
Class-Imbalanced Graph Learning without Class Rebalancing, ICML 2024
- Github Implementation